The method used in the RELIABILITY procedure for computation of approximate pointwise and simultaneous confidence intervals for cumulative failure probabilities relies on the Kaplan-Meier estimator of the cumulative distribution function of failure time and approximate standard deviation of the Kaplan-Meier estimator. For the case of arbitrarily censored data, the Turnbull algorithm, discussed previously, provides an extension of the Kaplan-Meier estimator.

For multiply censored data, the Kaplan-Meier estimator of the cumulative distribution function at failure time is 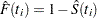, where

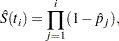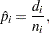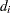is the number of failures in the interval 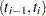, and 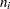is the number of unfailed units at the beginning of the interval. This definition of the Kaplan-Meier estimator is equivalent to the one previously given.

An estimator of the variance 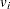of the Kaplan-Meier estimator is given by

An estimator of the standard deviation of is .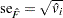

For arbitrarily censored data, the Kaplan-Meier estimator is replaced by the nonparametric maximum likelihood estimator computed with the Turnbull algorithm, and the approximate variance of the estimator of is computed from the inverse of the Fisher information matrix.

Pointwise Confidence Intervals

Approximate pointwise confidence intervals are computed as in Meeker and Escobar (1998, section 3.6) as

where

where is the 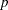th quantile of the standard normal distribution.

Simultaneous Confidence Intervals

Approximate simultaneous confidence bands valid over the lifetime interval 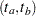are computed as the "Equal Precision" case of Nair (1984) and Meeker and Escobar (1998, section 3.8)

where

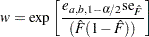where the factor 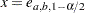is the solution of

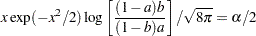The time interval 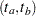over which the bands are valid depends in a complicated way on the constants and defined in Nair (1984), . and are chosen by default, so that the confidence bands are valid between the lowest and highest times corresponding to failures in the case of multiply censored data, or, to the lowest and highest intervals for which probabilities are computed for arbitrarily censored data. You can optionally specify and directly with the NPINTERVALS=SIMULTANEOUS(,) option in the PROBPLOT statement.