| The RELIABILITY Procedure |
| Weibull Analysis of Interval Data with Common Inspection Schedule |
Table 12.1 shows data for 167 identical turbine parts provided by Nelson (1982, p. 415). The parts were inspected at certain times to determine which parts had cracked since the last inspection. The times at which parts develop cracks are to be fitted with a Weibull distribution.
Inspection (Months) |
Number |
||
|---|---|---|---|
Start |
End |
Cracked |
Cumulative |
0 |
6.12 |
5 |
5 |
6.12 |
19.92 |
16 |
21 |
19.92 |
29.64 |
12 |
33 |
29.64 |
35.40 |
18 |
51 |
35.40 |
39.72 |
18 |
69 |
39.72 |
45.24 |
2 |
71 |
45.24 |
52.32 |
6 |
77 |
52.32 |
63.48 |
17 |
94 |
63.48 |
Survived |
73 |
167 |
Table 12.1 shows the time in months of each inspection period and the number of cracked parts found in each period. These data are said to be interval censored since only the time interval in which failures occurred is known, not the exact failure times. Seventy-three parts had not cracked at the last inspection, which took place at 63.48 months. These 73 lifetimes are right censored, since the lifetimes are known only to be greater than 63.48 months.
The interval data in this example are read from a SAS data set with a special structure. All units must have a common inspection schedule. This type of interval data is called readout data. The following SAS program creates the SAS data set named CRACKS, shown in Figure 12.11, and provides the data in Table 12.1 with this structure:
data cracks; input time units fail; datalines; 6.12 167 5 19.92 162 16 29.64 146 12 35.4 134 18 39.72 116 18 45.24 98 2 52.32 96 6 63.48 90 17 ;
The variable Time is the inspection time—that is, the upper endpoint of each interval. The variable Units is the number of unfailed units at the beginning of each interval, and the variable Fail is the number of units with cracks at the inspection time.
The following statements use the RELIABILITY procedure to produce the probability plot in Figure 12.12 for the data in the data set CRACKS:
proc reliability data=cracks;
freq fail;
nenter units;
distribution weibull;
probplot time / readout
ppout
pconfplt
noconf;
run;
The FREQ statement specifies that the variable Fail provides the number of failures in each interval. The NENTER statement specifies that the variable Units provides the number of unfailed units at the beginning of each interval. The DISTRIBUTION statement specifies that the Weibull distribution be used for parameter estimation and probability plotting. The PROBPLOT statement requests a probability plot of the data.
The PROBPLOT statement option READOUT indicates that the data in the CRACKS data set are readout (or interval) data. The option PCONFPLT specifies that confidence intervals for the cumulative probability of failure be plotted. The confidence intervals for the cumulative probability are based on the binomial distribution for time intervals until right censoring occurs. For time intervals after right censoring occurs, the binomial distribution is not valid, and a normal approximation is used to compute confidence intervals.
The option NOCONF suppresses the display of confidence intervals for distribution percentiles in the probability plot.
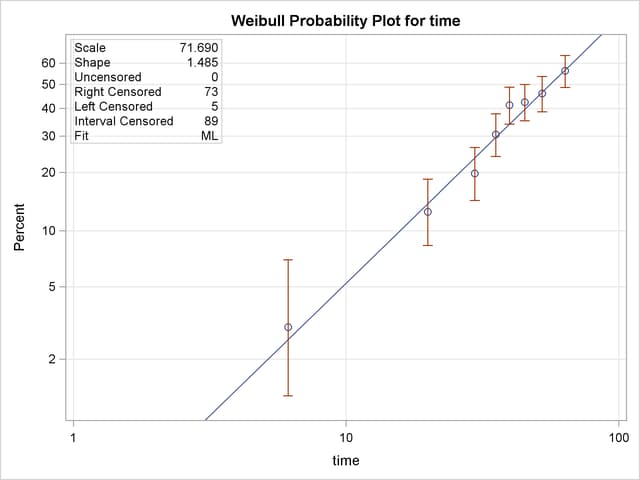
A listing of the tabular output produced by the preceding SAS statements is shown in Figure 12.13 and Figure 12.14. By default, the specified Weibull distribution is fitted by maximum likelihood. The line plotted on the probability plot and the tabular output summarize this fit. For interval data, the estimated cumulative probabilities and associated confidence intervals are tabulated. In addition, general fit information, parameter estimates, percentile estimates, standard errors, and confidence intervals are tabulated.
| Model Information | |
|---|---|
| Input Data Set | WORK.CRACKS |
| Analysis Variable | time |
| Frequency Variable | fail |
| NENTER Variable | units |
| Distribution | Weibull |
| Estimation Method | Maximum Likelihood |
| Confidence Coefficient | 95% |
| Observations Used | 8 |
| Cumulative Probability Estimates | |||||
|---|---|---|---|---|---|
| Lower Lifetime | Upper Lifetime | Cumulative Probability |
Pointwise 95% Confidence Limits |
Standard Error | |
| Lower | Upper | ||||
| . | 6.12 | 0.0299 | 0.0125 | 0.0699 | 0.0132 |
| 6.12 | 19.92 | 0.1257 | 0.0834 | 0.1852 | 0.0257 |
| 19.92 | 29.64 | 0.1976 | 0.1440 | 0.2649 | 0.0308 |
| 29.64 | 35.4 | 0.3054 | 0.2403 | 0.3793 | 0.0356 |
| 35.4 | 39.72 | 0.4132 | 0.3410 | 0.4893 | 0.0381 |
| 39.72 | 45.24 | 0.4251 | 0.3524 | 0.5013 | 0.0383 |
| 45.24 | 52.32 | 0.4611 | 0.3869 | 0.5370 | 0.0386 |
| 52.32 | 63.48 | 0.5629 | 0.4868 | 0.6361 | 0.0384 |
| Weibull Parameter Estimates | ||||
|---|---|---|---|---|
| Parameter | Estimate | Standard Error | Asymptotic Normal | |
| 95% Confidence Limits | ||||
| Lower | Upper | |||
| EV Location | 4.2724 | 0.0744 | 4.1265 | 4.4182 |
| EV Scale | 0.6732 | 0.0664 | 0.5549 | 0.8168 |
| Weibull Scale | 71.6904 | 5.3335 | 61.9634 | 82.9444 |
| Weibull Shape | 1.4854 | 0.1465 | 1.2242 | 1.8022 |
| Other Weibull Distribution Parameters | |
|---|---|
| Parameter | Value |
| Mean | 64.7966 |
| Mode | 33.7622 |
| Median | 56.0144 |
| Standard Deviation | 44.3943 |
| Weibull Percentile Estimates | ||||
|---|---|---|---|---|
| Percent | Estimate | Standard Error | Asymptotic Normal | |
| 95% Confidence Limits | ||||
| Lower | Upper | |||
| 0.1 | 0.68534385 | 0.29999861 | 0.29060848 | 1.61625083 |
| 0.2 | 1.09324674 | 0.42889777 | 0.50673224 | 2.3586193 |
| 0.5 | 2.02798319 | 0.67429625 | 1.05692279 | 3.8912169 |
| 1 | 3.23938972 | 0.93123832 | 1.84401909 | 5.69063837 |
| 2 | 5.18330703 | 1.2581604 | 3.22101028 | 8.34106988 |
| 5 | 9.70579945 | 1.78869256 | 6.76335893 | 13.9283666 |
| 10 | 15.7577991 | 2.22445157 | 11.9491109 | 20.7804776 |
| 20 | 26.1159906 | 2.6327383 | 21.4337103 | 31.821134 |
| 30 | 35.8126238 | 2.90557264 | 30.547517 | 41.9852137 |
| 40 | 45.6100472 | 3.27409792 | 39.6239146 | 52.5005271 |
| 50 | 56.0143651 | 3.89410377 | 48.8792027 | 64.1910859 |
| 60 | 67.5928125 | 4.90210777 | 58.6364803 | 77.917165 |
| 70 | 81.2334227 | 6.46932648 | 69.4938134 | 94.9562075 |
| 80 | 98.7644937 | 8.95137184 | 82.6900902 | 117.963654 |
| 90 | 125.694556 | 13.5078386 | 101.821995 | 155.164133 |
| 95 | 150.057755 | 18.2060035 | 118.300075 | 190.340791 |
| 99 | 200.437864 | 29.1957544 | 150.658574 | 266.66479 |
| 99.9 | 263.348102 | 44.7205513 | 188.791789 | 367.347666 |
In this example, the number of unfailed units at the beginning of an interval minus the number failing in the interval is equal to the number of unfailed units entering the next interval. This is not always the case since some unfailed units might be removed from the test at the end of an interval; that is, they might be right censored. The special structure of the input SAS data set required for interval data enables the RELIABILITY procedure to analyze this more general case.
Copyright © SAS Institute, Inc. All Rights Reserved.