| The CAPABILITY Procedure |
Dictionary of Options
The following entries provide detailed descriptions of options specific to the QQPLOT statement. The notes Traditional Graphics, ODS Graphics, and Line Printer identify options that apply to traditional graphics, ODS Graphics output, and line printers plots, respectively. See Dictionary of Common Options for detailed descriptions of options common to all the plot statements.
- ALPHA=value-list|EST
specifies values for a mandatory shape parameter

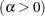 for Q-Q plots requested with the BETA and GAMMA options. A plot is created for each value specified. For examples, see the entries for the BETA and GAMMA options. If you specify ALPHA=EST, a maximum likelihood estimate is computed for
for Q-Q plots requested with the BETA and GAMMA options. A plot is created for each value specified. For examples, see the entries for the BETA and GAMMA options. If you specify ALPHA=EST, a maximum likelihood estimate is computed for  .
. - BETA(ALPHA=value-list|EST BETA=value-list|EST <beta-options>)
creates a beta Q-Q plot for each combination of the shape parameters
 and
and 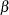 given by the mandatory ALPHA= and BETA= options. If you specify ALPHA=EST and BETA=EST, a plot is created based on maximum likelihood estimates for
given by the mandatory ALPHA= and BETA= options. If you specify ALPHA=EST and BETA=EST, a plot is created based on maximum likelihood estimates for  and
and 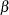 . In the following example, the first QQPLOT statement produces one plot, the second statement produces four plots, the third statement produces six plots, and the fourth statement produces one plot:
. In the following example, the first QQPLOT statement produces one plot, the second statement produces four plots, the third statement produces six plots, and the fourth statement produces one plot: proc capability data=measures; qqplot width / beta(alpha=2 beta=2); qqplot width / beta(alpha=2 3 beta=1 2); qqplot width / beta(alpha=2 to 3 beta=1 to 2 by 0.5); qqplot width / beta(alpha=est beta=est); run;
To create the plot, the observations are ordered from smallest to largest, and the
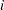 th ordered observation is plotted against the quantile
th ordered observation is plotted against the quantile 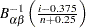 , where
, where 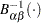 is the inverse normalized incomplete beta function,
is the inverse normalized incomplete beta function,  is the number of nonmissing observations, and
is the number of nonmissing observations, and  and
and 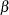 are the shape parameters of the beta distribution.
are the shape parameters of the beta distribution. The point pattern on the plot for ALPHA=
 and BETA=
and BETA=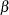 tends to be linear with intercept
tends to be linear with intercept 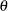 and slope
and slope  if the data are beta distributed with the specific density function
if the data are beta distributed with the specific density function 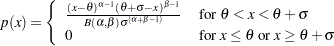
where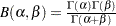 , and
, and 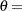 lower threshold parameter
lower threshold parameter 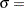 scale parameter
scale parameter 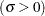
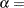 first shape parameter
first shape parameter 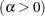
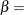 second shape parameter
second shape parameter 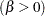
To obtain graphical estimates of
 and
and 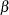 , specify lists of values for the ALPHA= and BETA= options, and select the combination of
, specify lists of values for the ALPHA= and BETA= options, and select the combination of  and
and 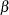 that most nearly linearizes the point pattern. To assess the point pattern, you can add a diagonal distribution reference line with intercept
that most nearly linearizes the point pattern. To assess the point pattern, you can add a diagonal distribution reference line with intercept  and slope
and slope  with the beta-options THETA=
with the beta-options THETA= and SIGMA=
and SIGMA= . Alternatively, you can add a line corresponding to estimated values of
. Alternatively, you can add a line corresponding to estimated values of  and slope
and slope  with the beta-options THETA=EST and SIGMA=EST. Specify these options in parentheses, as in the following example:
with the beta-options THETA=EST and SIGMA=EST. Specify these options in parentheses, as in the following example: proc capability data=measures; qqplot width / beta(alpha=2 beta=3 theta=4 sigma=5); run;
Agreement between the reference line and the point pattern indicates that the beta distribution with parameters
 ,
, 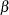 ,
,  , and
, and  is a good fit. You can specify the SCALE= option as an alias for the SIGMA= option and the THRESHOLD= option as an alias for the THETA= option.
is a good fit. You can specify the SCALE= option as an alias for the SIGMA= option and the THRESHOLD= option as an alias for the THETA= option. - BETA=value-list|EST
specifies values for the shape parameter
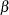
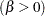 for Q-Q plots requested with the BETA distribution option. A plot is created for each value specified with the BETA= option. If you specify BETA=EST, a maximum likelihood estimate is computed for
for Q-Q plots requested with the BETA distribution option. A plot is created for each value specified with the BETA= option. If you specify BETA=EST, a maximum likelihood estimate is computed for 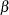 . For examples, see the preceding entry for the BETA distribution option.
. For examples, see the preceding entry for the BETA distribution option. - C=value(-list)|EST
specifies the shape parameter

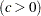 for Q-Q plots requested with the WEIBULL and WEIBULL2 options. You must specify C= as a Weibull-option with the WEIBULL option; in this situation it accepts a list of values, or if you specify C=EST, a maximum likelihood estimate is computed for
for Q-Q plots requested with the WEIBULL and WEIBULL2 options. You must specify C= as a Weibull-option with the WEIBULL option; in this situation it accepts a list of values, or if you specify C=EST, a maximum likelihood estimate is computed for  . You can optionally specify C=value or C=EST as a Weibull2-option with the WEIBULL2 option to request a distribution reference line; in this situation, you must also specify SIGMA=value or SIGMA=EST. For an example, see Output 5.23.1.
. You can optionally specify C=value or C=EST as a Weibull2-option with the WEIBULL2 option to request a distribution reference line; in this situation, you must also specify SIGMA=value or SIGMA=EST. For an example, see Output 5.23.1. - CGRID=color
[Traditional Graphics] specifies the color for the grid lines associated with the quantile axis, requested by the GRID option.
- CPKREF
[Traditional Graphics] draws reference lines extending from the intersections of the specification limits with the distribution reference line to the quantile axis in plots requested with the NORMAL option. Specify CPKREF in parentheses after the NORMAL option. You can use the CPKREF option with the CPKSCALE option for graphical estimation of the capability indices CPU, CPL, and
 , as illustrated in Output 5.24.1.
, as illustrated in Output 5.24.1. - CPKSCALE
rescales the quantile axis in
 units for plots requested with the NORMAL option. Specify CPKSCALE in parentheses after the NORMAL option. You can use the CPKSCALE option with the CPKREF option for graphical estimation of the capability indices CPU, CPL, and
units for plots requested with the NORMAL option. Specify CPKSCALE in parentheses after the NORMAL option. You can use the CPKSCALE option with the CPKREF option for graphical estimation of the capability indices CPU, CPL, and  , as illustrated in Output 5.24.1.
, as illustrated in Output 5.24.1. - EXPONENTIAL(<(exponential-options)>
- EXP<(exponential-options)>)
creates an exponential Q-Q plot. To create the plot, the observations are ordered from smallest to largest, and the
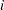 th ordered observation is plotted against the quantile
th ordered observation is plotted against the quantile 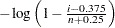 , where
, where  is the number of nonmissing observations.
is the number of nonmissing observations. The pattern on the plot tends to be linear with intercept
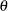 and slope
and slope  if the data are exponentially distributed with the specific density function
if the data are exponentially distributed with the specific density function 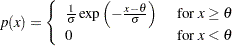
where
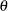 is the threshold parameter, and
is the threshold parameter, and  is the scale parameter
is the scale parameter 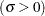 .
. To assess the point pattern, you can add a diagonal distribution reference line with intercept
 and slope
and slope  with the exponential-options THETA=
with the exponential-options THETA= and SIGMA=
and SIGMA= . Alternatively, you can add a line corresponding to estimated values of
. Alternatively, you can add a line corresponding to estimated values of  and slope
and slope  with the exponential-options THETA=EST and SIGMA=EST. Specify these options in parentheses, as in the following example: as in the following example:
with the exponential-options THETA=EST and SIGMA=EST. Specify these options in parentheses, as in the following example: as in the following example: proc capability data=measures; qqplot width / exponential(theta=4 sigma=5); run;
Agreement between the reference line and the point pattern indicates that the exponential distribution with parameters
 and
and  is a good fit. You can specify the SCALE= option as an alias for the SIGMA= option and the THRESHOLD= option as an alias for the THETA= option.
is a good fit. You can specify the SCALE= option as an alias for the SIGMA= option and the THRESHOLD= option as an alias for the THETA= option. - GAMMA(ALPHA=value-list|EST <gamma-options> )
creates a gamma Q-Q plot for each value of the shape parameter
 given by the mandatory ALPHA= option or its alias, the SHAPE= option. The following example produces three probability plots:
given by the mandatory ALPHA= option or its alias, the SHAPE= option. The following example produces three probability plots: proc capability data=measures; qqplot width / gamma(alpha=0.4 to 0.6 by 0.1); run;
To create the plot, the observations are ordered from smallest to largest, and the
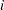 th ordered observation is plotted against the quantile
th ordered observation is plotted against the quantile 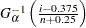 , where
, where 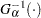 is the inverse normalized incomplete gamma function,
is the inverse normalized incomplete gamma function,  is the number of nonmissing observations, and
is the number of nonmissing observations, and  is the shape parameter of the gamma distribution.
is the shape parameter of the gamma distribution. The pattern on the plot for ALPHA=
 tends to be linear with intercept
tends to be linear with intercept 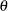 and slope
and slope  if the data are gamma distributed with the specific density function
if the data are gamma distributed with the specific density function 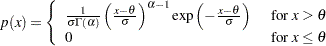
where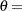 threshold parameter
threshold parameter 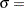 scale parameter
scale parameter 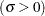
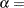 shape parameter
shape parameter 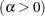
To obtain a graphical estimate of
 , specify a list of values for the ALPHA= option, and select the value that most nearly linearizes the point pattern.
, specify a list of values for the ALPHA= option, and select the value that most nearly linearizes the point pattern. To assess the point pattern, you can add a diagonal distribution reference line with intercept
 and slope
and slope  with the gamma-options THETA=
with the gamma-options THETA= and SIGMA=
and SIGMA= . Alternatively, you can add a line corresponding to estimated values of
. Alternatively, you can add a line corresponding to estimated values of  and
and  with the gamma-options THETA=EST and SIGMA=EST. Specify these options in parentheses, as in the following example:
with the gamma-options THETA=EST and SIGMA=EST. Specify these options in parentheses, as in the following example: proc capability data=measures; qqplot width / gamma(alpha=2 theta=3 sigma=4); run;
Agreement between the reference line and the point pattern indicates that the gamma distribution with parameters
 ,
,  , and
, and  is a good fit. You can specify the SCALE= option as an alias for the SIGMA= option and the THRESHOLD= option as an alias for the THETA= option.
is a good fit. You can specify the SCALE= option as an alias for the SIGMA= option and the THRESHOLD= option as an alias for the THETA= option. - GRID
draws reference lines perpendicular to the quantile axis at major tick marks.
- LEGEND=name | NONE
specifies the name of a LEGEND statement describing the legend for specification limit reference lines and fitted curves. Specifying LEGEND=NONE is equivalent to specifying the NOLEGEND option.
- LGRID=linetype
[Traditional Graphics] specifies the line type for the grid lines associated with the quantile axis, requested by the GRID option.
- LOGNORMAL(SIGMA=value-list|EST <lognormal-options>)
- LNORM(SIGMA=value-list|EST <lognormal-options>)
creates a lognormal Q-Q plot for each value of the shape parameter
 given by the mandatory SIGMA= option or its alias, the SHAPE= option. For example,
given by the mandatory SIGMA= option or its alias, the SHAPE= option. For example, proc capability data=measures; qqplot width/ lognormal(shape=1.5 2.5); run;
To create the plot, the observations are ordered from smallest to largest, and the
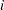 th ordered observation is plotted against the quantile
th ordered observation is plotted against the quantile 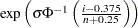 , where
, where 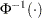 is the inverse cumulative standard normal distribution,
is the inverse cumulative standard normal distribution,  is the number of nonmissing observations, and
is the number of nonmissing observations, and  is the shape parameter of the lognormal distribution.
is the shape parameter of the lognormal distribution. The pattern on the plot for SIGMA=
 tends to be linear with intercept
tends to be linear with intercept 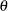 and slope
and slope 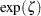 if the data are lognormally distributed with the specific density function
if the data are lognormally distributed with the specific density function 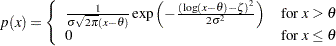
where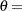 threshold parameter
threshold parameter 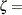 scale parameter
scale parameter 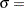 shape parameter
shape parameter 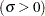
To obtain a graphical estimate of
 , specify a list of values for the SIGMA= option, and select the value that most nearly linearizes the point pattern. For an illustration, see Example 5.22.
, specify a list of values for the SIGMA= option, and select the value that most nearly linearizes the point pattern. For an illustration, see Example 5.22. To assess the point pattern, you can add a diagonal distribution reference line corresponding to the threshold parameter
 and the scale parameter
and the scale parameter 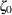 with the lognormal-options THETA=
with the lognormal-options THETA= and ZETA=
and ZETA=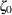 . Alternatively, you can add a line corresponding to estimated values of
. Alternatively, you can add a line corresponding to estimated values of  and
and 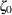 with the lognormal-options THETA=EST and ZETA=EST. This line has intercept
with the lognormal-options THETA=EST and ZETA=EST. This line has intercept  and slope
and slope 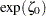 . Agreement between the line and the point pattern indicates that the lognormal distribution with parameters
. Agreement between the line and the point pattern indicates that the lognormal distribution with parameters  ,
,  , and
, and 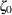 is a good fit. See Output 5.22.4 for an example. You can specify the THRESHOLD= option as an alias for the THETA= option and the SCALE= option as an alias for the ZETA= option.
is a good fit. See Output 5.22.4 for an example. You can specify the THRESHOLD= option as an alias for the THETA= option and the SCALE= option as an alias for the ZETA= option. You can also display the reference line by specifying THETA=
 , and you can specify the slope with the SLOPE= option. For example, the following two QQPLOT statements produce charts with identical reference lines:
, and you can specify the slope with the SLOPE= option. For example, the following two QQPLOT statements produce charts with identical reference lines: proc capability data=measures; qqplot width / lognormal(sigma=2 theta=3 zeta=1); qqplot width / lognormal(sigma=2 theta=3 slope=2.718); run;
- MU=value|EST
specifies a value for the mean
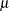 for a normal Q-Q plot requested with the NORMAL option. Specify MU=
for a normal Q-Q plot requested with the NORMAL option. Specify MU=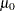 and SIGMA=
and SIGMA= to request a distribution reference line with intercept
to request a distribution reference line with intercept 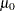 and slope
and slope  . Specify MU=EST to request a distribution reference line with intercept equal to the sample mean, as illustrated in Figure 5.20.3.
. Specify MU=EST to request a distribution reference line with intercept equal to the sample mean, as illustrated in Figure 5.20.3. - NADJ=value
specifies the adjustment value added to the sample size in the calculation of theoretical quantiles. The default is
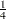 , as described by Blom (1958). Also refer to Chambers et al. (1983) for additional information.
, as described by Blom (1958). Also refer to Chambers et al. (1983) for additional information. - NOLEGEND
- LEGEND=NONE
suppresses legends for specification limits, fitted curves, distribution lines, and hidden observations. For an example, see Output 5.24.1.
- NOLINELEGEND
- NOLINEL
suppresses the legend for the optional distribution reference line.
- NOOBSLEGEND
- NOOBSL
[Line Printer] suppresses the legend that indicates the number of hidden observations.
- NORMAL<(normal-options)>
- NORM<(normal-options)>
creates a normal Q-Q plot. This is the default if you do not specify a distribution option. To create the plot, the observations are ordered from smallest to largest, and the
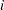 th ordered observation is plotted against the quantile
th ordered observation is plotted against the quantile 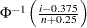 , where
, where 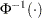 is the inverse cumulative standard normal distribution, and
is the inverse cumulative standard normal distribution, and  is the number of nonmissing observations.
is the number of nonmissing observations. The pattern on the plot tends to be linear with intercept
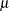 and slope
and slope  if the data are normally distributed with the specific density function
if the data are normally distributed with the specific density function 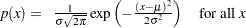
where
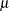 is the mean, and
is the mean, and  is the standard deviation
is the standard deviation 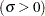 .
. To assess the point pattern, you can add a diagonal distribution reference line with intercept
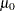 and slope
and slope  with the normal-options MU=
with the normal-options MU=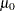 and SIGMA=
and SIGMA= . Alternatively, you can add a line corresponding to estimated values of
. Alternatively, you can add a line corresponding to estimated values of 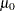 and
and  with the normal-options THETA=EST and SIGMA=EST; the estimates of
with the normal-options THETA=EST and SIGMA=EST; the estimates of 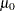 and
and 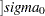 are the sample mean and sample standard deviation. Specify these options in parentheses, as in the following example:
are the sample mean and sample standard deviation. Specify these options in parentheses, as in the following example: proc capability data=measures; qqplot length / normal(mu=10 sigma=0.3); run;
For an example, see Adding a Distribution Reference Line. Agreement between the reference line and the point pattern indicates that the normal distribution with parameters
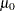 and
and  is a good fit. You can specify MU=EST and SIGMA=EST to request a distribution reference line with the sample mean and sample standard deviation as the intercept and slope.
is a good fit. You can specify MU=EST and SIGMA=EST to request a distribution reference line with the sample mean and sample standard deviation as the intercept and slope. Other normal-options include CPKREF and CPKSCALE. The CPKREF option draws reference lines extending from the intersections of specification limits with the distribution reference line to the theoretical quantile axis. The CPKSCALE option rescales the theoretical quantile axis in
 units. You can use the CPKREF option with the CPKSCALE option for graphical estimation of the capability indices CPU, CPL, and
units. You can use the CPKREF option with the CPKSCALE option for graphical estimation of the capability indices CPU, CPL, and  , as illustrated in Output 5.24.1.
, as illustrated in Output 5.24.1. - NOSPECLEGEND
- NOSPECL
suppresses the legend for specification limit reference lines. For an example, see Figure 5.20.3.
- PCTLAXIS(axis-options)
adds a nonlinear percentile axis along the frame of the Q-Q plot opposite the theoretical quantile axis. The added axis is identical to the axis for probability plots produced with the PROBPLOT statement. When using the PCTLAXIS option, you must specify HREF= values in quantile units, and you cannot use the NOFRAME option. You can specify the following axis-options:
- CGRID=color
specifies the color used for grid lines.
- GRID
draws grid lines perpindicular to the percentile axis at major tick marks.
- GRIDCHAR='character'
specifies the character used to draw grid lines associated with the percentile axis on line printer plots.
- LABEL='string'
specifies the label for the percentile axis.
- LGRID=linetype
specifies the line type used for grid lines associated with the percentile axis.
- WGRID=value
specifies the thickness for grid lines associated with the percentile axis.
[See CAPQQ1 in the SAS/QC Sample Library]For example, the following statements display the plot in Figure 5.20.4:
symbol v=plus; title 'Normal Quantile-Quantile Plot for Hole Distance'; proc capability data=Sheets noprint; qqplot Distance / normal(mu=est sigma=est color=black) nolegend pctlaxis(grid lgrid=35 label='Normal Percentiles'); run;Output 5.20.4 Normal Q-Q Plot with Percentile Axis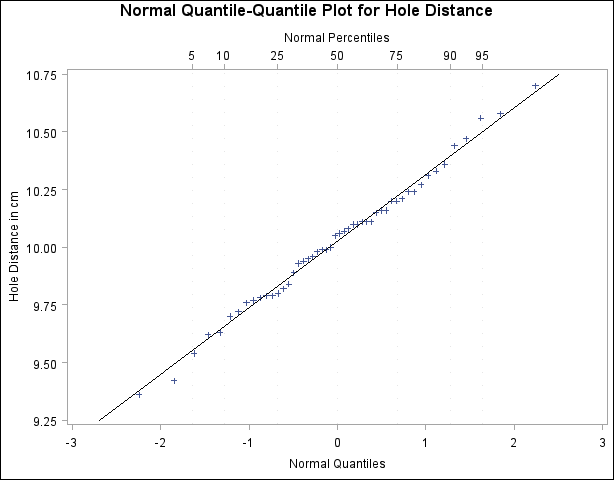
- PCTLMINOR
requests minor tick marks for the percentile axis displayed when you use the PCTLAXIS option. See the entry for the PCTLAXIS option for an example.
- PCTLSCALE
requests scale labels for the theoretical quantile axis in percentile units, resulting in a nonlinear axis scale. Tick marks are drawn uniformly across the axis based on the quantile scale. In all other respects, the plot remains the same, and you must specify HREF= values in quantile units. For a true nonlinear axis, use the PCTLAXIS option or use the PROBPLOT statement. For example, the following statements display the plot in Figure 5.20.5:
[See CAPQQ1 in the SAS/QC Sample Library]
symbol v=plus; title 'Normal Quantile-Quantile Plot for Hole Distance'; proc capability data=Sheets noprint; spec lsl=9.5 usl=10.5; qqplot Distance / normal(mu=est sigma=est cpkref) pctlaxis(grid lgrid=35) nolegend pctlscale; run;Output 5.20.5 Normal Q-Q Plot for Reading Percentiles of Specification Limits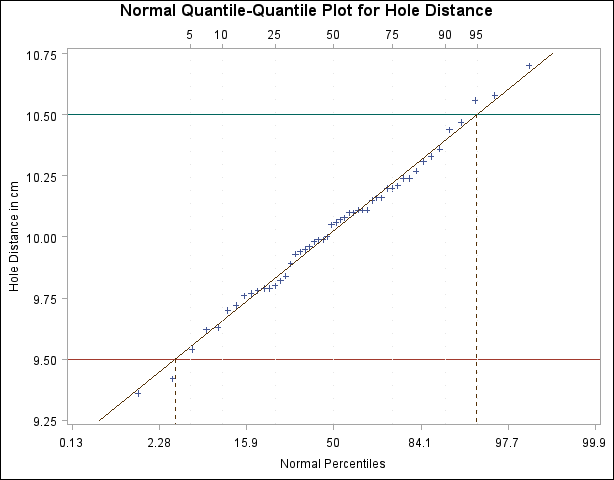
- QQSYMBOL='character'
[Line Printer] specifies the character used to plot the Q-Q points in line printer plots. The default is the plus sign (
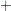 ).
). - RANKADJ=value
specifies the adjustment value added to the ranks in the calculation of theoretical quantiles. The default is
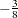 , as described by Blom (1958). Also refer to Chambers et al. (1983) for additional information.
, as described by Blom (1958). Also refer to Chambers et al. (1983) for additional information. - ROTATE
switches the horizontal and vertical axes so that the theoretical percentiles are plotted vertically while the data are plotted horizontally. Regardless of whether the plot has been rotated, horizontal axis options (such as HAXIS=) refer to the horizontal axis, and vertical axis options (such as VAXIS=) refer to the vertical axis. All other options that depend on axis placement adjust to the rotated axes.
- SIGMA=value-list|EST
specifies the value of the distribution parameter
 , where
, where 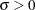 . Alternatively, you can specify SIGMA=EST to request a maximum likelihood estimate for
. Alternatively, you can specify SIGMA=EST to request a maximum likelihood estimate for  . The use of the SIGMA= option depends on the distribution option specified, as indicated by the following table:
. The use of the SIGMA= option depends on the distribution option specified, as indicated by the following table: Distribution Option
Use of the SIGMA= Option
THETA=
 and SIGMA=
and SIGMA= request a distribution reference
request a distribution reference line with intercept
 and slope
and slope  .
. SIGMA=
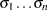 requests
requests  Q-Q plots with shape parameters
Q-Q plots with shape parameters 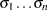 . The SIGMA= option is mandatory.
. The SIGMA= option is mandatory. MU=
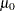 and SIGMA=
and SIGMA= request a distribution reference line with intercept
request a distribution reference line with intercept 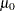 and slope
and slope  . SIGMA=EST requests a slope equal to the sample standard deviation.
. SIGMA=EST requests a slope equal to the sample standard deviation. SIGMA=
 and C=
and C=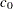 request a distribution reference line with intercept
request a distribution reference line with intercept 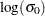 and slope
and slope 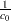 .
. For an example using SIGMA=EST, see Output 5.24.1. For an example of lognormal plots using the SIGMA= option, see Example 5.22.
- SLOPE=value|EST
specifies the slope for a distribution reference line requested with the LOGNORMAL and WEIBULL2 options.
When you use the SLOPE= option with the LOGNORMAL option, you must also specify a threshold parameter value
 with the THETA= option. Specifying the SLOPE= option is an alternative to specifying ZETA=
with the THETA= option. Specifying the SLOPE= option is an alternative to specifying ZETA=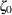 , which requests a slope of
, which requests a slope of 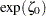 . See Output 5.22.4 for an example.
. See Output 5.22.4 for an example. When you use the SLOPE= option with the WEIBULL2 option, you must also specify a scale parameter value
 with the SIGMA= option. Specifying the SLOPE= option is an alternative to specifying C=
with the SIGMA= option. Specifying the SLOPE= option is an alternative to specifying C=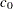 , which requests a slope of
, which requests a slope of 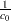 .
. For example, the first and second QQPLOT statements that follow produce plots identical to those produced by the third and fourth QQPLOT statements:
proc capability data=measures; qqplot width / lognormal(sigma=2 theta=0 zeta=0); qqplot width / weibull2(sigma=2 theta=0 c=0.25); qqplot width / lognormal(sigma=2 theta=0 slope=1); qqplot width / weibull2(sigma=2 theta=0 slope=4); run;
For more information, see Graphical Estimation.
- SQUARE
[Traditional Graphics][ODS Graphics] displays the Q-Q plot in a square frame. Compare Figure 5.20.2 with Figure 5.20.3. The default is a rectangular frame.
- SYMBOL='character'
[Line Printer] specifies the character used for a distribution reference line in a line printer plot. The default character is the first letter of the distribution option keyword.
- THETA=value|EST
specifies the lower threshold parameter
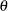 for Q-Q plots requested with the BETA, EXPONENTIAL, GAMMA, LOGNORMAL, WEIBULL, and WEIBULL2 options.
for Q-Q plots requested with the BETA, EXPONENTIAL, GAMMA, LOGNORMAL, WEIBULL, and WEIBULL2 options. When used with the WEIBULL2 option, the THETA= option specifies the known lower threshold
 , for which the default is 0. See Output 5.23.2 for an example.
, for which the default is 0. See Output 5.23.2 for an example. When used with the other distribution options, the THETA= option specifies
 for a distribution reference line; alternatively in this situation, you can specify THETA=EST to request a maximum likelihood estimate for
for a distribution reference line; alternatively in this situation, you can specify THETA=EST to request a maximum likelihood estimate for  . To request the line, you must also specify a scale parameter See Output 5.22.4 for an example of the THETA= option with a lognormal Q-Q plot.
. To request the line, you must also specify a scale parameter See Output 5.22.4 for an example of the THETA= option with a lognormal Q-Q plot. - THRESHOLD=value|EST
- WEIBULL(C=value-list|EST <Weibull-options>)
- WEIB(C=value-list <Weibull-options>)
creates a three-parameter Weibull Q-Q plot for each value of the shape parameter
 given by the mandatory C= option or its alias, the SHAPE= option. For example,
given by the mandatory C= option or its alias, the SHAPE= option. For example, proc capability data=measures; qqplot width / weibull(c=1.8 to 2.4 by 0.2); run;
To create the plot, the observations are ordered from smallest to largest, and the
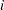 th ordered observation is plotted against the quantile
th ordered observation is plotted against the quantile 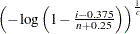 , where
, where  is the number of nonmissing observations, and
is the number of nonmissing observations, and  is the Weibull distribution shape parameter.
is the Weibull distribution shape parameter. The pattern on the plot for C=
 tends to be linear with intercept
tends to be linear with intercept 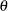 and slope
and slope  if the data are Weibull distributed with the specific density function
if the data are Weibull distributed with the specific density function 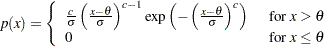
where
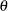 is the threshold parameter,
is the threshold parameter,  is the scale parameter
is the scale parameter 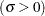 , and
, and  is the shape parameter
is the shape parameter 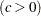 .
. To obtain a graphical estimate of
 , specify a list of values for the C= option, and select the value that most nearly linearizes the point pattern. For an illustration, see Example 5.23. To assess the point pattern, you can add a diagonal distribution reference line with intercept
, specify a list of values for the C= option, and select the value that most nearly linearizes the point pattern. For an illustration, see Example 5.23. To assess the point pattern, you can add a diagonal distribution reference line with intercept  and slope
and slope  with the Weibull-options THETA=
with the Weibull-options THETA= and SIGMA=
and SIGMA= . Alternatively, you can add a line corresponding to estimated values of
. Alternatively, you can add a line corresponding to estimated values of  and
and  with the Weibull-options THETA=EST and SIGMA=EST. Specify these options in parentheses, as in the following example:
with the Weibull-options THETA=EST and SIGMA=EST. Specify these options in parentheses, as in the following example: proc capability data=measures; qqplot width / weibull(c=2 theta=3 sigma=4); run;
Agreement between the reference line and the point pattern indicates that the Weibull distribution with parameters
 ,
,  , and
, and  is a good fit. You can specify the SCALE= option as an alias for the SIGMA= option and the THRESHOLD= option as an alias for the THETA= option.
is a good fit. You can specify the SCALE= option as an alias for the SIGMA= option and the THRESHOLD= option as an alias for the THETA= option. - WEIBULL2<(Weibull2-options)>
- W2<(Weibull2-options)>
creates a two-parameter Weibull Q-Q plot. You should use the WEIBULL2 option when your data have a known lower threshold
 . You can specify the threshold value
. You can specify the threshold value  with the THETA= option or its alias, the THRESHOLD= option. If you are uncertain of the lower threshold value, you can estimate
with the THETA= option or its alias, the THRESHOLD= option. If you are uncertain of the lower threshold value, you can estimate  graphically by specifying a list of values for the THETA= option. Select the value that most linearizes the point pattern. The default is
graphically by specifying a list of values for the THETA= option. Select the value that most linearizes the point pattern. The default is 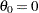 .
. To create the plot, the observations are ordered from smallest to largest, and the log of the shifted
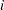 th ordered observation
th ordered observation 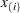 ,
, 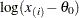 , is plotted against the quantile
, is plotted against the quantile 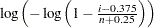 , where
, where  is the number of nonmissing observations. Unlike the three-parameter Weibull quantile, the preceding expression is free of distribution parameters. This is why the C= shape parameter option is not mandatory with the WEIBULL2 option.
is the number of nonmissing observations. Unlike the three-parameter Weibull quantile, the preceding expression is free of distribution parameters. This is why the C= shape parameter option is not mandatory with the WEIBULL2 option. The pattern on the plot for THETA=
 tends to be linear with intercept
tends to be linear with intercept 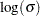 and slope
and slope  if the data are Weibull distributed with the specific density function
if the data are Weibull distributed with the specific density function 
where
 is a known lower threshold parameter,
is a known lower threshold parameter,  is a scale parameter
is a scale parameter 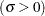 , and
, and  is a shape parameter
is a shape parameter 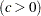 .
. The advantage of a two-parameter Weibull plot over a three-parameter Weibull plot is that you can visually estimate the shape parameter
 and the scale parameter
and the scale parameter  from the slope and intercept of the point pattern; see Example 5.23 for an illustration of this method. The disadvantage is that the two-parameter Weibull distribution applies only in situations where the threshold parameter is known. See Graphical Estimation for more information.
from the slope and intercept of the point pattern; see Example 5.23 for an illustration of this method. The disadvantage is that the two-parameter Weibull distribution applies only in situations where the threshold parameter is known. See Graphical Estimation for more information. To assess the point pattern, you can add a diagonal distribution reference line corresponding to the scale parameter
 and shape parameter
and shape parameter 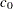 with the Weibull2-options SIGMA=
with the Weibull2-options SIGMA= and C=
and C=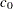 . Alternatively, you can add a distribution reference line corresponding to estimated values of
. Alternatively, you can add a distribution reference line corresponding to estimated values of  and
and 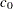 with the Weibull2-options SIGMA=EST and C=EST. This line has intercept
with the Weibull2-options SIGMA=EST and C=EST. This line has intercept 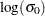 and slope
and slope 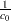 . Agreement between the line and the point pattern indicates that the Weibull distribution with parameters
. Agreement between the line and the point pattern indicates that the Weibull distribution with parameters 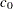 ,
,  , and
, and  is a good fit. You can specify the SCALE= option as an alias for the SIGMA= option and the SHAPE= option as an alias for the C= option.
is a good fit. You can specify the SCALE= option as an alias for the SIGMA= option and the SHAPE= option as an alias for the C= option. You can also display the reference line by specifying SIGMA=
 , and you can specify the slope with the SLOPE= option. For example, the following QQPLOT statements produce identical plots:
, and you can specify the slope with the SLOPE= option. For example, the following QQPLOT statements produce identical plots: proc capability data=measures; qqplot width / weibull2(theta=3 sigma=4 c=2); qqplot width / weibull2(theta=3 sigma=4 slope=0.5); run;
-
WGRID=

[Traditional Graphics] specifies the width of the grid lines associated with the quantile axis, requested with the GRID option. If you use the WGRID= option, you do not need to specify the GRID option.
- ZETA=value|EST
specifies a value for the scale parameter
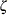 for lognormal Q-Q plots requested with the LOGNORMAL option. Specify THETA=
for lognormal Q-Q plots requested with the LOGNORMAL option. Specify THETA= and ZETA=
and ZETA=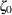 to request a distribution reference line with intercept
to request a distribution reference line with intercept  and slope
and slope 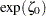 .
.
Copyright © SAS Institute, Inc. All Rights Reserved.