The FREQ Procedure
The odds ratio is a useful measure of association for a variety of study designs. For a retrospective design called a case-control study, the odds ratio can be used to estimate the relative risk when the probability of positive response is small (Agresti, 2002). In a case-control study, two independent samples are identified based on a binary (yes-no) response variable, and the conditional distribution of a binary explanatory variable is examined, within fixed levels of the response variable. See Stokes, Davis, and Koch (2012) and Agresti (2007).
The odds of a positive response (column 1) in row 1 is ![]() . Similarly, the odds of a positive response in row 2 is
. Similarly, the odds of a positive response in row 2 is ![]() . The odds ratio is formed as the ratio of the row 1 odds to the row 2 odds. The odds ratio for a
. The odds ratio is formed as the ratio of the row 1 odds to the row 2 odds. The odds ratio for a ![]() table is defined as
table is defined as
The odds ratio can be any nonnegative number. When the row and column variables are independent, the true value of the odds ratio equals 1. An odds ratio greater than 1 indicates that the odds of a positive response are higher in row 1 than in row 2. Values less than 1 indicate the odds of positive response are higher in row 2. The strength of association increases with the deviation from 1.
The transformation ![]() transforms the odds ratio to the range (–1,1) with G = 0 when
transforms the odds ratio to the range (–1,1) with G = 0 when ![]() ; G = –1 when
; G = –1 when ![]() ; and G approaches 1 as OR approaches infinity. G is the gamma statistic, which PROC FREQ computes when you specify the MEASURES option.
; and G approaches 1 as OR approaches infinity. G is the gamma statistic, which PROC FREQ computes when you specify the MEASURES option.
The asymptotic ![]() % confidence limits for the odds ratio are
% confidence limits for the odds ratio are
where
and z is the ![]() percentile of the standard normal distribution. If any of the four cell frequencies are zero, the estimates are not computed.
percentile of the standard normal distribution. If any of the four cell frequencies are zero, the estimates are not computed.
Score confidence limits for the odds ratio (Miettinen and Nurminen, 1985) are computed by inverting score tests for the odds ratio. A score-based chi-square test statistic for the null hypothesis that the odds ratio equals ![]() can be expressed as
can be expressed as
where ![]() is the observed row 1 risk (proportion), and
is the observed row 1 risk (proportion), and ![]() and
and ![]() are the maximum likelihood estimates of the row 1 and row 2 risks under the restriction that the odds ratio (
are the maximum likelihood estimates of the row 1 and row 2 risks under the restriction that the odds ratio (![]() ) is
) is ![]() . For more information, see Miettinen and Nurminen (1985) and Miettinen (1985, chapter 14).
. For more information, see Miettinen and Nurminen (1985) and Miettinen (1985, chapter 14).
The ![]() % score confidence interval for the odds ratio consists of all values of
% score confidence interval for the odds ratio consists of all values of ![]() for which the test statistic
for which the test statistic ![]() falls in the acceptance region,
falls in the acceptance region,
where ![]() is the 100
is the 100![]() percentile of the chi-square distribution with one degree of freedom. PROC FREQ finds the confidence limits by iterative
computation. For more information about score confidence limits, see Agresti (2013).
percentile of the chi-square distribution with one degree of freedom. PROC FREQ finds the confidence limits by iterative
computation. For more information about score confidence limits, see Agresti (2013).
By default, the score confidence limits include the bias correction factor ![]() in the denominator of
in the denominator of ![]() (Miettinen and Nurminen, 1985, p. 217). If you specify the CL=SCORE(CORRECT=NO) option, PROC FREQ does not include this factor in the computation.
(Miettinen and Nurminen, 1985, p. 217). If you specify the CL=SCORE(CORRECT=NO) option, PROC FREQ does not include this factor in the computation.
The maximum likelihood estimates of ![]() and
and ![]() , subject to the constraint that the odds ratio is
, subject to the constraint that the odds ratio is ![]() , are computed as
, are computed as
where
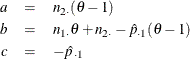
For more information, see Miettinen and Nurminen (1985, pp. 217–218) and Miettinen (1985, chapter 14).
When you specify the OR option in the EXACT statement, PROC FREQ computes exact confidence limits for the odds ratio. Because
this is a discrete problem, the confidence coefficient for the exact confidence interval is not exactly ![]() but is at least
but is at least ![]() . Thus, these confidence limits are conservative. See Agresti (1992) for more information.
. Thus, these confidence limits are conservative. See Agresti (1992) for more information.
PROC FREQ computes exact confidence limits for the odds ratio by using an algorithm based on Thomas (1971). See also Gart (1971). The following two equations are solved iteratively to determine the lower and upper confidence limits, ![]() and
and ![]() :
:
![\begin{eqnarray*} \sum _{i=n_{11}}^{n_{\cdot 1}} \binom {n_{1 \cdot }}{i} \binom {n_{2 \cdot }}{n_{\cdot 1} - i} ~ \phi _1^ i ~ ~ / ~ ~ \sum _{i=0}^{n_{\cdot 1}} \binom {n_{1 \cdot }}{i} \binom {n_{2 \cdot }}{n_{\cdot 1}-i} ~ \phi _1^ i ~ & = & ~ \alpha /2 \\[0.10in] \sum _{i=0}^{n_{11}} \binom {n_{1 \cdot }}{i} \binom {n_{2 \cdot }}{n_{\cdot 1} - i} ~ \phi _2^ i ~ ~ / ~ ~ \sum _{i=0}^{n_{\cdot 1}} \binom {n_{1 \cdot }}{i} \binom {n_{2 \cdot }}{n_{\cdot 1} - i} ~ \phi _2^ i ~ & = & ~ \alpha /2 \end{eqnarray*}](images/procstat_freq0416.png)
When the odds ratio equals zero, which occurs when either ![]() or
or ![]() , PROC FREQ sets the lower exact confidence limit to zero and determines the upper limit with level
, PROC FREQ sets the lower exact confidence limit to zero and determines the upper limit with level ![]() . Similarly, when the odds ratio equals infinity, which occurs when either
. Similarly, when the odds ratio equals infinity, which occurs when either ![]() or
or ![]() , PROC FREQ sets the upper exact confidence limit to infinity and determines the lower limit with level
, PROC FREQ sets the upper exact confidence limit to infinity and determines the lower limit with level ![]() .
.
These measures of relative risk are useful in cohort (prospective) study designs, where two samples are identified based on the presence or absence of an explanatory factor. The two samples are observed in future time for the binary (yes-no) response variable under study. Relative risk measures are also useful in cross-sectional studies, where two variables are observed simultaneously. See Stokes, Davis, and Koch (2012) and Agresti (2007) for more information.
The column 1 relative risk is the ratio of the column 1 risk for row 1 to row 2. The column 1 risk for row 1 is the proportion of the row 1 observations classified in column 1,
Similarly, the column 1 risk for row 2 is
The column 1 relative risk is computed as
A relative risk greater than 1 indicates that the probability of positive response is greater in row 1 than in row 2. Similarly, a relative risk less than 1 indicates that the probability of positive response is less in row 1 than in row 2. The strength of association increases with the deviation from 1.
Asymptotic ![]() % confidence limits for the column 1 relative risk are computed as
% confidence limits for the column 1 relative risk are computed as
where
and z is the ![]() percentile of the standard normal distribution. If either
percentile of the standard normal distribution. If either ![]() or
or ![]() is zero, the estimates are not computed.
is zero, the estimates are not computed.
PROC FREQ computes the column 2 relative risks in the same way.
Score confidence limits for the relative risk (Miettinen and Nurminen, 1985; Farrington and Manning, 1990) are computed by inverting score tests for the relative risk. A score-based chi-square test statistic for the null hypothesis that the relative risk equals ![]() can be expressed as
can be expressed as
where ![]() and
and ![]() are the observed row 1 and row 2 risks (proportions), respectively,
are the observed row 1 and row 2 risks (proportions), respectively,
where ![]() and
and ![]() are the maximum likelihood estimates of
are the maximum likelihood estimates of ![]() and
and ![]() , respectively, under the null hypothesis that the relative risk equals
, respectively, under the null hypothesis that the relative risk equals ![]() . For more information, see Miettinen and Nurminen (1985) and Miettinen (1985, chapter 13).
. For more information, see Miettinen and Nurminen (1985) and Miettinen (1985, chapter 13).
The ![]() % score confidence interval for the relative risk consists of all values of
% score confidence interval for the relative risk consists of all values of ![]() for which the test statistic
for which the test statistic ![]() falls in the acceptance region,
falls in the acceptance region,
where ![]() is the 100
is the 100![]() percentile of the chi-square distribution with one degree of freedom. PROC FREQ finds the confidence limits by iterative
computation. For more information about score confidence limits, see Agresti (2013).
percentile of the chi-square distribution with one degree of freedom. PROC FREQ finds the confidence limits by iterative
computation. For more information about score confidence limits, see Agresti (2013).
By default, the score confidence limits include the bias correction factor ![]() in the denominator of
in the denominator of ![]() (Miettinen and Nurminen, 1985, p. 217). If you specify the CL=SCORE(CORRECT=NO) option, PROC FREQ does not include this factor in the computation.
(Miettinen and Nurminen, 1985, p. 217). If you specify the CL=SCORE(CORRECT=NO) option, PROC FREQ does not include this factor in the computation.
The maximum likelihood estimates of ![]() and
and ![]() , subject to the constraint that the relative risk is
, subject to the constraint that the relative risk is ![]() , are computed as
, are computed as
where
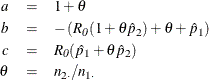
For more information, see Farrington and Manning (1990, p. 1454) and Miettinen and Nurminen (1985, p. 217).
If you specify the RELRISK option in the EXACT statement, PROC FREQ provides exact unconditional confidence limits for the
relative risk. PROC FREQ computes the confidence limits by inverting two separate one-sided tests (tail method), where the
size of each test is at most ![]() and the confidence coefficient is at least
and the confidence coefficient is at least ![]() . Exact conditional methods, described in the section Exact Statistics, do not apply to the relative risk due to the presence of a nuisance parameter (Agresti, 1992). The unconditional approach eliminates the nuisance parameter by maximizing the p-value over all possible values of the parameter (Santner and Snell, 1980).
. Exact conditional methods, described in the section Exact Statistics, do not apply to the relative risk due to the presence of a nuisance parameter (Agresti, 1992). The unconditional approach eliminates the nuisance parameter by maximizing the p-value over all possible values of the parameter (Santner and Snell, 1980).
By default, PROC FREQ uses the unstandardized relative risk as the test statistic in the confidence limit computations. If you specify the RELRISK(METHOD=SCORE) option, the procedure uses the relative risk score statistic (Chan and Zhang, 1999). The score statistic is a less discrete statistic than the raw relative risk and produces less conservative confidence limits (Agresti and Min, 2001). See also Santner et al. (2007) for comparisons of methods for computing exact confidence limits.
See the section Exact Unconditional Confidence Limits for the Risk Difference for a description of the method that PROC FREQ uses to compute confidence limits for the relative risk. The test statistic for the relative risk computation is either the unstandardized relative risk (by default) or the relative risk score statistic (if you specify the RELRISK(METHOD=SCORE) option). PROC FREQ uses the following form of the unstandardized relative risk, which adds 0.05 to each frequency, to ensure that the statistic is defined when there are zero table cells (Gart and Nam, 1988):
If you specify the RELRISK(METHOD=SCORE) option, PROC FREQ uses the relative risk score statistic (Miettinen and Nurminen, 1985; Farrington and Manning, 1990). This test statistic is computed as
where
where ![]() and
and ![]() are the maximum likelihood estimates of
are the maximum likelihood estimates of ![]() and
and ![]() under the null hypothesis that the relative risk equals
under the null hypothesis that the relative risk equals ![]() . The maximum likelihood solution is
. The maximum likelihood solution is
where
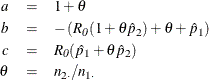
For more information, see Farrington and Manning (1990, p. 1454) and Miettinen and Nurminen (1985, p. 217).
