The HPBIN Procedure
For variable x, assume that the data set is {![]() }, where
}, where ![]() . Let
. Let ![]() , and let
, and let ![]() . The range of the variable is
. The range of the variable is ![]() .
.
The computations for the bucket, pseudo–quantile, and Winsorized binning methods are as follows:
-
For bucket binning, the length of the bucket is
![\[ L = \frac{max(x) - min(x)}{n} \]](images/prochp_hpbin0010.png)
and the split points are
![\[ s_ k = min(x) + L*k \]](images/prochp_hpbin0011.png)
where
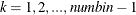 .
.
When the data are evenly distributed on the SAS appliance, the time complexity for bucket binning is
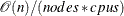 , where
, where  is the number of observations,
is the number of observations, 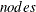 is the number of computer nodes on the appliance, and
is the number of computer nodes on the appliance, and 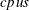 is the number of CPUs on each node.
is the number of CPUs on each node.
-
For pseudo–quantile binning and Winsorized binning, the sorting algorithm is more complex. For variable
 , a simple bucket sorting method is used to obtain the basic information. Let
, a simple bucket sorting method is used to obtain the basic information. Let 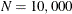 be the number of buckets, ranging from
be the number of buckets, ranging from 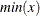 to
to 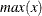 . For each bucket
. For each bucket 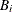 ,
, 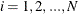 , PROC HPBIN keeps following information:
, PROC HPBIN keeps following information:
-
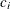 : count of
: count of  in
in 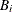
-
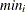 : minimum value of
: minimum value of  in
in 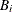
-
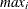 : maximum value of
: maximum value of  in
in 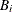
-
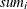 : sum of
: sum of  in
in 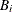
-
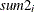 : sum of
: sum of 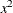 in
in 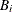
To calculate the quantile table, let
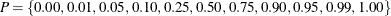 . For each
. For each 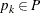 ,
, 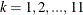 , find the smallest
, find the smallest 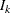 , such that
, such that 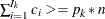 . Therefore, the quantile value
. Therefore, the quantile value 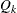 is obtained,
is obtained,
![\[ Q_ k= \begin{cases} min_{I_ k} & \text { if } \sum _{i=1}^{I_ k}{c_ i} > p_ k*n \\ max_{I_ k} & \text { if } \sum _{i=1}^{I_ k}{c_ i} = p_ k*n \end{cases} \]](images/prochp_hpbin0034.png)
where
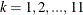 .
.
For pseudo–quantile binning, the split points are calculated. Let the base count
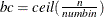 . Find those integers
. Find those integers 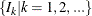 such that:
such that:
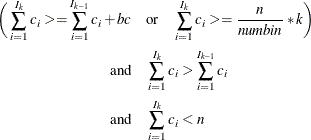
where
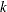 is the
is the 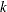 th split. The split value is
th split. The split value is
![\[ s_ k = min(x) + \frac{max(x) - min(x)}{N}*I_ k \]](images/prochp_hpbin0039.png)
where
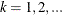 , and
, and 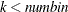 .
.
The time complexity for pseudo–quantile binning is
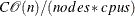 , where
, where 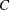 is a constant that depends on the number of sorting bucket
is a constant that depends on the number of sorting bucket 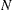 ,
,  is the number of observations,
is the number of observations, 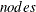 is the number of computer nodes on the appliance, and
is the number of computer nodes on the appliance, and 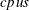 is the number of CPUs on each node.
is the number of CPUs on each node.
-
-
For Winsorized binning, the Winsorized statistics are computed first. After the minimum and maximum have been found, the split points are calculated the same way as in bucket binning.
Let the tail count
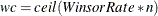 , and find the smallest
, and find the smallest 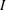 , such that
, such that 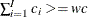 . Then, the left tail count is
. Then, the left tail count is 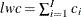 . Find the next
. Find the next 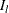 , such that
, such that 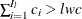 . Therefore, the minimum value is
. Therefore, the minimum value is 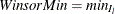 . Similarly, find the largest
. Similarly, find the largest 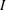 , such that
, such that 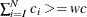 . The right tail count is
. The right tail count is 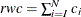 . Find the next
. Find the next 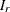 , such that
, such that 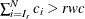 . Then the maximum value is
. Then the maximum value is 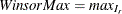 . The mean is calculated by the formula
. The mean is calculated by the formula
![\[ WinsorMean = \frac{lwc * WinsorMin + \sum _{i=I_ l}^{I_ r}{sum_ i} + rwc * WinsorMax }{n} \]](images/prochp_hpbin0056.png)
The trimmed mean is calculated by the formula
![\[ trimmedMean = \frac{\sum _{i=I_ l}^{I_ r}{sum_ i}}{n - lwc - rwc} \]](images/prochp_hpbin0057.png)
Note: If PROC HPBIN prints an error or a warning message, the results may not be accurate.
