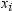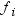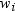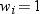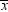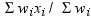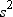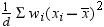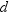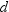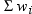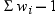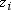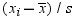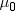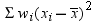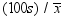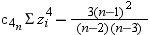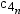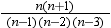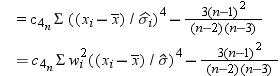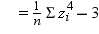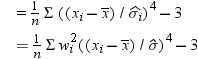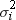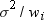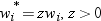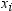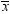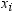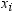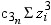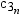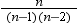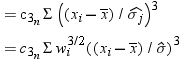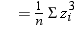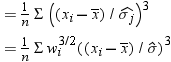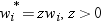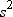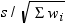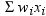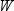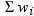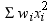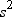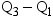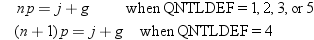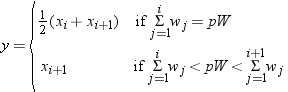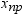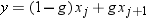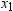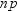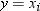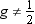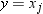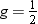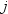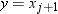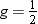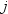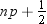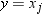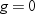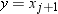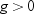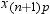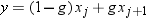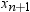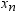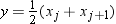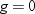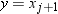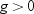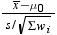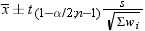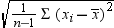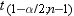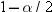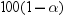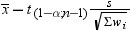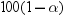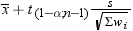Keywords and Formulas
Simple Statistics
The Base
SAS procedures use a standardized set of keywords to refer to statistics.
You specify these keywords in SAS statements to request the statistics
to be displayed or stored in an output data set.
In the following notation,
summation is over observations that contain nonmissing values of the
analyzed variable and, except where shown, over nonmissing weights
and frequencies of one or more:
is the frequency that
is associated with 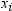 if you use a FREQ statement. If you omit the FREQ
statement, then
if you use a FREQ statement. If you omit the FREQ
statement, then 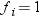 for all i.
for all i.
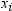 if you use a FREQ statement. If you omit the FREQ
statement, then
if you use a FREQ statement. If you omit the FREQ
statement, then 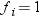 for all i.
for all i.
is the weight that
is associated with 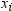 if you use a WEIGHT statement. The base procedures
automatically exclude the values of
if you use a WEIGHT statement. The base procedures
automatically exclude the values of 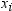 with missing weights from the analysis.
with missing weights from the analysis.
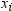 if you use a WEIGHT statement. The base procedures
automatically exclude the values of
if you use a WEIGHT statement. The base procedures
automatically exclude the values of 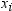 with missing weights from the analysis.
with missing weights from the analysis.
By default, the base
procedures treat a negative weight as if it is equal to zero. However,
if you use the EXCLNPWGT option in the PROC statement, then the procedure
also excludes those values of 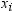 with nonpositive weights. Note that most
with nonpositive weights. Note that most SAS/STAT
procedures, such as PROC TTEST and PROC GLM, exclude values with nonpositive
weights by default.
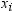 with nonpositive weights. Note that most
with nonpositive weights. Note that most is the number of nonmissing
values of 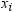 ,
, 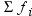 . If you use the EXCLNPWGT option and the WEIGHT
statement, then
. If you use the EXCLNPWGT option and the WEIGHT
statement, then  is the number of nonmissing values with positive
weights.
is the number of nonmissing values with positive
weights.
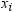 ,
, 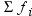 . If you use the EXCLNPWGT option and the WEIGHT
statement, then
. If you use the EXCLNPWGT option and the WEIGHT
statement, then  is the number of nonmissing values with positive
weights.
is the number of nonmissing values with positive
weights.
The standard keywords
and formulas for each statistic follow. Some formulas use keywords
to designate the corresponding statistic.
Descriptive Statistics
The keywords for descriptive
statistics are
is the number of 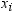 values that are not missing. Observations with
values that are not missing. Observations with
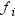 less than one and
less than one and 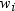 equal to missing or
equal to missing or 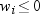 (when you use the EXCLNPWGT option) are excluded
from the analysis and are not included in the calculation of N.
(when you use the EXCLNPWGT option) are excluded
from the analysis and are not included in the calculation of N.
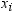 values that are not missing. Observations with
values that are not missing. Observations with
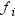 less than one and
less than one and 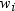 equal to missing or
equal to missing or 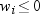 (when you use the EXCLNPWGT option) are excluded
from the analysis and are not included in the calculation of N.
(when you use the EXCLNPWGT option) are excluded
from the analysis and are not included in the calculation of N.
is the number of 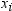 values that are missing. Observations with
values that are missing. Observations with 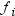 less than one and
less than one and 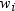 equal to missing or
equal to missing or 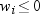 (when you use the EXCLNPWGT option) are excluded
from the analysis and are not included in the calculation of NMISS.
(when you use the EXCLNPWGT option) are excluded
from the analysis and are not included in the calculation of NMISS.
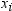 values that are missing. Observations with
values that are missing. Observations with 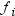 less than one and
less than one and 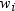 equal to missing or
equal to missing or 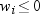 (when you use the EXCLNPWGT option) are excluded
from the analysis and are not included in the calculation of NMISS.
(when you use the EXCLNPWGT option) are excluded
from the analysis and are not included in the calculation of NMISS.
is the total number
of observations and is calculated as the sum of N and NMISS. However,
if you use the WEIGHT statement, then NOBS is calculated as the sum
of N, NMISS, and the number of observations excluded because of missing
or nonpositive weights.
Quantile and Related Statistics
The keywords for quantiles and
related statistics are
You use the QNTLDEF= option (PCTLDEF= in PROC UNIVARIATE)
to specify the method that the procedure uses to compute percentiles.
Let  be the number of nonmissing values for a variable,
and let
be the number of nonmissing values for a variable,
and let 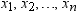 represent the ordered values of the variable such
that
represent the ordered values of the variable such
that 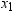 is the smallest value,
is the smallest value, 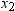 is next smallest value, and
is next smallest value, and 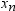 is the largest value. For the tth percentile between 0 and 1, let
is the largest value. For the tth percentile between 0 and 1, let 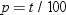 . Then define
. Then define 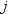 as the integer part of
as the integer part of 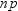 and
and 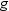 as the fractional part of
as the fractional part of 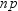 or
or 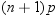 , so that
, so that
 be the number of nonmissing values for a variable,
and let
be the number of nonmissing values for a variable,
and let 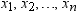 represent the ordered values of the variable such
that
represent the ordered values of the variable such
that 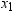 is the smallest value,
is the smallest value, 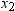 is next smallest value, and
is next smallest value, and 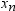 is the largest value. For the tth percentile between 0 and 1, let
is the largest value. For the tth percentile between 0 and 1, let 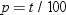 . Then define
. Then define 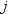 as the integer part of
as the integer part of 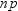 and
and 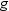 as the fractional part of
as the fractional part of 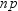 or
or 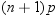 , so that
, so that
Here, QNTLDEF= specifies
the method that the procedure uses to compute the tth percentile, as shown in the table that follows.
where 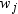 is the weight associated with
is the weight associated with 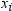 and
and 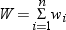 is the sum of the weights. When the observations
have identical weights, the weighted percentiles are the same as the
unweighted percentiles with QNTLDEF=5.
is the sum of the weights. When the observations
have identical weights, the weighted percentiles are the same as the
unweighted percentiles with QNTLDEF=5.
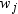 is the weight associated with
is the weight associated with 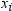 and
and 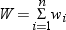 is the sum of the weights. When the observations
have identical weights, the weighted percentiles are the same as the
unweighted percentiles with QNTLDEF=5.
is the sum of the weights. When the observations
have identical weights, the weighted percentiles are the same as the
unweighted percentiles with QNTLDEF=5.
Hypothesis Testing Statistics
The keywords for hypothesis
testing statistics are
is the Student's t statistic to test the null hypothesis that
the population mean is equal to 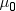 and is calculated as
and is calculated as
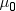 and is calculated as
and is calculated as
By default, 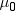 is equal to zero. You can use the MU0= option in
the PROC UNIVARIATE statement to specify
is equal to zero. You can use the MU0= option in
the PROC UNIVARIATE statement to specify 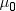 . You must use VARDEF=DF, which is the default variance
divisor, otherwise T is set to missing.
. You must use VARDEF=DF, which is the default variance
divisor, otherwise T is set to missing.
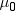 is equal to zero. You can use the MU0= option in
the PROC UNIVARIATE statement to specify
is equal to zero. You can use the MU0= option in
the PROC UNIVARIATE statement to specify 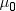 . You must use VARDEF=DF, which is the default variance
divisor, otherwise T is set to missing.
. You must use VARDEF=DF, which is the default variance
divisor, otherwise T is set to missing.
By default, when you
use a WEIGHT statement, the procedure counts the 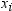 values with nonpositive weights in the degrees
of freedom. Use the EXCLNPWGT option in the PROC statement to exclude
values with nonpositive weights. Most
values with nonpositive weights in the degrees
of freedom. Use the EXCLNPWGT option in the PROC statement to exclude
values with nonpositive weights. Most SAS/STAT procedures, such as
PROC TTEST and PROC GLM automatically exclude values with nonpositive
weights.
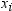 values with nonpositive weights in the degrees
of freedom. Use the EXCLNPWGT option in the PROC statement to exclude
values with nonpositive weights. Most
values with nonpositive weights in the degrees
of freedom. Use the EXCLNPWGT option in the PROC statement to exclude
values with nonpositive weights. Most