Statements
BY
Overview of the BY Statement
For more information,
see Creating Titles That Contain BY-Group Information .
Required Arguments
specifies the variable
that the procedure uses to form BY groups. You can specify more than
one variable. If you do not use the NOTSORTED option in the BY statement,
then either the observations in the data set must be sorted by all
the variables that you specify, or they must be indexed appropriately.
Variables in a BY statement are called BY variables.
Optional Arguments
specifies that the
observations are sorted in descending order by the variable that immediately
follows the word DESCENDING in the BY statement.
specifies that observations
are not necessarily sorted in alphabetic or numeric order. The observations
are grouped in another way (for example, chronological order).
The requirement for
ordering or indexing observations according to the values of BY variables
is suspended for BY-group processing when you use the
NOTSORTED option. In fact, the procedure does
not use an index if you specify NOTSORTED. The procedure defines a
BY group as a set of contiguous observations that have the same values
for all BY variables. If observations with the same values for the
BY variables are not contiguous, then the procedure treats each contiguous
set as a separate BY group.
BY-Group Processing
Procedures create output for each
BY group. For example, the elementary statistics procedures and the
scoring procedures perform separate analyses for each BY group. The
reporting procedures produce a report for each BY group.
Note: All Base SAS procedures except
PROC PRINT process BY groups independently. PROC PRINT can report
the number of observations in each BY group as well as the number
of observations in all BY groups. Similarly, PROC PRINT can sum numeric
variables in each BY group and across all BY groups.
You can use only one
BY statement in each PROC step. When you use a BY statement, the
procedure expects an input data set that is sorted by the order of
the BY variables or one that has an appropriate index. If your input
data set does not meet these criteria, then an error occurs. Either
sort it with the SORT procedure or create an appropriate index on
the BY variables.
Depending on the order
of your data, you might need to use the NOTSORTED or DESCENDING option
in the BY statement in the PROC step.
-
For more information about PROC SORT, see SORT Procedure.
-
For more information about creating indexes, see INDEX CREATE Statement.
Formatting BY-Variable Values
When a procedure is submitted with
a BY statement, the following actions are taken with respect to processing
of BY groups:
This process can have
unexpected results if, for example, nonconsecutive internal BY values
share the same formatted value. In this case, the formatted value
is represented in different BY groups. Alternatively, if different
consecutive internal BY values share the same formatted value, then
these observations are grouped into the same BY group.
BY Variables That Have Different Lengths in Two Data Sets
When a procedure has
a BY statement and two input data sets, one of the input data sets
is called the primary data set and the other is called the secondary
data set. The primary data set is usually, but not always, the DATA=
data set. A BY statement always applies to the primary data set. The
variables in the BY statement must appear in the primary data set.
Each procedure determines
whether a BY statement applies to a secondary data set, and performs
one of the following actions:
-
The procedure might check whether the BY variables are in the secondary data set. If none of the BY variables are in the secondary data set, then BY processing does not occur for the secondary data set. If one or more of the BY variables are in the secondary data set, and they match the BY variables in the primary data set, then BY processing is done for the secondary data set. If some but not all BY variables are in the secondary data set, then the procedure might issue an error message and quit. Or, it might take some other action described in the documentation for that particular procedure.
If the BY statement
is applied to the secondary data set, then each BY variable that exists
on both the data sets must have the same type, character or numeric,
in both data sets. The BY variables are required to have either the
same formatted value or the same unformatted value. Formatted values
match only if both the formatted lengths and the formatted values
are the same. Unformatted values are not required to have the same
length in order to match. The unformatted character values match if
the unformatted values are the same after stripping the trailing blanks.
The unformatted doubles match if they have the same value.
A secondary data set
does not need to have all of the BY variables that are in the primary
data set. A procedure can define a subset of the BY variables for
the secondary data set. For example, if the primary data set has the
BY variables A,B,C,D, then the procedure can define the following
BY variables on the secondary data set:
If both the primary
and secondary data sets have the same number of BY variables, and
all the BY variables have the same byte lengths and format lengths,
then either the unformatted values or the formatted values in the
BY buffer (for all of the BY variables) have to match. If they do
not match, then each variable is compared. The formatted values of
each variable are compared first. The formatted lengths have to match,
and the formatted values have to match. If the formatted lengths and
values do not match, then the unformatted values are compared even
if the byte lengths are different.
If corresponding character
variable lengths differ, then the longer character variable can contain
only trailing blanks for the extra characters. If the lengths of the
character variables are different, then the values match as long as
they are the same after stripping the trailing blanks. For example, ‘ABCD’ in the primary
data set matches ‘ABCD ’
in the secondary data set. If the secondary data set contained ‘ABCDEF’,
then they would not match.
Example
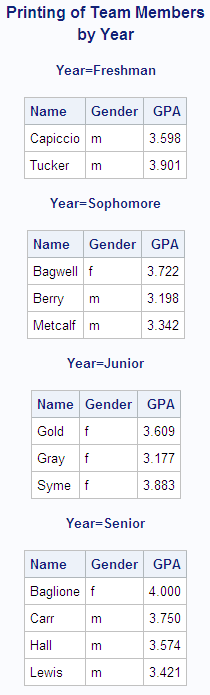
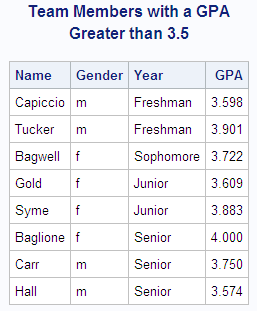
This example uses a BY statement in a PROC PRINT step.
There is output for each value of the BY variable Year. The DEBATE
data set is created in Example: Temporarily Dissociating a Format from a Variable.
FREQ
Required Arguments
specifies a numeric
variable whose value represents the frequency of the observation.
If you use the FREQ statement, then the procedure assumes that each
observation represents n observations,
where n is the value of variable.
If variable is not an integer,
then SAS truncates it. If variable is
less than 1 or is missing, then the procedure does not use that observation
to calculate statistics. If a FREQ statement does not appear, then
each observation has a default frequency of 1.
Example
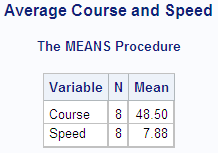
The data in this example represents a ship's course and
speed (in nautical miles per hour), recorded every hour. The frequency
variable Hours represents the number of hours that the ship maintained
the same course and speed. Each of the following PROC MEANS steps
calculates average course and speed. The different results demonstrate
the effect of using Hours as a frequency variable.
options nodate pageno=1 linesize=64 pagesize=40; data track; input Course Speed Hours @@; datalines; 30 4 8 50 7 20 75 10 30 30 8 10 80 9 22 20 8 25 83 11 6 20 6 20 ;
Without a frequency
variable, each observation has a frequency of 1, and the total number
of observations is 8.
proc means data=track maxdec=2 n mean;
var course speed;
freq hours;
title 'Average Course and Speed';
run;WEIGHT
Required Arguments
specifies a numeric
variable whose values weight the values of the analysis variables.
The values of the variable do not have to be integers. The behavior
of the procedure when it encounters a nonpositive weight variable
value is as follows:
Different behavior
for nonpositive values is discussed in the WEIGHT statement syntax
under the individual procedure.
Before Version 7 of
SAS, no Base SAS procedure excluded the observations with missing
weights from the analysis. Most SAS/STAT procedures, such as PROC
GLM, have always excluded not only missing weights but also negative
and zero weights from the analysis. You can achieve this same behavior
in a Base SAS procedure that supports the WEIGHT statement by using
the EXCLNPWGT option in the PROC statement.
The procedure substitutes
the value of the WEIGHT variable for  , which appears in Keywords and Formulas.
, which appears in Keywords and Formulas.
 , which appears in Keywords and Formulas.
, which appears in Keywords and Formulas.Calculating Weighted Statistics
The procedures that support the
WEIGHT statement also support the VARDEF= option, which lets you specify
a divisor to use in the calculation of the variance and standard deviation.
By using a WEIGHT statement
to compute moments, you assume that the ith
observation has a variance that is equal to 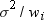 . When you specify VARDEF=DF (the default), the computed
variance is a weighted least squares estimate of
. When you specify VARDEF=DF (the default), the computed
variance is a weighted least squares estimate of 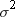 . Similarly, the computed standard deviation is an
estimate of σ. Note that the computed variance is not an estimate
of the variance of the ith
observation, because this variance involves the observation's weight,
which varies from observation to observation.
. Similarly, the computed standard deviation is an
estimate of σ. Note that the computed variance is not an estimate
of the variance of the ith
observation, because this variance involves the observation's weight,
which varies from observation to observation.
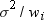 . When you specify VARDEF=DF (the default), the computed
variance is a weighted least squares estimate of
. When you specify VARDEF=DF (the default), the computed
variance is a weighted least squares estimate of 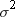 . Similarly, the computed standard deviation is an
estimate of σ. Note that the computed variance is not an estimate
of the variance of the ith
observation, because this variance involves the observation's weight,
which varies from observation to observation.
. Similarly, the computed standard deviation is an
estimate of σ. Note that the computed variance is not an estimate
of the variance of the ith
observation, because this variance involves the observation's weight,
which varies from observation to observation.
If the values of your
variable are counts that represent the number of occurrences of each
observation, then use this variable in the FREQ statement rather than
in the WEIGHT statement. In this case, because the values are counts,
they should be integers. (The FREQ statement truncates any noninteger
values.) The variance that is computed with a FREQ variable is an
estimate of the common variance 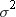 of the observations.
of the observations.
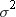 of the observations.
of the observations.
Note: If your data comes from a
stratified sample where the weights 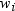 represent the strata weights, then neither the
WEIGHT statement nor the FREQ statement provides appropriate stratified
estimates of the mean, variance, or variance of the mean. To perform
the appropriate analysis, consider using PROC SURVEYMEANS, which is
a
represent the strata weights, then neither the
WEIGHT statement nor the FREQ statement provides appropriate stratified
estimates of the mean, variance, or variance of the mean. To perform
the appropriate analysis, consider using PROC SURVEYMEANS, which is
a SAS/STAT procedure that is documented in the Base SAS(R)
9.3 Procedures Guide: Statistical Procedures .
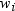 represent the strata weights, then neither the
WEIGHT statement nor the FREQ statement provides appropriate stratified
estimates of the mean, variance, or variance of the mean. To perform
the appropriate analysis, consider using PROC SURVEYMEANS, which is
a
represent the strata weights, then neither the
WEIGHT statement nor the FREQ statement provides appropriate stratified
estimates of the mean, variance, or variance of the mean. To perform
the appropriate analysis, consider using PROC SURVEYMEANS, which is
a Weighted Statistics Example
As an example of the WEIGHT statement, suppose 20 people
are asked to estimate the size of an object 30 cm wide. Each person
is placed at a different distance from the object. As the distance
from the object increases, the estimates should become less precise.
The SAS data set SIZE
contains the estimate (ObjectSize) in centimeters at each distance
(Distance) in meters and the precision (Precision) for each estimate.
Notice that the largest deviation (an overestimate by 20 cm) came
at the greatest distance (7.5 meters from the object). As a measure
of precision, 1/Distance, gives more weight to estimates that were
made closer to the object and less weight to estimates that were made
at greater distances.
options nodate pageno=1 linesize=64 pagesize=60; data size; input Distance ObjectSize @@; Precision=1/distance; datalines; 1.5 30 1.5 20 1.5 30 1.5 25 3 43 3 33 3 25 3 30 4.5 25 4.5 36 4.5 48 4.5 33 6 43 6 36 6 23 6 48 7.5 30 7.5 25 7.5 50 7.5 38 ;
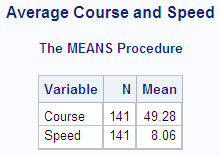
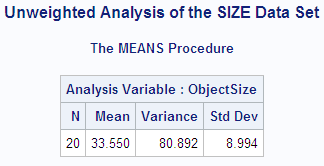
The following PROC MEANS
step computes the average estimate of the object size while ignoring
the weights. Without a WEIGHT variable, PROC MEANS uses the default
weight of 1 for every observation. Thus, the estimates of object size
at all distances are given equal weight. The average estimate of
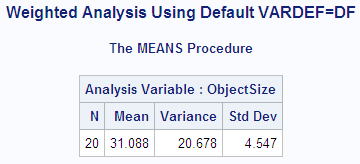
the object size exceeds the actual size by 3.55 cm.
proc means data=size maxdec=3 n mean var stddev; var objectsize; title1 'Unweighted Analysis of the SIZE Data Set'; run;
The next two PROC MEANS
steps use the precision measure (Precision) in the WEIGHT statement
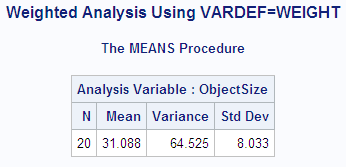
and show the effect of using different values of the VARDEF= option.
The first PROC step creates an output data set that contains the variance
and standard deviation. If you reduce the weighting of the estimates
that are made at greater distances, the weighted average estimate
of the object size is closer to the actual size.
proc means data=size maxdec=3 n mean var stddev;
weight precision;
var objectsize;
output out=wtstats var=Est_SigmaSq std=Est_Sigma;
title1 'Weighted Analysis Using Default VARDEF=DF';
run;
proc means data=size maxdec=3 n mean var std
vardef=weight;
weight precision;
var objectsize;
title1 'Weighted Analysis Using VARDEF=WEIGHT';
run;The variance of the ith
observation is assumed to be 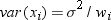 and
and 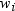 is the weight for the ith
observation. In the first PROC MEANS step, the computed variance is
an estimate of
is the weight for the ith
observation. In the first PROC MEANS step, the computed variance is
an estimate of 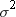 . In the second PROC MEANS step, the computed variance
is an estimate of
. In the second PROC MEANS step, the computed variance
is an estimate of 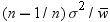 , where
, where 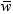 is the average weight. For large n, this value is
an approximate estimate of the variance of an observation with average
weight.
is the average weight. For large n, this value is
an approximate estimate of the variance of an observation with average
weight.
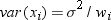 and
and 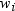 is the weight for the ith
observation. In the first PROC MEANS step, the computed variance is
an estimate of
is the weight for the ith
observation. In the first PROC MEANS step, the computed variance is
an estimate of 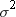 . In the second PROC MEANS step, the computed variance
is an estimate of
. In the second PROC MEANS step, the computed variance
is an estimate of 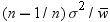 , where
, where 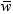 is the average weight. For large n, this value is
an approximate estimate of the variance of an observation with average
weight.
is the average weight. For large n, this value is
an approximate estimate of the variance of an observation with average
weight.
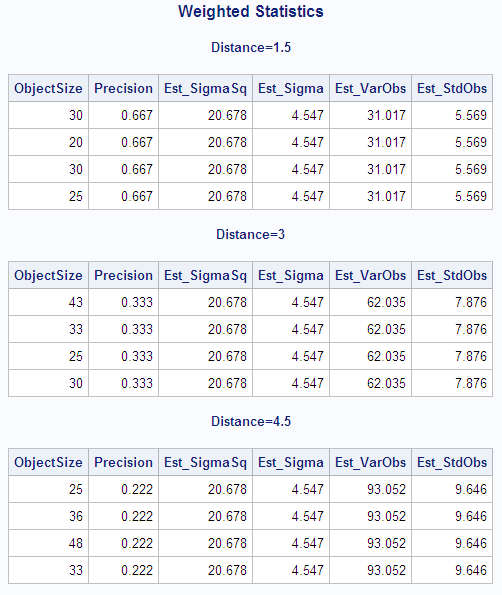
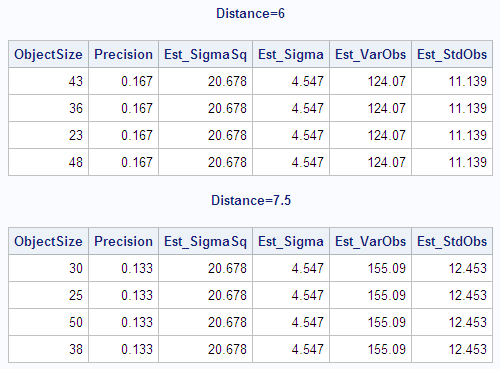
The following statements
create and print a data set with the weighted variance and weighted
standard deviation of each observation. The DATA step combines the
output data set that contains the variance and the standard deviation
from the weighted analysis with the original data set. The variance
of each observation is computed by dividing Est_SigmaSq (the estimate
of 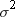 from the weighted analysis when VARDEF=DF) by each
observation's weight (Precision). The standard deviation of each observation
is computed by dividing Est_Sigma (the estimate of
from the weighted analysis when VARDEF=DF) by each
observation's weight (Precision). The standard deviation of each observation
is computed by dividing Est_Sigma (the estimate of  from the weighted analysis when VARDEF=DF) by the
square root of each observation's weight (Precision).
from the weighted analysis when VARDEF=DF) by the
square root of each observation's weight (Precision).
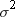 from the weighted analysis when VARDEF=DF) by each
observation's weight (Precision). The standard deviation of each observation
is computed by dividing Est_Sigma (the estimate of
from the weighted analysis when VARDEF=DF) by each
observation's weight (Precision). The standard deviation of each observation
is computed by dividing Est_Sigma (the estimate of  from the weighted analysis when VARDEF=DF) by the
square root of each observation's weight (Precision).
from the weighted analysis when VARDEF=DF) by the
square root of each observation's weight (Precision).
WHERE
Example
In this example, PROC PRINT prints only those observations
that meet the condition of the WHERE expression. The DEBATE data set
is created in Example: Temporarily Dissociating a Format from a Variable.