| Selected Examples |
Markov-modulated Poisson Arrivals
A Markov-modulated Poisson Process (MMPP) is a Poisson process
that has its parameter controlled by a Markov process.
These arrival processes are typical in communications
modeling where time-varying arrival rates capture some of the
important correlations between inter-arrival times.
This example has a Markov-modulated Poisson process that serves
to control the arrival process to a single-queue, single-server queueing
model.
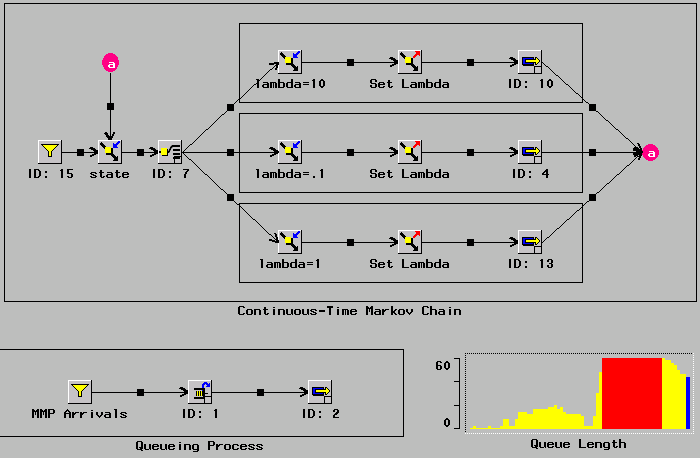
|
Figure 10.12: Markov-Modulated Poisson Arrivals
Figure 10.12 shows one way to model an MMPP.
The process labeled "Markov-modulated Poisson Process" samples
from an MMPP distribution and sets the value of the parameter
lambda, the mean inter-arrival time for an exponential random
variable in the
Sampler labeled "MMPP Arrivals."
In the upper process, lambda is given the values 10, .1, and 1,
based on the state of a Markov chain.
The state is changed in the Modifier
components labeled "state."
Each has a conditional component driven
by an observation of a uniform random variable.
So, for a given state, the state is changed to the next state and the
value of lambda is chosen for the MMPP Arrivals Sampler.
The selected lambda is set in the MMPP Arrivals Sampler,
and the process is delayed for
an exponential amount of time whose parameter is state dependent.
The transaction then goes to a switch that routes based on the
state for the next state change.
Copyright © 2008 by SAS Institute Inc., Cary, NC, USA. All rights reserved.