The DTREE Procedure

This example illustrates the use of several of the graphics options for producing graphics quality decision tree diagrams.

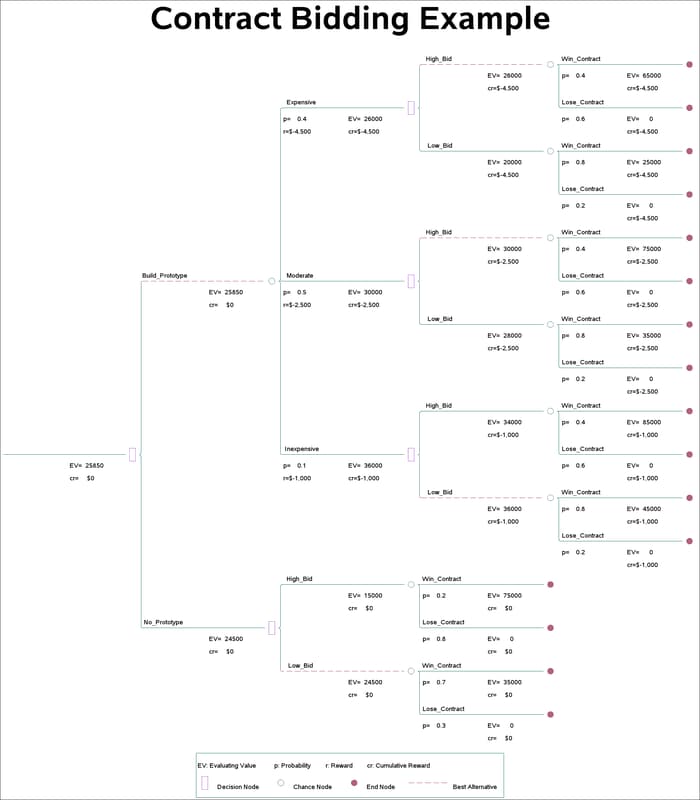
The production manager of a manufacturing company is planning to bid on a project to manufacture a new type of machine. He has the choice of bidding low or high. The evaluation of the bid will more likely be favorable if the bidder has built a prototype of the machine and includes it with the bid. However, he is uncertain about the cost of building the prototype.- His technical staff has provided him a probability distribution on the cost of the prototype.

There is also uncertainty in whether he will win the contract or not. He has estimated the probability distribution of winning the contract as shown in Table 7.21.

In addition, the payoffs of this bidding venture are affected by the cost of building the prototype. Table 7.22 shows his payoffs. The first row of the table shows the payoff is 0 if he loses the contract, regardless of whether or not he builds the prototype and whether he bids low or high. The remainder of the entries in the table give the payoff under the various scenarios.

The production manager must decide whether to build the prototype and how to bid. He uses PROC DTREE to help him to make these decisions. The structure of the model is stored in the STAGEIN= data set named Stage3. There are two decision stages, 'Choose' and 'Bid', and two chance stages, 'Cost_Prototype' and 'Contract'. The 'Choose' stage represents the decision whether or not to build a prototype. The chance stage 'Cost_Prototype' represents the uncertain cost for building a prototype. It can be 'Expensive', which costs $4,500, or 'Moderate', which costs $2,500, or 'Inexpensive', which costs $1,000. The 'Bid' stage represents the decision whether to bid high or bid low. The last stage, 'Contract', represents the result, either win the contract or lose the contract.

/* -- create the STAGEIN= data set                    -- */
data Stage3;
format _STNAME_ $14. _STTYPE_ $2. _OUTCOM_ $15.
     _SUCCES_ $14. _REWARD_ dollar8.0 ;
input _STNAME_ $16. _STTYPE_ $4. _OUTCOM_ $16.
    _SUCCES_ $16. _REWARD_ dollar8.0 ;
datalines;
Choose          D   Build_Prototype Cost_Prototype       .
.               .   No_Prototype    Bid                  .
Cost_Prototype  C   Expensive       Bid              -$4,500
.               .   Moderate        Bid              -$2,500
.               .   Inexpensive     Bid              -$1,000
Bid             D   High_Bid        Contract             .
.               .   Low_Bid         Contract             .
Contract        C   Win_Contract    .                    .
.               .   Lose_Contract   .                    .
;

The PROBIN= data set, named Prob3, contains the probability information as in Table 7.20 and Table 7.21.

/* -- create the PROBIN= data set                     -- */
data Prob3;
format _GIVEN1_ $15. _GIVEN2_ $15. _EVENT_ $14. ;
input (_GIVEN1_ _GIVEN2_ _EVENT_) ($) _PROB_;
datalines;
.               .               Expensive       0.4
.               .               Moderate        0.5
.               .               Inexpensive     0.1
Build_Prototype High_Bid        Win_Contract    0.4
Build_Prototype High_Bid        Lose_Contract   0.6
Build_Prototype Low_Bid         Win_Contract    0.8
Build_Prototype Low_Bid         Lose_Contract   0.2
No_Prototype    High_Bid        Win_Contract    0.2
No_Prototype    High_Bid        Lose_Contract   0.8
No_Prototype    Low_Bid         Win_Contract    0.7
No_Prototype    Low_Bid         Lose_Contract   0.3
;

The PAYOFFS= data set named Payoff3 contains the payoff information as in Table 7.22. Notice that the payoff to outcome 'Lose_Contract' is not in the data set Payoff3. Since PROC DTREE assigns the default value 0 to all scenarios that are not in the PAYOFFS= data set, it is not necessary to include it.

/* -- create the PAYOFFS= data set                    -- */
data Payoff3;
format _STATE1_ _STATE2_ $12.;
input (_STATE1_ _STATE2_ _ACTION_) ($16.)
    _VALUE_  dollar8.0;
datalines;
Win_Contract    .               Low_Bid         $35,000
Win_Contract    .               High_Bid        $75,000
Win_Contract    Expensive       Low_Bid         $25,000
Win_Contract    Expensive       High_Bid        $65,000
Win_Contract    Moderate        Low_Bid         $35,000
Win_Contract    Moderate        High_Bid        $75,000
Win_Contract    Inexpensive     Low_Bid         $45,000
Win_Contract    Inexpensive     High_Bid        $85,000
;

The solution, as in Output 7.3.1, is displayed on a graphics device with the following code. Notice that the title is specified before invoking PROC DTREE. The GRAPHICS option is given on the PROC DTREE statement. Specifying the COMPRESS option in the TREEPLOT statement causes the decision tree diagram to be drawn completely on one page. The vertical distance between two successive end nodes is 1 character cell (ybetween=1 cell). All text, except that in the first title line, is drawn with the font specified by the FTEXT= option.The height for all nodes is the number of character cells specified by the HSYMBOL= option. The thickness for all links in the diagram, except those that represent optimal decisions, is specified by the LWIDTH= option. The thickness of the links that represent optimal decisions is specified by the LWIDTHB= option, and the type of those links is 3 (lstyleb=3), the dash line. Colors for the text, links and nodes, and symbols to be used for nodes are not specified and hence defaults are used.

goptions ctext=black;
goptions hsize=10in htext=3.0;
 /* -- define title                                    -- */
title1 h=2 "Contract Bidding Example" ;

 /* -- PROC DTREE statements                           -- */
proc dtree stagein=Stage3 probin=Prob3 payoffs=Payoff3
     graphics
     nowarning
     ;
  evaluate;
  treeplot / name="dt3" compress ybetween=1 cell
             hsymbol=6
             lstyleb=3 lwidth=1 lwidthb=1;
quit;

With the information on this decision tree, the production manager can select the optimal bidding strategy: