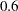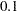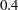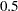The DTREE Procedure
| Oil Wildcatter’s Problem with Sounding Test |
The wildcatter is impressed with the results of calculating the values of perfect information and perfect control. After comparing those values with the costs of the sounding test and the cost-controlling procedure, he prefers to spend $ on sounding test, which has a potential improvement of $
on sounding test, which has a potential improvement of $ . He is informed that the sounding will disclose whether the terrain below has no structure (which is bad), open structure (which is okay), or closed structure (which is really hopeful). The expert also provides him with the following table, which shows the conditional probabilities.
. He is informed that the sounding will disclose whether the terrain below has no structure (which is bad), open structure (which is okay), or closed structure (which is really hopeful). The expert also provides him with the following table, which shows the conditional probabilities.
Seismic Outcomes |
|||
|---|---|---|---|
State |
No Structure |
Open Structure |
Closed Structure |
Dry |
|
|
|
Wet |
|
|
|
Soaking |
|
|
|
To include this additional information into his basic problem, the wildcatter needs to add two stages to his model: a decision stage to represent the decision whether or not to take the sounding test, and one chance stage to represent the uncertain test result. The new STAGEIN= data set is
/* -- create the STAGEIN= data set -- */
data Dtoils2;
format _STNAME_ $12. _STTYPE_ $2. _OUTCOM_ $14.
_SUCCES_ $12. _REWARD_ dollar12.0;
input _STNAME_ & _STTYPE_ & _OUTCOM_ &
_SUCCES_ & _REWARD_ dollar12.0;
datalines;
Drill D Drill Cost .
. . Not_Drill . .
Cost C Low Oil_Deposit .
. . Fair Oil_Deposit .
. . High Oil_Deposit .
Oil_Deposit C Dry . .
. . Wet . .
. . Soaking . .
Sounding D Noseismic Drill .
. . Seismic Structure -$60,000
Structure C No_Struct Drill .
. . Open_Struct Drill .
. . Closed_Struct Drill .
;
Note that the cost for the seismic soundings is represented as negative reward (of the outcome Seismic) in this data set. The conditional probabilities for stage Structure are added to the PROBIN= data set as follows:
/* -- create PROBIN= data set -- */
data Dtoilp2;
format _EVENT1 $10. _EVENT2 $12. _EVENT3 $14. ;
input _GIVEN_ $ _EVENT1 $ _PROB1
_EVENT2 $ _PROB2 _EVENT3 $ _PROB3;
datalines;
. Low 0.2 Fair 0.6 High 0.2
. Dry 0.5 Wet 0.3 Soaking 0.2
Dry No_Struct 0.6 Open_Struct 0.3 Closed_Struct 0.1
Wet No_Struct 0.3 Open_Struct 0.4 Closed_Struct 0.3
Soaking No_Struct 0.1 Open_Struct 0.4 Closed_Struct 0.5
;
It is not necessary to make any change to the PAYOFFS= data set. To evaluate his new model, the wildcatter invokes PROC DTREE as follows:
/* -- PROC DTREE statements -- */
title "Oil Wildcatter's Problem";
proc dtree stagein=Dtoils2
probin=Dtoilp2
payoffs=Dtoilu1
nowarning;
evaluate;
As before, the following messages are written to the SAS log:
NOTE: Present order of stages:
Sounding(D), Structure(C), Drill(D), Cost(C),
Oil_Deposit(C), _ENDST_(E).
NOTE: The currently optimal decision yields 140000.
The following SUMMARY statements produce optimal decision summary as shown in Figure 7.5 and Figure 7.6:
summary / target=Sounding;
summary / target=Drill;
The optimal strategy for the oil-drilling problem is found to be the following:
No soundings test should be taken, and always drill. This alternative has an expected payoff of $
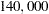 .
. If the soundings test is conducted, then drill unless the test shows the terrain below has no structure.
The soundings test is worth $
 - $
- $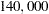 = $
= $ (this quantity is also called the value of imperfect information or the value of sample information), but it costs $
(this quantity is also called the value of imperfect information or the value of sample information), but it costs $ ; therefore, it should not be taken.
; therefore, it should not be taken.
| Oil Wildcatter's Problem |
| Order of Stages | |
|---|---|
| Stage | Type |
| Sounding | Decision |
| Structure | Chance |
| Drill | Decision |
| Cost | Chance |
| Oil_Deposit | Chance |
| _ENDST_ | End |
| Decision Parameters | |
|---|---|
| Decision Criterion: | Maximize Expected Value (MAXEV) |
| Optimal Decision Yields: | $140,000 |
| Optimal Decision Policy | ||
|---|---|---|
| Up to Stage Sounding | ||
| Alternatives or Outcomes | Cumulative Reward | Evaluating Value |
| Noseismic | $0 | $140,000* |
| Seismic | $-60,000 | $180,100 |
| Oil Wildcatter's Problem |
| Order of Stages | |
|---|---|
| Stage | Type |
| Sounding | Decision |
| Structure | Chance |
| Drill | Decision |
| Cost | Chance |
| Oil_Deposit | Chance |
| _ENDST_ | End |
| Decision Parameters | |
|---|---|
| Decision Criterion: | Maximize Expected Value (MAXEV) |
| Optimal Decision Yields: | $140,000 |
| Optimal Decision Policy | ||||
|---|---|---|---|---|
| Up to Stage Drill | ||||
| Alternatives or Outcomes | Cumulative Reward | Evaluating Value | ||
| Noseismic | Drill | $0 | $140,000* | |
| Noseismic | Not_Drill | $0 | $0 | |
| Seismic | No_Struct | Drill | $-60,000 | $-97,805 |
| Seismic | No_Struct | Not_Drill | $-60,000 | $0* |
| Seismic | Open_Struct | Drill | $-60,000 | $204,286* |
| Seismic | Open_Struct | Not_Drill | $-60,000 | $0 |
| Seismic | Closed_Struct | Drill | $-60,000 | $452,500* |
| Seismic | Closed_Struct | Not_Drill | $-60,000 | $0 |
Note that the value of sample information also can be obtained by using the following statements:
modify Seismic reward 0;
evaluate;
The following messages, which appear in the SAS log, show the expected payoff with soundings test is $ . Recall that the expected value without test information is $
. Recall that the expected value without test information is $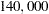 . Again, following the previous calculation, the value of test information is $
. Again, following the previous calculation, the value of test information is $ - $
- $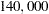 = $
= $ .
.
NOTE: The reward of outcome Seismic has been changed to 0. NOTE: The currently optimal decision yields 180100.
Now, the wildcatter has the information to make his best decision.