| The DTREE Procedure |
| Introductory Example |
A decision problem for an oil wildcatter illustrates the use of the DTREE procedure. The oil wildcatter must decide whether or not to drill at a given site before his option expires. He is uncertain about many things: the cost of drilling, the extent of the oil or gas deposits at the site, and so on. Based on the reports of his technical staff, the hole could be 'Dry' with probability 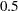 , 'Wet' with probability
, 'Wet' with probability 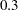 , and 'Soaking' with probability
, and 'Soaking' with probability 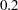 . His monetary payoffs are given in the following table.
. His monetary payoffs are given in the following table.
Drill |
Not Drill |
|
Dry |
0 |
0 |
Wet |
$ |
0 |
Soaking |
$ |
0 |
The wildcatter also learned from the reports that the cost of drilling could be $ with probability
with probability 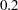 , $
, $ with probability
with probability 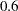 , and $
, and $ with probability
with probability 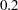 . He can gain further relevant information about the underlying geological structure of this site by conducting seismic soundings. A cost control procedure that can make the probabilities of the 'High' cost outcomes smaller (and hence, the probabilities of the 'Low' cost outcomes larger) is also available. However, such information and control are quite costly, about $
. He can gain further relevant information about the underlying geological structure of this site by conducting seismic soundings. A cost control procedure that can make the probabilities of the 'High' cost outcomes smaller (and hence, the probabilities of the 'Low' cost outcomes larger) is also available. However, such information and control are quite costly, about $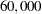 and $
and $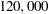 , respectively. The wildcatter must also decide whether or not to take the sounding test or the cost control program before he makes his final decision: to drill or not to drill.
, respectively. The wildcatter must also decide whether or not to take the sounding test or the cost control program before he makes his final decision: to drill or not to drill.
The oil wildcatter feels that he should structure and analyze his basic problem first: whether or not to drill. He builds a model that contains one decision stage named 'Drill' (with two outcomes, 'Drill' and 'Not_Drill') and two chance stages named 'Cost' and 'Oil_Deposit'. A representation of the model is saved in three SAS data sets. In particular, the STAGEIN= data set can be saved as follows:
/* -- create the STAGEIN= data set -- */
data Dtoils1;
format _STNAME_ $12. _STTYPE_ $2. _OUTCOM_ $10.
_SUCCES_ $12. ;
input _STNAME_ $ _STTYPE_ $ _OUTCOM_ $ _SUCCES_ $ ;
datalines;
Drill D Drill Cost
. . Not_Drill .
Cost C Low Oil_Deposit
. . Fair Oil_Deposit
. . High Oil_Deposit
Oil_Deposit C Dry .
. . Wet .
. . Soaking .
;
The structure of the decision problem is given in the Dtoils1 data set. As you apply this data set, you should be aware of the following points:
There is no reward variable in this data set; it is not necessary.
The ordering of the chance stages 'Cost' and 'Oil_Deposit' is arbitrary.
Missing values for the _SUCCES_ variable are treated as '_ENDST_' (the default name of the end stage) unless the associated outcome variable (_OUTCOM_) is also missing.
The following PROBIN= data set contains the probabilities of events:
/* -- create the PROBIN= data set -- */
data Dtoilp1;
input _EVENT1 $ _PROB1
_EVENT2 $ _PROB2
_EVENT3 $ _PROB3 ;
datalines;
Low 0.2 Fair 0.6 High 0.2
Dry 0.5 Wet 0.3 Soaking 0.2
;
Notice that the sum of the probabilities of the events 'Low', 'Fair', and 'High' is 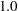 . Similarly, the sum of the probabilities of the events 'Dry', 'Wet', and 'Soaking' is
. Similarly, the sum of the probabilities of the events 'Dry', 'Wet', and 'Soaking' is 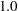 .
.
Finally, the following statements produce the PAYOFFS= data set that lists all possible scenarios and their associated payoffs.
/* -- create PAYOFFS= data set -- */ data Dtoilu1; format _STATE1-_STATE3 $12. _VALUE_ dollar12.0; input _STATE1 $ _STATE2 $ _STATE3 $ ; /* determine the cost for this scenario */ if _STATE1='Low' then _COST_=150000; else if _STATE1='Fair' then _COST_=300000; else _COST_=500000; /* determine the oil deposit and the */ /* corresponding net payoff for this scenario */ if _STATE2='Dry' then _PAYOFF_=0; else if _STATE2='Wet' then _PAYOFF_=700000; else _PAYOFF_=1200000; /* calculate the net return for this scenario */ if _STATE3='Not_Drill' then _VALUE_=0; else _VALUE_=_PAYOFF_-_COST_; /* drop unneeded variables */ drop _COST_ _PAYOFF_; datalines; Low Dry Not_Drill Low Dry Drill Low Wet Not_Drill Low Wet Drill Low Soaking Not_Drill Low Soaking Drill Fair Dry Not_Drill Fair Dry Drill Fair Wet Not_Drill Fair Wet Drill Fair Soaking Not_Drill Fair Soaking Drill High Dry Not_Drill High Dry Drill High Wet Not_Drill High Wet Drill High Soaking Not_Drill High Soaking Drill ;
This data set can be displayed, as shown in Figure 7.1, with the following PROC PRINT statements:
/* -- print the payoff table -- */ title "Oil Wildcatter's Problem"; title3 "The Payoffs"; proc print data=Dtoilu1; run;
| Oil Wildcatter's Problem |
| The Payoffs |
| Obs | _STATE1 | _STATE2 | _STATE3 | _VALUE_ |
|---|---|---|---|---|
| 1 | Low | Dry | Not_Drill | $0 |
| 2 | Low | Dry | Drill | $-150,000 |
| 3 | Low | Wet | Not_Drill | $0 |
| 4 | Low | Wet | Drill | $550,000 |
| 5 | Low | Soaking | Not_Drill | $0 |
| 6 | Low | Soaking | Drill | $1,050,000 |
| 7 | Fair | Dry | Not_Drill | $0 |
| 8 | Fair | Dry | Drill | $-300,000 |
| 9 | Fair | Wet | Not_Drill | $0 |
| 10 | Fair | Wet | Drill | $400,000 |
| 11 | Fair | Soaking | Not_Drill | $0 |
| 12 | Fair | Soaking | Drill | $900,000 |
| 13 | High | Dry | Not_Drill | $0 |
| 14 | High | Dry | Drill | $-500,000 |
| 15 | High | Wet | Not_Drill | $0 |
| 16 | High | Wet | Drill | $200,000 |
| 17 | High | Soaking | Not_Drill | $0 |
| 18 | High | Soaking | Drill | $700,000 |
The $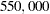 payoff associated with the scenario 'Low', 'Wet', and 'Drill' is a net figure; it represents a return of $
payoff associated with the scenario 'Low', 'Wet', and 'Drill' is a net figure; it represents a return of $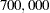 for a wet hole less the $
for a wet hole less the $ cost for drilling. Similarly, the net return of the consequence associated with the scenario 'High', 'Soaking', and 'Drill' is $
cost for drilling. Similarly, the net return of the consequence associated with the scenario 'High', 'Soaking', and 'Drill' is $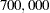 , which is interpreted as a return of $
, which is interpreted as a return of $ less the $
less the $ 'High' cost.
'High' cost.
Now the wildcatter can invoke PROC DTREE to evaluate his model and to find the optimal decision using the following statements:
/* -- PROC DTREE statements -- */
title "Oil Wildcatter's Problem";
proc dtree stagein=Dtoils1
probin=Dtoilp1
payoffs=Dtoilu1
nowarning;
evaluate / summary;
The following message, which notes the order of the stages, appears on the SAS log:
NOTE: Present order of stages:
Drill(D), Cost(C), Oil_Deposit(C), _ENDST_(E).
| Order of Stages | |
|---|---|
| Stage | Type |
| Drill | Decision |
| Cost | Chance |
| Oil_Deposit | Chance |
| _ENDST_ | End |
The SUMMARY option in the EVALUATE statement produces the optimal decision summary shown in Figure 7.2.
The summary shows that the best action, in the sense of maximizing the expected payoff, is to drill. The expected payoff for this optimal decision is $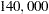 , as shown on the summary.
, as shown on the summary.
Perhaps the best way to view the details of the results is to display the complete decision tree. The following statement draws the decision tree, as shown in Figure 7.3, in line-printer format:
/* plot decision tree diagram in line-printer mode */
OPTIONS LINESIZE=100;
treeplot/ lineprinter;
Dry
-----------------------E
| p=0.5 EV= $-150,000
Low | Wet
-----------------------C-|----------------------E
| p=0.2 EV= $0 | p=0.3 EV= $550,000
| | Soaking
| -----------------------E
| p=0.2 EV= $1,050,000
| Dry
| -----------------------E
| | p=0.5 EV= $-300,000
Drill | Fair | Wet
-----------------------C-|----------------------C-|----------------------E
| EV= $0 | p=0.6 EV= $0 | p=0.3 EV= $400,000
| | | Soaking
| | -----------------------E
| | p=0.2 EV= $900,000
| | Dry
----------------------D-| | -----------------------E
EV= $0 | | | p=0.5 EV= $-500,000
| | High | Wet
| -----------------------C-|----------------------E
| p=0.2 EV= $0 | p=0.3 EV= $200,000
| | Soaking
| -----------------------E
| p=0.2 EV= $700,000
|Not_Drill
-----------------------E
EV= $0
|
Copyright © SAS Institute, Inc. All Rights Reserved.