The OPTNET Procedure
- Overview
-
Getting Started

-
Syntax
 Functional SummaryPROC OPTNET StatementBICONCOMP StatementCLIQUE StatementCONCOMP StatementCYCLE StatementDATA_ADJ_MATRIX_VAR StatementDATA_LINKS_VAR StatementDATA_MATRIX_VAR StatementDATA_NODES_VAR StatementLINEAR_ASSIGNMENT StatementMINCOSTFLOW StatementMINCUT StatementMINSPANTREE StatementSHORTPATH StatementTRANSITIVE_CLOSURE StatementTSP Statement
Functional SummaryPROC OPTNET StatementBICONCOMP StatementCLIQUE StatementCONCOMP StatementCYCLE StatementDATA_ADJ_MATRIX_VAR StatementDATA_LINKS_VAR StatementDATA_MATRIX_VAR StatementDATA_NODES_VAR StatementLINEAR_ASSIGNMENT StatementMINCOSTFLOW StatementMINCUT StatementMINSPANTREE StatementSHORTPATH StatementTRANSITIVE_CLOSURE StatementTSP Statement -
Details

-
Examples
 Articulation Points in a Terrorist NetworkCycle Detection for Kidney Donor ExchangeLinear Assignment Problem for Minimizing Swim TimesLinear Assignment Problem, Sparse Format versus Dense FormatMinimum Spanning Tree for Computer Network TopologyTransitive Closure for Identification of Circular Dependencies in a Bug Tracking SystemTraveling Salesman Tour through US Capital Cities
Articulation Points in a Terrorist NetworkCycle Detection for Kidney Donor ExchangeLinear Assignment Problem for Minimizing Swim TimesLinear Assignment Problem, Sparse Format versus Dense FormatMinimum Spanning Tree for Computer Network TopologyTransitive Closure for Identification of Circular Dependencies in a Bug Tracking SystemTraveling Salesman Tour through US Capital Cities - References
The traveling salesman problem (TSP) finds a minimum-cost tour in an undirected graph ![]() with node set
with node set ![]() and links set
and links set ![]() . A tour is a connected subgraph for which each node has degree two. The goal is then to find a tour of minimum total cost, where
the total cost is the sum of the costs of the links in the tour. With each link
. A tour is a connected subgraph for which each node has degree two. The goal is then to find a tour of minimum total cost, where
the total cost is the sum of the costs of the links in the tour. With each link ![]() , a binary variable
, a binary variable ![]() , which indicates whether link
, which indicates whether link ![]() is part of the tour, and a cost
is part of the tour, and a cost ![]() are associated. Let
are associated. Let ![]() . Then an integer linear programming formulation of the TSP is as follows:
. Then an integer linear programming formulation of the TSP is as follows:
![\[ \begin{array}{llllll} \text {minimize} & \displaystyle \sum _{(i,j) \in A} c_{ij} x_{ij} \\ \text {subject to} & \displaystyle \sum _{(i,j) \in \delta ({i})} x_{i,j} & = & 2 & i \in N & (\mr {two\_ match}) \\ & \displaystyle \sum _{(i,j) \in \delta (S)}x_{ij} & \geq & 2 & S \subset N, \; 2 \leq |S| \leq |N| - 1 & (\mr {subtour\_ elim})\\ & x_{ij} \in \{ 0,1\} & & & (i,j) \in A \end{array} \]](images/ornoaug_optnet0093.png)
The equations (two_match) are the matching constraints, which ensure that each node has degree two in the subgraph, and the inequalities (subtour_elim) are the subtour elimination constraints (SECs), which enforce connectivity.
In practical terms, you can think of the TSP in the context of a routing problem in which each node is a city and the links are roads that connect cities. Given the pairwise distances between each city, the goal is to find the shortest possible route that visits each city exactly once. The TSP has applications in planning, logistics, manufacturing, genomics, and many other areas.
In PROC OPTNET, the traveling salesman problem solver can be invoked by using the TSP statement. The options for this statement are described in the section TSP Statement.
The traveling salesman problem solver reports status information in a macro variable called _OROPTNET_TSP_. See the section Macro Variable _OROPTNET_TSP_ for more information about this macro variable.
The algorithm used in PROC OPTNET for solving TSP is based on a variant of the branch-and-cut process described in (Applegate et al., 2006).
The resulting tour is represented in two ways: In the data set that is specified in the OUT_NODES= option in the PROC OPTNET statement, the tour is given as a sequence of nodes. In the data set that is specified in the OUT= option of the TSP statement, the tour is given as a list of links in the optimal tour.
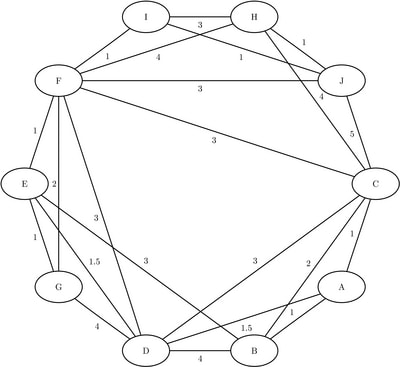
As a simple example, consider the weighted undirected graph in Figure 2.59.
The links data set can be represented as follows:
data LinkSetIn; input from $ to $ weight @@; datalines; A B 1.0 A C 1.0 A D 1.5 B C 2.0 B D 4.0 B E 3.0 C D 3.0 C F 3.0 C H 4.0 D E 1.5 D F 3.0 D G 4.0 E F 1.0 E G 1.0 F G 2.0 F H 4.0 H I 3.0 I J 1.0 C J 5.0 F J 3.0 F I 1.0 H J 1.0 ;
The following statements calculate an optimal traveling salesman tour and output the results in the data sets TSPTour and NodeSetOut:
proc optnet
loglevel = moderate
data_links = LinkSetIn
out_nodes = NodeSetOut;
tsp
out = TSPTour;
run;
%put &_OROPTNET_;
%put &_OROPTNET_TSP_;
The progress of the procedure is shown in Figure 2.60.
Figure 2.60: PROC OPTNET Log: Optimal Traveling Salesman Tour of a Simple Undirected Graph
| NOTE: ------------------------------------------------------------------------- |
| NOTE: ------------------------------------------------------------------------- |
| NOTE: Running OPTNET version 12.3. |
| NOTE: ------------------------------------------------------------------------- |
| NOTE: ------------------------------------------------------------------------- |
| NOTE: Reading the links data set. |
| NOTE: There were 22 observations read from the data set WORK.LINKSETIN. |
| NOTE: Data input used 0.01 (cpu: 0.02) seconds. |
| NOTE: Building the input graph storage used 0.00 (cpu: 0.00) seconds. |
| NOTE: The input graph storage is using 0.0 MBs of memory. |
| NOTE: The number of nodes in the input graph is 10. |
| NOTE: The number of links in the input graph is 22. |
| NOTE: ------------------------------------------------------------------------- |
| NOTE: ------------------------------------------------------------------------- |
| NOTE: Processing TSP statement. |
| NOTE: The initial TSP heuristics found a tour with cost 16 using 0.00 (cpu: |
| 0.00) seconds. |
| NOTE: The MILP presolver value NONE is applied. |
| NOTE: The MILP solver is called. |
| Node Active Sols BestInteger BestBound Gap Time |
| 0 1 2 16.0000000 16.0000000 0.00% 0 |
| 0 0 2 16.0000000 16.0000000 0.00% 0 |
| NOTE: Optimal. |
| NOTE: Objective = 16. |
| NOTE: Processing the traveling salesman problem used 0.03 (cpu: 0.00) seconds. |
| NOTE: ------------------------------------------------------------------------- |
| NOTE: ------------------------------------------------------------------------- |
| NOTE: Creating nodes data set output. |
| NOTE: Creating traveling salesman data set output. |
| NOTE: Data output used 0.00 (cpu: 0.00) seconds. |
| NOTE: ------------------------------------------------------------------------- |
| NOTE: ------------------------------------------------------------------------- |
| NOTE: The data set WORK.NODESETOUT has 10 observations and 2 variables. |
| NOTE: The data set WORK.TSPTOUR has 10 observations and 3 variables. |
| STATUS=OK TSP=OPTIMAL |
| STATUS=OPTIMAL OBJECTIVE=16 RELATIVE_GAP=0 ABSOLUTE_GAP=0 |
| PRIMAL_INFEASIBILITY=0 BOUND_INFEASIBILITY=0 INTEGER_INFEASIBILITY=0 |
| BEST_BOUND=16 NODES=1 ITERATIONS=15 CPU_TIME=0.00 REAL_TIME=0.03 |
The data set NodeSetOut now contains a sequence of nodes in the optimal tour and is shown in Figure 2.61.
Figure 2.61: Nodes in the Optimal Traveling Salesman Tour
| Traveling Salesman Problem |
| node | tsp_order |
|---|---|
| A | 1 |
| B | 2 |
| C | 3 |
| H | 4 |
| J | 5 |
| I | 6 |
| F | 7 |
| G | 8 |
| E | 9 |
| D | 10 |
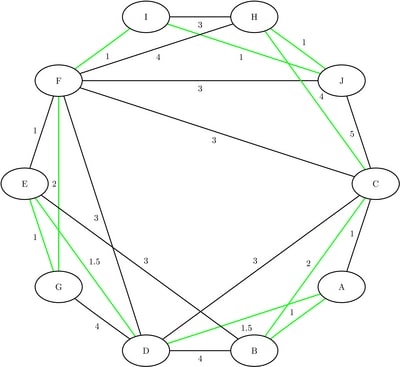
The data set TSPTour now contains the links in the optimal tour and is shown in Figure 2.62.
Figure 2.62: Links in the Optimal Traveling Salesman Tour
| Traveling Salesman Problem |
| from | to | weight |
|---|---|---|
| A | B | 1.0 |
| B | C | 2.0 |
| C | H | 4.0 |
| H | J | 1.0 |
| I | J | 1.0 |
| F | I | 1.0 |
| F | G | 2.0 |
| E | G | 1.0 |
| D | E | 1.5 |
| A | D | 1.5 |
| 16.0 |
The minimum-cost links are shown in green in Figure 2.63.