The OPTQP Procedure

Getting Started: OPTQP Procedure

Consider a small illustrative example. Suppose you want to minimize a two-variable quadratic function 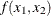$f(x_1, x_2)$ on the nonnegative quadrant, subject to two constraints:

$\begin{array}{rccccccccl} \min & 2x_1 & + & 3x_2 & + & x_1^2 & + & 10x_2^2 & + & 2.5 x_1 x_2 \\ \mbox{subject to} & x_1 & - & x_2 & \le & 1 & & & & \\ & x_1 & + & 2x_2 & \ge & 100 & & & & \\ & x_1 & & & \ge & 0 & & & & \\ & & & x_2 & \ge & 0 & & & & \end{array}$

The linear objective function coefficients, vector of right-hand sides, and lower and upper bounds are identified immediately as

$\mathbf{c} = \left[\begin{array}{c} 2 \\ 3 \end{array}\right],\quad \mathbf{b} = \left[\begin{array}{c} 1 \\ 100 \end{array}\right],\quad \mathbf{l} = \left[\begin{array}{c} 0 \\ 0 \end{array}\right],\quad \mathbf{u} = \left[\begin{array}{c} +\infty \\ +\infty \end{array}\right]$

Carefully construct the quadratic matrix 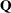$\mathbf{Q}$ . Observe that you can use symmetry to separate the main-diagonal and off-diagonal elements:

$\frac{1}{2} \mathbf{x}^\textrm {T} \mathbf{Qx} \equiv \frac{1}{2} \sum _{i, j = 1}^ n\; x_ i\, q_{ij}\, x_ j = \frac{1}{2} \sum _{i = 1}^ n\; q_{ii}\, x_ i^2 + \sum _{i > j}\; x_ i\, q_{ij}\, x_ j$

The first expression

$\frac{1}{2} \sum _{i = 1}^{n}\; q_{ii}\, x_ i^2$

sums the main-diagonal elements. Thus, in this case you have

$q_{11} = 2,\quad q_{22} = 20$

Notice that the main-diagonal values are doubled in order to accommodate the 1/2 factor. Now the second term

$\sum _{i > j} x_ i\, q_{ij}\, x_ j$

sums the off-diagonal elements in the strict lower triangular part of the matrix. The only off-diagonal (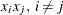 $x_ i\, x_ j,\; i\not=j$ ) term in the objective function is 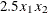$2.5\, x_1\, x_2$ , so you have

$q_{21} = 2.5$

Notice that you do not need to specify the upper triangular part of the quadratic matrix.

Finally, the matrix of constraints is as follows:

$\mathbf{A} = \left[\begin{array}{cr} 1 & -1 \\ 1 & 2 \end{array}\right]$

The SAS input data set with a quadratic programming system (QPS) format for the preceding problem can be expressed in the following manner:

data gsdata;
   input field1 $ field2 $ field3 $ field4 field5 $ field6 @;
   datalines;
NAME     .      EXAMPLE    .             .         .
ROWS     .      .          .             .         .
N        OBJ    .          .             .         .
L        R1     .          .             .         .
G        R2     .          .             .         .
COLUMNS  .      .          .             .         .
.        X1     R1         1.0           R2        1.0
.        X1     OBJ        2.0           .         .
.        X2     R1        -1.0           R2        2.0
.        X2     OBJ        3.0           .         .
RHS      .      .          .             .         .
.        RHS    R1         1.0           .         .
.        RHS    R2         100           .         .
RANGES   .      .          .             .         .
BOUNDS   .      .          .             .         .
QUADOBJ  .      .          .             .         .
.        X1     X1         2.0           .         .
.        X1     X2         2.5           .         .
.        X2     X2         20            .         .
ENDATA   .      .          .             .         .
;

For more details about the QPS-format data set, see Chapter 17: The MPS-Format SAS Data Set.

Alternatively, if you have a QPS-format flat file named gs.qps, then the following call to the SAS macro %MPS2SASD translates that file into a SAS data set, named gsdata:

%mps2sasd(mpsfile =gs.qps, outdata = gsdata);

Note: The SAS macro %MPS2SASD is provided in SAS/OR software. See Converting an MPS/QPS-Format File: %MPS2SASD for details.

You can use the following call to PROC OPTQP:

proc optqp data=gsdata
   primalout = gspout
   dualout   = gsdout;
run;

The procedure output is displayed in Figure 14.2.

Figure 14.2: Procedure Output

The OPTQP Procedure

Performance Information
Execution Mode	Single-Machine
Number of Threads	4

Problem Summary
Problem Name	EXAMPLE
Objective Sense	Minimization
Objective Function	OBJ
RHS	RHS

Number of Variables	2
Bounded Above	0
Bounded Below	2
Bounded Above and Below	0
Free	0
Fixed	0

Number of Constraints	2
LE (<=)	1
EQ (=)	0
GE (>=)	1
Range	0

Constraint Coefficients	4

Hessian Diagonal Elements	2
Hessian Elements Above the Diagonal	1

Solution Summary
Solver	QP
Algorithm	Interior Point
Objective Function	OBJ
Solution Status	Optimal
Objective Value	15018

Primal Infeasibility	0
Dual Infeasibility	0
Bound Infeasibility	0
Duality Gap	3.633377E-16
Complementarity	0

Iterations	6
Presolve Time	0.00
Solution Time	0.39

The optimal primal solution is displayed in Figure 14.3.

Figure 14.3: Optimal Solution

Obs	Objective Function ID	RHS ID	Variable Name	Variable Type	Linear Objective Coefficient	Lower Bound	Upper Bound	Variable Value	Variable Status
1	OBJ	RHS	X1	N	2	0	1.7977E308	34	O
2	OBJ	RHS	X2	N	3	0	1.7977E308	33	O

The SAS log shown in Figure 14.4 provides information about the problem, convergence information after each iteration, and the optimal objective value.

Figure 14.4: Iteration Log

NOTE: The problem EXAMPLE has 2 variables (0 free, 0 fixed).

NOTE: The problem has 2 constraints (1 LE, 0 EQ, 1 GE, 0 range).

NOTE: The problem has 4 constraint coefficients.

NOTE: The objective function has 2 Hessian diagonal elements and 1 Hessian

elements above the diagonal.

NOTE: The QP presolver value AUTOMATIC is applied.

NOTE: The QP presolver removed 0 variables and 0 constraints.

NOTE: The QP presolver removed 0 constraint coefficients.

NOTE: The presolved problem has 2 variables, 2 constraints, and 4 constraint

coefficients.

NOTE: The QP solver is called.

NOTE: The Interior Point algorithm is used.

NOTE: The deterministic parallel mode is enabled.

NOTE: The Interior Point algorithm is using up to 4 threads.

Primal Bound Dual

Iter Complement Duality Gap Infeas Infeas Infeas Time

0 3.5863E+03 4.8823E+00 1.0251E+00 1.0354E+02 2.3142E-15 0

1 1.9345E+03 9.6222E-01 4.4158E-01 4.4602E+01 5.7855E-16 0

2 2.2140E+03 1.2297E-01 4.4158E-03 4.4602E-01 5.5926E-15 0

3 5.0020E+01 3.2272E-03 4.4158E-05 4.4602E-03 9.6502E-15 0

4 4.9973E-01 3.2332E-05 4.4158E-07 4.4602E-05 2.5148E-14 0

5 4.9972E-03 3.2332E-07 4.4158E-09 4.4602E-07 3.0701E-14 0

6 0.0000E+00 3.6334E-16 1.5730E-16 0.0000E+00 1.2342E-14 0

NOTE: Optimal.

NOTE: Objective = 15018.

NOTE: The Interior Point solve time is 0.00 seconds.

NOTE: The data set WORK.GSPOUT has 2 observations and 9 variables.

NOTE: The data set WORK.GSDOUT has 2 observations and 10 variables.

See the section Interior Point Algorithm: Overview and the section Iteration Log for the OPTQP Procedure for more details about convergence information given by the iteration log.