The Nonlinear Programming Solver
A function that plays a pivotal role in establishing conditions that characterize a local minimum of an NLP problem is the
Lagrangian function ![]() , which is defined as
, which is defined as
Note that the Lagrangian function can be seen as a linear combination of the objective and constraint functions. The coefficients
of the constraints, ![]() , and
, and ![]() , are called the Lagrange multipliers or dual variables. At a feasible point
, are called the Lagrange multipliers or dual variables. At a feasible point ![]() , an inequality constraint is called active if it is satisfied as an equality—that is,
, an inequality constraint is called active if it is satisfied as an equality—that is, ![]() . The set of active constraints at a feasible point
. The set of active constraints at a feasible point ![]() is then defined as the union of the index set of the equality constraints,
is then defined as the union of the index set of the equality constraints, ![]() , and the indices of those inequality constraints that are active at
, and the indices of those inequality constraints that are active at ![]() ; that is,
; that is,
An important condition that is assumed to hold in the majority of optimization algorithms is the so-called linear independence
constraint qualification (LICQ). The LICQ states that at any feasible point ![]() , the gradients of all the active constraints are linearly independent. The main purpose of the LICQ is to ensure that the
set of constraints is well-defined in a way that there are no redundant constraints or in a way that there are no constraints
defined such that their gradients are always equal to zero.
, the gradients of all the active constraints are linearly independent. The main purpose of the LICQ is to ensure that the
set of constraints is well-defined in a way that there are no redundant constraints or in a way that there are no constraints
defined such that their gradients are always equal to zero.
If ![]() is a local minimum of the NLP problem and the LICQ holds at
is a local minimum of the NLP problem and the LICQ holds at ![]() , then there are vectors of Lagrange multipliers
, then there are vectors of Lagrange multipliers ![]() and
and ![]() , with components
, with components ![]() , and
, and ![]() , respectively, such that the following conditions are satisfied:
, respectively, such that the following conditions are satisfied:
![\[ \begin{array}{rclr} \nabla _{x} \mathcal{L}(x^{*}, y^{*}, z^{*}) & =& 0 & \\ h_{i}(x^{*}) & =& 0, & i \in \mathcal{E} \\ g_{i}(x^{*}) & \ge & 0, & i \in \mathcal{I} \\ z_{i}^{*} & \ge & 0, & i \in \mathcal{I} \\ z_{i}^{*} g_{i}(x^{*}) & =& 0, & i \in \mathcal{I} \end{array} \]](images/ormpug_nlpsolver0063.png)
where ![]() is the gradient of the Lagrangian function with respect to x, defined as
is the gradient of the Lagrangian function with respect to x, defined as
The preceding conditions are often called the Karush-Kuhn-Tucker (KKT) conditions. The last group of equations (![]() ) is called the complementarity condition. Its main aim is to try to force the Lagrange multipliers,
) is called the complementarity condition. Its main aim is to try to force the Lagrange multipliers, ![]() , of the inactive inequalities (that is, those inequalities with
, of the inactive inequalities (that is, those inequalities with ![]() ) to zero.
) to zero.
The KKT conditions describe the way the first derivatives of the objective and constraints are related at a local minimum
![]() . However, they are not enough to fully characterize a local minimum. The second-order optimality conditions attempt to fulfill
this aim by examining the curvature of the Hessian matrix of the Lagrangian function at a point that satisfies the KKT conditions.
. However, they are not enough to fully characterize a local minimum. The second-order optimality conditions attempt to fulfill
this aim by examining the curvature of the Hessian matrix of the Lagrangian function at a point that satisfies the KKT conditions.
Let ![]() be a local minimum of the NLP problem, and let
be a local minimum of the NLP problem, and let ![]() and
and ![]() be the corresponding Lagrange multipliers that satisfy the first-order optimality conditions. Then
be the corresponding Lagrange multipliers that satisfy the first-order optimality conditions. Then ![]() for all nonzero vectors d that satisfy the following conditions:
for all nonzero vectors d that satisfy the following conditions:
-
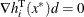 ,
, 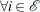
-
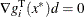 ,
, 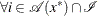 , such that
, such that 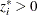
-
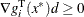 ,
, 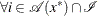 , such that
, such that 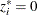
The second-order necessary optimality condition states that, at a local minimum, the curvature of the Lagrangian function along the directions that satisfy the preceding conditions must be nonnegative.
