The Decomposition Algorithm
- Overview
-
Getting Started

-
Syntax
 Decomposition Algorithm Options in the PROC OPTLP Statement or the SOLVE WITH LP Statement in PROC OPTMODELDecomposition Algorithm Options in the PROC OPTMILP Statement or the SOLVE WITH MILP Statement in PROC OPTMODELDECOMP StatementDECOMP_MASTER StatementDECOMP_MASTER_IP StatementDECOMP_SUBPROB Statement
Decomposition Algorithm Options in the PROC OPTLP Statement or the SOLVE WITH LP Statement in PROC OPTMODELDecomposition Algorithm Options in the PROC OPTMILP Statement or the SOLVE WITH MILP Statement in PROC OPTMODELDECOMP StatementDECOMP_MASTER StatementDECOMP_MASTER_IP StatementDECOMP_SUBPROB Statement -
Details

-
Examples

- References
This example describes a model for selecting tasks to be run on a shared resource (Gamrath, 2010). Consider a set ![]() of tasks and a resource capacity
of tasks and a resource capacity ![]() . Each item
. Each item ![]() has a profit
has a profit ![]() , a resource utilization level
, a resource utilization level ![]() , a starting period
, a starting period ![]() , and an ending period
, and an ending period ![]() . The time horizon considered is from the earliest starting time to the latest ending time of all tasks. With each task, associate
a binary variable
. The time horizon considered is from the earliest starting time to the latest ending time of all tasks. With each task, associate
a binary variable ![]() , which, if set to
, which, if set to ![]() , indicates that the task is running from its start time until just before its end time. A task consumes capacity if it is
running. The goal is to select which tasks to run in order to maximize profit while not exceeding the shared resource capacity.
Let
, indicates that the task is running from its start time until just before its end time. A task consumes capacity if it is
running. The goal is to select which tasks to run in order to maximize profit while not exceeding the shared resource capacity.
Let ![]() define the set of start times for all tasks, and let
define the set of start times for all tasks, and let ![]() define the set of tasks that are running at each start time
define the set of tasks that are running at each start time ![]() . The problem can be modeled as a mixed integer linear programming problem as follows:
. The problem can be modeled as a mixed integer linear programming problem as follows:
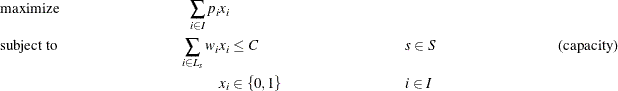
In this formulation, constraints (capacity) ensure that the running tasks do not exceed the resource capacity. To illustrate,
consider the following five-task example with data: ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . The formulation leads to a constraint matrix that has a staircase structure that is determined by tasks coming on and offline:
. The formulation leads to a constraint matrix that has a staircase structure that is determined by tasks coming on and offline:
![\[ \begin{array}{rlllllllllll} \mbox{maximize} & 6 x_1 & + & 8 x_2 & + & 5 x_3 & + & 9 x_4 & + & 8 x_5 \\ \mbox{subject to} & 8 x_1 & & & & & & & & & \leq & 10 \\ & 8 x_1 & + & 5 x_2 & & & & & & & \leq & 10 \\ & & & 5 x_2 & + & 3 x_3 & & & & & \leq & 10 \\ & & & 5 x_2 & + & 3 x_3 & + & 4 x_4 & & & \leq & 10 \\ & & & & + & 3 x_3 & + & 4 x_4 & + & 3 x_5 & \leq & 10 \\ & \multicolumn{11}{l}{x_ i \in \{ 0,1\} \quad i \in I}\\ \end{array} \]](images/ormpug_decomp0075.png)
This formulation clearly has no decomposable structure. However, you can use a common modeling technique known as Lagrangian decomposition to bring the model into block-angular form. Lagrangian decomposition works by first partitioning the constraints into blocks. Then, each original variable is split into multiple copies of itself, one copy for each block in which the variable has a nonzero coefficient in the constraint matrix. Constraints are added to enforce the equality of each copy of the original variable. Then, the original constraints can be written in block-angular form by using the duplicate variables.
To apply Lagrangian decomposition to the resource allocation problem, define a set ![]() of blocks and let
of blocks and let ![]() define the set of start times for a given block
define the set of start times for a given block ![]() , such that
, such that ![]() . Given this partition of start times, let
. Given this partition of start times, let ![]() define the set of blocks in which task
define the set of blocks in which task ![]() is scheduled to be running. Now, for each task
is scheduled to be running. Now, for each task ![]() , define duplicate variables
, define duplicate variables ![]() for each
for each ![]() . Let
. Let ![]() define the minimum block index for each class of variable that represents task
define the minimum block index for each class of variable that represents task ![]() . The problem can now be modeled in block-angular form as follows:
. The problem can now be modeled in block-angular form as follows:
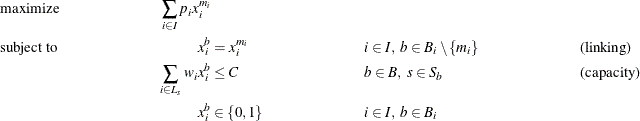
In this formulation, constraints (linking) ensure that the duplicate variables are equal to the original variables. Now, the five-task example has been transformed from a staircase structure to a block-angular structure:
![\[ \begin{array}{r*{18}{r}} \mbox{maximize} & 6 x_1^1 & + & 8 x_2^1 & + & & & 5 x_3^2 & + & 9 x_4^2 & + & & & & & 8 x_5^3 \\ \mbox{subject to} & & & x_2^1 & - & x_2^2 & & & & & & & & & & & = & 0 \\ & & & & & & & x_3^2 & - & & & x_3^3 & & & & & = & 0 \\ & & & & & & & & & x_4^2 & & & - & x_4^3 & & & = & 0 \\ & 8 x_1^1 & & & & & & & & & & & & & & & \leq & 10 \\ & 8 x_1^1 & + & 5 x_2^1 & & & & & & & & & & & & & \leq & 10 \\ & & & & & 5 x_2^2 & + & 3 x_3^2 & & & & & & & & & \leq & 10 \\ & & & & & 5 x_2^2 & + & 3 x_3^2 & + & 4 x_4^2 & & & & & & & \leq & 10 \\ & & & & & & & & & & & 3 x_3^3 & + & 4 x_4^3 & + & 3 x_5^3 & \leq & 10 \\ & \multicolumn{11}{l}{x_ i^ b \in \{ 0,1\} \quad i \in I, \ b \in B_ i}\\ \end{array} \]](images/ormpug_decomp0085.png)
To show how to apply Lagrangian decomposition in PROC OPTMODEL, consider the following data set TaskData from Caprara, Furini, and Malaguti (2010) which consists of ![]() tasks:
tasks:
data TaskData; input profit weight start end; datalines; 100 74 1 12 98 32 1 9 73 27 1 22 98 51 1 31 ... 23 40 2684 2689 36 85 2685 2687 65 44 2686 2689 18 36 2687 2689 88 57 2688 2689 ;
The following PROC OPTMODEL statements read in the data and solve the original staircase formulation by calling the MILP solver directly:
%macro SetupData(task_data=, capacity=);
set TASKS;
num capacity=&capacity;
num profit{TASKS}, weight{TASKS}, start{TASKS}, end{TASKS};
read data &task_data into TASKS=[_n_] profit weight start end;
/* the set of start times */
set STARTS = setof{i in TASKS} start[i];
/* the set of tasks i that are active at a given start time s */
set TASKS_START{s in STARTS}
= {i in TASKS: start[i] <= s < end[i]};
%mend SetupData;
%macro ResourceAllocation_Direct(task_data=, capacity=);
proc optmodel;
%SetupData(task_data=&task_data,capacity=&capacity);
/* select task i to come online from period [start to end) */
var x{TASKS} binary;
/* maximize the total profit of running tasks */
max TotalProfit = sum{i in TASKS} profit[i] * x[i];
/* enforce that the shared resource capacity is not exceeded */
con CapacityCon{s in STARTS}:
sum{i in TASKS_START[s]} weight[i] * x[i] <= capacity;
solve;
quit;
%mend ResourceAllocation_Direct;
%ResourceAllocation_Direct(task_data=TaskData, capacity=100);
The problem summary and solution summary are displayed in Output 13.5.1.
Output 13.5.1: Problem Summary and Solution Summary
| Problem Summary | |
|---|---|
| Objective Sense | Maximization |
| Objective Function | TotalProfit |
| Objective Type | Linear |
| Number of Variables | 2697 |
| Bounded Above | 0 |
| Bounded Below | 0 |
| Bounded Below and Above | 2697 |
| Free | 0 |
| Fixed | 0 |
| Binary | 2697 |
| Integer | 0 |
| Number of Constraints | 2688 |
| Linear LE (<=) | 2688 |
| Linear EQ (=) | 0 |
| Linear GE (>=) | 0 |
| Linear Range | 0 |
| Constraint Coefficients | 26880 |
| Solution Summary | |
|---|---|
| Solver | MILP |
| Algorithm | Branch and Cut |
| Objective Function | TotalProfit |
| Solution Status | Optimal within Relative Gap |
| Objective Value | 62523.999618 |
| Relative Gap | 1.5493144E-8 |
| Absolute Gap | 0.0009686933 |
| Primal Infeasibility | 0 |
| Bound Infeasibility | 1.776357E-15 |
| Integer Infeasibility | 7.3474993E-6 |
| Best Bound | 62524.000587 |
| Nodes | 441 |
| Iterations | 26866 |
| Presolve Time | 1.53 |
| Solution Time | 261.86 |
The iteration log, which contains the problem statistics, the progress of the solution, and the optimal objective value, is shown in Output 13.5.2.
Output 13.5.2: Log
| NOTE: There were 2697 observations read from the data set WORK.TASKDATA. |
| NOTE: Problem generation will use 4 threads. |
| NOTE: The problem has 2697 variables (0 free, 0 fixed). |
| NOTE: The problem has 2697 binary and 0 integer variables. |
| NOTE: The problem has 2688 linear constraints (2688 LE, 0 EQ, 0 GE, 0 range). |
| NOTE: The problem has 26880 linear constraint coefficients. |
| NOTE: The problem has 0 nonlinear constraints (0 LE, 0 EQ, 0 GE, 0 range). |
| NOTE: The OPTMODEL presolver is disabled for linear problems. |
| NOTE: The MILP presolver value AUTOMATIC is applied. |
| NOTE: The MILP presolver removed 0 variables and 0 constraints. |
| NOTE: The MILP presolver removed 0 constraint coefficients. |
| NOTE: The MILP presolver modified 0 constraint coefficients. |
| NOTE: The presolved problem has 2697 variables, 2688 constraints, and 26880 |
| constraint coefficients. |
| NOTE: The MILP solver is called. |
| Node Active Sols BestInteger BestBound Gap Time |
| 0 1 3 54182.0000000 145710 62.82% 2 |
| 0 1 3 54182.0000000 73230.2096818 26.01% 2 |
| 0 1 6 60619.0000000 70135.8936905 13.57% 3 |
| 0 1 7 61216.0000000 68409.0687245 10.51% 4 |
| 0 1 7 61216.0000000 67068.0202769 8.73% 5 |
| 0 1 7 61216.0000000 66038.0918000 7.30% 6 |
| 0 1 7 61216.0000000 65190.7829592 6.10% 7 |
| 0 1 7 61216.0000000 64529.6958613 5.14% 8 |
| 0 1 7 61216.0000000 64125.0294474 4.54% 9 |
| 0 1 7 61216.0000000 63815.0136796 4.07% 10 |
| 0 1 7 61216.0000000 63608.2185226 3.76% 10 |
| 0 1 7 61216.0000000 63404.4123225 3.45% 10 |
| 0 1 7 61216.0000000 63294.7183240 3.28% 11 |
| 0 1 7 61216.0000000 63177.6963133 3.11% 11 |
| 0 1 7 61216.0000000 63113.0842876 3.01% 11 |
| 0 1 7 61216.0000000 63066.7776464 2.93% 11 |
| 0 1 7 61216.0000000 62999.6013180 2.83% 11 |
| 0 1 7 61216.0000000 62956.5482043 2.76% 11 |
| 0 1 7 61216.0000000 62927.3931008 2.72% 11 |
| 0 1 7 61216.0000000 62910.5094398 2.69% 12 |
| 0 1 7 61216.0000000 62896.8720091 2.67% 12 |
| 0 1 7 61216.0000000 62881.4558122 2.65% 12 |
| 0 1 7 61216.0000000 62865.7212258 2.62% 12 |
| 0 1 8 61282.0000000 62865.7212258 2.52% 12 |
| 0 1 8 61282.0000000 62865.7212258 2.52% 12 |
| NOTE: The MILP solver added 1257 cuts with 8396 cut coefficients at the root. |
| 63 61 12 62424.0000000 62814.4025787 0.62% 47 |
| 100 97 12 62424.0000000 62807.4025787 0.61% 65 |
| 161 151 13 62446.0000000 62758.4665642 0.50% 99 |
| 200 187 13 62446.0000000 62739.3314203 0.47% 112 |
| 243 175 15 62465.0000000 62718.8175688 0.40% 130 |
| 251 124 17 62493.0000000 62717.7127884 0.36% 131 |
| 252 110 18 62517.0000000 62715.6822161 0.32% 131 |
| 300 102 18 62517.0000000 62603.6811810 0.14% 136 |
| 400 26 18 62517.0000000 62524.0404223 0.01% 137 |
| 440 36 19 62523.9996179 62524.0005866 0.00% 139 |
| NOTE: Optimal within relative gap. |
| NOTE: Objective = 62523.999618. |
To transform this data into block-angular form, first sort the task data to help reduce the number of duplicate variables needed in the reformulation as follows:
proc sort data=TaskData; by start end; run;
Then, create the partition of constraints into blocks of size block_size as follows:
%macro ResourceAllocation_Decomp(task_data=, capacity=, block_size=);
proc optmodel;
%SetupData(task_data=&task_data,capacity=&capacity);
/* partition into blocks of size blocks_size */
num block_size = &block_size;
num num_blocks = ceil( card(TASKS) / block_size );
set BLOCKS = 1..num_blocks;
/* the set of starts s for which task i is active */
set STARTS_TASK{i in TASKS} = {s in STARTS: start[i] <= s < end[i]};
/* partition the start times into blocks of size block_size */
set STARTS_BLOCK{BLOCKS} init {};
num block_id init 1;
num block_count init 0;
for{s in STARTS} do;
STARTS_BLOCK[block_id] = STARTS_BLOCK[block_id] union {s};
block_count = block_count + 1;
if(mod(block_count, block_size) = 0) then
block_id = block_id + 1;
end;
Then, the following PROC OPTMODEL statements define the block-angular formulation and solve the problem by using the decomposition
algorithm, the PRESOLVER=BASIC option, and block_size=40. Because this reformulation is equivalent to the original staircase formulation, disabling some of the advanced presolver
techniques ensures that the model maintains block-angularity.
/* blocks in which task i is online */
set BLOCKS_TASK{i in TASKS} =
{b in BLOCKS: card(STARTS_BLOCK[b] inter STARTS_TASK[i]) > 0};
/* minimum block id in which task i is online */
num min_block{i in TASKS} = min{b in BLOCKS_TASK[i]} b;
/* select task i to come online from period [start to end)
in each block */
var x{i in TASKS, b in BLOCKS_TASK[i]} binary;
/* maximize the total profit of running tasks */
max TotalProfit = sum{i in TASKS} profit[i] * x[i,min_block[i]];
/* enforce that task selection is consistent across blocks */
con LinkDupVarsCon{i in TASKS, b in BLOCKS_TASK[i] diff {min_block[i]}}:
x[i,b] = x[i,min_block[i]];
/* enforce that the shared resource capacity is not exceeded */
con CapacityCon{b in BLOCKS, s in STARTS_BLOCK[b]}:
sum{i in TASKS_START[s]} weight[i] * x[i,b] <= capacity;
/* define blocks for decomposition algorithm */
for{b in BLOCKS, s in STARTS_BLOCK[b]} CapacityCon[b,s].block = b;
solve with milp / presolver=basic decomp=();
quit;
%mend ResourceAllocation_Decomp;
%ResourceAllocation_Decomp(task_data=TaskData, capacity=100, block_size=40);
The problem summary and solution summary are displayed in Output 13.5.3. Compared to the original formulation, the number of variables and constraints is increased by the number of duplicate variables.
Output 13.5.3: Problem Summary and Solution Summary
| Problem Summary | |
|---|---|
| Objective Sense | Maximization |
| Objective Function | TotalProfit |
| Objective Type | Linear |
| Number of Variables | 3300 |
| Bounded Above | 0 |
| Bounded Below | 0 |
| Bounded Below and Above | 3300 |
| Free | 0 |
| Fixed | 0 |
| Binary | 3300 |
| Integer | 0 |
| Number of Constraints | 3291 |
| Linear LE (<=) | 2688 |
| Linear EQ (=) | 603 |
| Linear GE (>=) | 0 |
| Linear Range | 0 |
| Constraint Coefficients | 28086 |
| Solution Summary | |
|---|---|
| Solver | MILP |
| Algorithm | Decomposition |
| Objective Function | TotalProfit |
| Solution Status | Optimal within Relative Gap |
| Objective Value | 62524.000668 |
| Relative Gap | 0.0000640802 |
| Absolute Gap | 4.0068056181 |
| Primal Infeasibility | 6.661338E-16 |
| Bound Infeasibility | 8.881784E-16 |
| Integer Infeasibility | 8.4375E-6 |
| Best Bound | 62528.007474 |
| Nodes | 4 |
| Iterations | 55 |
| Presolve Time | 1.66 |
| Solution Time | 47.86 |
The iteration log, which contains the problem statistics, the progress of the solution, and the optimal objective value, is shown in Output 13.5.4.
Output 13.5.4: Log
| NOTE: There were 2697 observations read from the data set WORK.TASKDATA. |
| NOTE: Problem generation will use 4 threads. |
| NOTE: The problem has 3300 variables (0 free, 0 fixed). |
| NOTE: The problem has 3300 binary and 0 integer variables. |
| NOTE: The problem has 3291 linear constraints (2688 LE, 603 EQ, 0 GE, 0 range). |
| NOTE: The problem has 28086 linear constraint coefficients. |
| NOTE: The problem has 0 nonlinear constraints (0 LE, 0 EQ, 0 GE, 0 range). |
| NOTE: The MILP presolver value BASIC is applied. |
| NOTE: The MILP presolver removed 0 variables and 0 constraints. |
| NOTE: The MILP presolver removed 0 constraint coefficients. |
| NOTE: The MILP presolver modified 0 constraint coefficients. |
| NOTE: The presolved problem has 3300 variables, 3291 constraints, and 28086 |
| constraint coefficients. |
| NOTE: The MILP solver is called. |
| NOTE: The Decomposition algorithm is used. |
| NOTE: The Decomposition algorithm is executing in single-machine mode. |
| NOTE: The DECOMP method value USER is applied. |
| NOTE: The decomposition subproblems consist of 68 disjoint blocks. |
| NOTE: The decomposition subproblems cover 3300 (100.00%) variables and 2688 (81.68%) |
| constraints. |
| NOTE: The deterministic parallel mode is enabled. |
| NOTE: The Decomposition algorithm is using up to 4 threads. |
| Iter Best Master Best LP IP CPU Real |
| Bound Objective Integer Gap Gap Time Time |
| NOTE: Starting phase 1. |
| 1 0.0000 0.0000 . 0.00% . 1 0 |
| NOTE: Starting phase 2. |
| . 65890.0001 54007.0000 54007.0000 18.03% 18.03% 1 0 |
| 3 65890.0001 54659.0000 54659.0000 17.05% 17.05% 6 2 |
| 4 65890.0001 55249.0000 55249.0000 16.15% 16.15% 8 2 |
| 6 65890.0001 55639.0000 55639.0000 15.56% 15.56% 14 4 |
| 10 65890.0001 57285.3335 55639.0000 13.06% 15.56% 24 7 |
| . 65890.0001 58309.2001 57390.0000 11.51% 12.90% 24 7 |
| 16 65298.6567 61601.4676 57390.0000 5.66% 12.11% 41 12 |
| 17 64224.7955 61814.7507 57390.0000 3.75% 10.64% 44 13 |
| 18 63589.7549 62035.7507 57390.0000 2.44% 9.75% 47 14 |
| 19 63458.0056 62107.9174 57390.0000 2.13% 9.56% 49 15 |
| 20 63458.0056 62280.8344 57390.0000 1.86% 9.56% 52 16 |
| . 63458.0056 62280.8344 61498.0006 1.86% 3.09% 52 16 |
| 21 63265.1802 62280.8344 61498.0006 1.56% 2.79% 56 17 |
| 22 63003.0064 62407.2675 61498.0006 0.95% 2.39% 59 19 |
| 23 62744.1043 62418.2678 61498.0006 0.52% 1.99% 62 20 |
| 25 62682.0867 62468.8343 61498.0006 0.34% 1.89% 70 22 |
| 26 62623.1709 62491.5343 61498.0006 0.21% 1.80% 73 23 |
| 30 62623.1709 62507.0163 61498.0006 0.19% 1.80% 87 27 |
| . 62623.1709 62507.0163 61965.0006 0.19% 1.05% 87 27 |
| 31 62589.3380 62507.0163 61965.0006 0.13% 1.00% 90 28 |
| 32 62574.3405 62517.8345 61965.0006 0.09% 0.97% 93 29 |
| 33 62550.3388 62521.8345 61965.0006 0.05% 0.94% 97 30 |
| 34 62537.3384 62521.8345 61965.0006 0.02% 0.92% 99 31 |
| 35 62532.6716 62526.6679 61965.0006 0.01% 0.91% 102 32 |
| NOTE: The Decomposition algorithm stopped on the continuous RELOBJGAP= option. |
| NOTE: Starting branch and bound. |
| Node Active Sols Best Best Gap CPU Real |
| Integer Bound Time Time |
| 0 1 9 61965.0006 62532.6716 0.91% 102 32 |
| 3 1 11 62524.0007 62528.0075 0.01% 161 51 |
| NOTE: The Decomposition algorithm used 4 threads. |
| NOTE: The Decomposition algorithm time is 51.12 seconds. |
| NOTE: Optimal within relative gap. |
| NOTE: Objective = 62524.000668. |
The decomposition algorithm solves the problem in fewer nodes due to the stronger bound obtained by the reformulation. However,
it takes longer than the direct method to find a good feasible solution. The fact that the direct method seems to quickly
find good feasible solutions but has weaker bounds motivates the use of a hybrid algorithm. In the macro %ResourceAllocation_Decomp, replace the statement,
solve with milp / presolver=basic decomp=();
with the following statements:
solve with milp / relobjgap=0.1;
solve with milp / presolver=basic primalin decomp=();
These statements use the direct method with RELOBJGAP=0.1 to find a good starting solution and then use that result to seed the initial columns of the decomposition algorithm.
The solution summaries are displayed in Output 13.5.5.
Output 13.5.5: Solution Summaries
| Solution Summary | |
|---|---|
| Solver | MILP |
| Algorithm | Branch and Cut |
| Objective Function | TotalProfit |
| Solution Status | Optimal within Relative Gap |
| Objective Value | 61276 |
| Relative Gap | 0.0863603883 |
| Absolute Gap | 5792.0202769 |
| Primal Infeasibility | 0 |
| Bound Infeasibility | 0 |
| Integer Infeasibility | 0 |
| Best Bound | 67068.020277 |
| Nodes | 1 |
| Iterations | 2523 |
| Presolve Time | 1.40 |
| Solution Time | 5.07 |
| Solution Summary | |
|---|---|
| Solver | MILP |
| Algorithm | Decomposition |
| Objective Function | TotalProfit |
| Solution Status | Optimal within Relative Gap |
| Objective Value | 62524.000477 |
| Relative Gap | 0.0000559987 |
| Absolute Gap | 3.5014588178 |
| Primal Infeasibility | 1.421085E-14 |
| Bound Infeasibility | 7.327472E-15 |
| Integer Infeasibility | 8.3333333E-6 |
| Best Bound | 62527.501936 |
| Nodes | 3 |
| Iterations | 39 |
| Presolve Time | 1.63 |
| Solution Time | 35.56 |
The iteration log, which contains the problem statistics, the progress of the solution, and the optimal objective value, is shown in Output 13.5.6.
Output 13.5.6: Log
| NOTE: There were 2697 observations read from the data set WORK.TASKDATA. |
| NOTE: Problem generation will use 4 threads. |
| NOTE: The problem has 3300 variables (0 free, 0 fixed). |
| NOTE: The problem has 3300 binary and 0 integer variables. |
| NOTE: The problem has 3291 linear constraints (2688 LE, 603 EQ, 0 GE, 0 range). |
| NOTE: The problem has 28086 linear constraint coefficients. |
| NOTE: The problem has 0 nonlinear constraints (0 LE, 0 EQ, 0 GE, 0 range). |
| NOTE: The MILP presolver value AUTOMATIC is applied. |
| NOTE: The MILP presolver removed 603 variables and 603 constraints. |
| NOTE: The MILP presolver removed 1206 constraint coefficients. |
| NOTE: The MILP presolver modified 0 constraint coefficients. |
| NOTE: The presolved problem has 2697 variables, 2688 constraints, and 26880 |
| constraint coefficients. |
| NOTE: The MILP solver is called. |
| Node Active Sols BestInteger BestBound Gap Time |
| 0 1 3 54609.0000000 145710 62.52% 2 |
| 0 1 3 54609.0000000 73230.2096818 25.43% 2 |
| 0 1 6 60619.0000000 70135.8936905 13.57% 3 |
| 0 1 7 61276.0000000 68409.0687245 10.43% 4 |
| 0 1 7 61276.0000000 67068.0202769 8.64% 5 |
| NOTE: The MILP solver added 498 cuts with 2624 cut coefficients at the root. |
| NOTE: Optimal within relative gap. |
| NOTE: Objective = 61276. |
| NOTE: The MILP presolver value BASIC is applied. |
| NOTE: The MILP presolver removed 0 variables and 0 constraints. |
| NOTE: The MILP presolver removed 0 constraint coefficients. |
| NOTE: The MILP presolver modified 0 constraint coefficients. |
| NOTE: The presolved problem has 3300 variables, 3291 constraints, and 28086 |
| constraint coefficients. |
| NOTE: The MILP solver is called. |
| NOTE: The Decomposition algorithm is used. |
| NOTE: The Decomposition algorithm is executing in single-machine mode. |
| NOTE: The DECOMP method value USER is applied. |
| NOTE: The decomposition subproblems consist of 68 disjoint blocks. |
| NOTE: The decomposition subproblems cover 3300 (100.00%) variables and 2688 (81.68%) |
| constraints. |
| NOTE: The deterministic parallel mode is enabled. |
| NOTE: The Decomposition algorithm is using up to 4 threads. |
| Iter Best Master Best LP IP CPU Real |
| Bound Objective Integer Gap Gap Time Time |
| NOTE: Starting phase 1. |
| 1 0.0000 0.0000 . 0.00% . 1 0 |
| NOTE: Starting phase 2. |
| 2 65889.9999 61419.0000 61419.0000 6.79% 6.79% 3 1 |
| 3 65889.9999 61451.0000 61451.0000 6.74% 6.74% 5 1 |
| 6 65889.9999 61524.0000 61524.0000 6.63% 6.63% 12 4 |
| 10 65889.9999 61814.0000 61524.0000 6.19% 6.63% 21 7 |
| . 65889.9999 61995.0000 61561.0000 5.91% 6.57% 21 7 |
| 11 65705.2771 61995.0000 61561.0000 5.65% 6.31% 23 7 |
| 13 63865.3250 62218.3572 61561.0000 2.58% 3.61% 28 9 |
| 14 63453.5848 62378.3334 61561.0000 1.69% 2.98% 31 10 |
| 15 62892.5013 62419.1251 61561.0000 0.75% 2.12% 34 11 |
| 16 62892.5013 62487.0001 62487.0001 0.64% 0.64% 37 12 |
| 17 62892.5013 62494.0004 62494.0004 0.63% 0.63% 39 12 |
| 18 62710.3361 62521.0015 62494.0004 0.30% 0.34% 42 13 |
| 19 62636.0029 62525.0015 62494.0004 0.18% 0.23% 44 14 |
| 20 62620.3345 62527.3348 62494.0004 0.15% 0.20% 47 15 |
| . 62620.3345 62528.3338 62519.0004 0.15% 0.16% 48 15 |
| 21 62579.3348 62528.3338 62519.0004 0.08% 0.10% 51 16 |
| 22 62534.3344 62528.3338 62519.0004 0.01% 0.02% 54 17 |
| NOTE: The Decomposition algorithm stopped on the continuous RELOBJGAP= option. |
| NOTE: Starting branch and bound. |
| Node Active Sols Best Best Gap CPU Real |
| Integer Bound Time Time |
| 0 1 8 62519.0004 62534.3344 0.02% 54 17 |
| 2 0 9 62524.0005 62527.5019 0.01% 102 33 |
| NOTE: The Decomposition algorithm used 4 threads. |
| NOTE: The Decomposition algorithm time is 33.22 seconds. |
| NOTE: Optimal within relative gap. |
| NOTE: Objective = 62524.000477. |
By using this hybrid method, you can take advantage of the direct method, which finds a good feasible solution quickly, and the strong bounds provided by the decomposition algorithm. The overall time to solve the model by using the hybrid method is faster than either of the other two.
The reformulation of this resource allocation problem provides a nice example of the potential tradeoffs in modeling a problem
for use with the decomposition algorithm. As seen in Example 13.2, the strength of the bound is an important factor in the overall performance of the algorithm, but it is not always correlated
to the magnitude of the subproblem coverage. In this example, the block size determines the number of blocks. Moreover, it
determines the number of linking variables that are needed in the reformulation. At one extreme, if the block size is set
to be ![]() , then the number of blocks is 1, and the number of copies of original variables is 0. Using one block would be equivalent
to the original staircase formulation and would not yield a model conducive to decomposition. As the number of blocks is increased,
the number of linking variables increases (the size of the master problem), the strength of the decomposition bound decreases,
and the difficulty of solving the subproblems decreases. In addition, as the number of blocks and their relative difficulty
change, the efficient utilization of your machine’s parallel architecture can be affected.
, then the number of blocks is 1, and the number of copies of original variables is 0. Using one block would be equivalent
to the original staircase formulation and would not yield a model conducive to decomposition. As the number of blocks is increased,
the number of linking variables increases (the size of the master problem), the strength of the decomposition bound decreases,
and the difficulty of solving the subproblems decreases. In addition, as the number of blocks and their relative difficulty
change, the efficient utilization of your machine’s parallel architecture can be affected.
The previous section used a block size of 40. The following statement calls the decomposition algorithm and uses a block size of 130:
%ResourceAllocation_Decomp(task_data=TaskData, capacity=100, block_size=130);
The solution summary is displayed in Output 13.5.7.
Output 13.5.7: Solution Summary
| Solution Summary | |
|---|---|
| Solver | MILP |
| Algorithm | Decomposition |
| Objective Function | TotalProfit |
| Solution Status | Conditionally Optimal |
| Objective Value | 62524.000312 |
| Relative Gap | 0.0000746713 |
| Absolute Gap | 4.6690962869 |
| Primal Infeasibility | 9.5560876E-6 |
| Bound Infeasibility | 1.776357E-15 |
| Integer Infeasibility | 9.5560876E-6 |
| Best Bound | 62528.669409 |
| Nodes | 1 |
| Iterations | 22 |
| Presolve Time | 2.60 |
| Solution Time | 27.04 |
The iteration log, which contains the problem statistics, the progress of the solution, and the optimal objective value, is shown in Output 13.5.8.
Output 13.5.8: Log
| NOTE: There were 2697 observations read from the data set WORK.TASKDATA. |
| NOTE: Problem generation will use 4 threads. |
| NOTE: The problem has 2877 variables (0 free, 0 fixed). |
| NOTE: The problem has 2877 binary and 0 integer variables. |
| NOTE: The problem has 2868 linear constraints (2688 LE, 180 EQ, 0 GE, 0 range). |
| NOTE: The problem has 27240 linear constraint coefficients. |
| NOTE: The problem has 0 nonlinear constraints (0 LE, 0 EQ, 0 GE, 0 range). |
| NOTE: The MILP presolver value BASIC is applied. |
| NOTE: The MILP presolver removed 0 variables and 0 constraints. |
| NOTE: The MILP presolver removed 0 constraint coefficients. |
| NOTE: The MILP presolver modified 0 constraint coefficients. |
| NOTE: The presolved problem has 2877 variables, 2868 constraints, and 27240 |
| constraint coefficients. |
| NOTE: The MILP solver is called. |
| NOTE: The Decomposition algorithm is used. |
| NOTE: The Decomposition algorithm is executing in single-machine mode. |
| NOTE: The DECOMP method value USER is applied. |
| NOTE: The decomposition subproblems consist of 21 disjoint blocks. |
| NOTE: The decomposition subproblems cover 2877 (100.00%) variables and 2688 (93.72%) |
| constraints. |
| NOTE: The deterministic parallel mode is enabled. |
| NOTE: The Decomposition algorithm is using up to 4 threads. |
| Iter Best Master Best LP IP CPU Real |
| Bound Objective Integer Gap Gap Time Time |
| NOTE: Starting phase 1. |
| 1 0.0000 0.0000 . 0.00% . 2 0 |
| NOTE: Starting phase 2. |
| . 63337.0002 51369.0000 51369.0000 18.90% 18.90% 2 0 |
| 3 63337.0002 51989.0000 51989.0000 17.92% 17.92% 8 2 |
| 10 63337.0002 61546.0016 51989.0000 2.83% 17.92% 29 10 |
| . 63337.0002 61824.1123 60178.9998 2.39% 4.99% 29 10 |
| 13 63124.2360 62171.2306 60178.9998 1.51% 4.67% 38 13 |
| 14 63106.9999 62354.0001 60178.9998 1.19% 4.64% 40 14 |
| 15 62791.3011 62392.5003 60178.9998 0.64% 4.16% 43 15 |
| 16 62676.0007 62491.0002 60178.9998 0.30% 3.98% 46 16 |
| 17 62596.0020 62524.0003 62524.0003 0.12% 0.12% 49 17 |
| 18 62568.5024 62524.0003 62524.0003 0.07% 0.07% 52 18 |
| 19 62568.5024 62524.0003 62524.0003 0.07% 0.07% 54 19 |
| 20 62531.0027 62524.0003 62524.0003 0.01% 0.01% 57 20 |
| . 62531.0027 62524.0003 62524.0003 0.01% 0.01% 57 20 |
| 22 62528.6694 62524.0003 62524.0003 0.01% 0.01% 63 22 |
| NOTE: The Decomposition algorithm stopped on the integer RELOBJGAP= option. |
| Node Active Sols Best Best Gap CPU Real |
| Integer Bound Time Time |
| 0 0 11 62524.0003 62528.6694 0.01% 63 22 |
| NOTE: The Decomposition algorithm used 4 threads. |
| NOTE: The Decomposition algorithm time is 22.57 seconds. |
| NOTE: Conditional optimal. |
| NOTE: Objective = 62524.000312. |
This version of the model provides a stronger bound and yields better overall performance.