The Quadratic Programming Solver
Example 8.1 Linear Least Squares Problem
The linear least squares problem arises in the context of determining a solution to an overdetermined set of linear equations. In practice, these equations could arise in data fitting and estimation problems. An overdetermined system of linear equations can be defined as
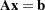 |
where 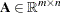 ,
, 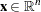 ,
, 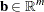 , and
, and  . Since this system usually does not have a solution, you need to be satisfied with some sort of approximate solution. The most widely used approximation is the least squares solution, which minimizes
. Since this system usually does not have a solution, you need to be satisfied with some sort of approximate solution. The most widely used approximation is the least squares solution, which minimizes  .
.
This problem is called a least squares problem for the following reason. Let 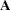 ,
,  , and
, and 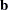 be defined as previously. Let
be defined as previously. Let 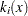 be the
be the  th component of the vector
th component of the vector 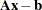 :
:
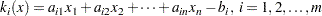 |
By definition of the Euclidean norm, the objective function can be expressed as follows:
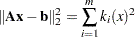 |
Therefore, the function you minimize is the sum of squares of  terms
terms 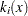 ; hence the term least squares. The following example is an illustration of the linear least squares problem; that is, each of the terms
; hence the term least squares. The following example is an illustration of the linear least squares problem; that is, each of the terms 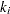 is a linear function of
is a linear function of  .
.
Consider the following least squares problem defined by
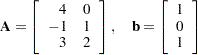 |
This translates to the following set of linear equations:
 |
The corresponding least squares problem is:
 |
The preceding objective function can be expanded to:
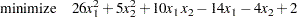 |
In addition, you impose the following constraint so that the equation 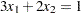 is satisfied within a tolerance of
is satisfied within a tolerance of 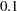 :
:
 |
You can use the following SAS statements to solve the least squares problem:
/* example 1: linear least-squares problem */
proc optmodel;
var x1; /* declare free (no explicit bounds) variable x1 */
var x2; /* declare free (no explicit bounds) variable x2 */
/* declare slack variable for ranged constraint */
var w >= 0 <= 0.2;
/* objective function: minimize is the sum of squares */
minimize f = 26 * x1 * x1 + 5 * x2 * x2 + 10 * x1 * x2
- 14 * x1 - 4 * x2 + 2;
/* subject to the following constraint */
con L: 3 * x1 + 2 * x2 - w = 0.9;
solve with qp;
/* print the optimal solution */
print x1 x2;
quit;
The output is shown in Output 8.1.1.
| Problem Summary | |
|---|---|
| Objective Sense | Minimization |
| Objective Function | f |
| Objective Type | Quadratic |
| Number of Variables | 3 |
| Bounded Above | 0 |
| Bounded Below | 0 |
| Bounded Below and Above | 1 |
| Free | 2 |
| Fixed | 0 |
| Number of Constraints | 1 |
| Linear LE (<=) | 0 |
| Linear EQ (=) | 1 |
| Linear GE (>=) | 0 |
| Linear Range | 0 |
| Constraint Coefficients | 3 |
| Solution Summary | |
|---|---|
| Solver | QP |
| Objective Function | f |
| Solution Status | Optimal |
| Objective Value | 0.0095238095 |
| Iterations | 4 |
| Primal Infeasibility | 0 |
| Dual Infeasibility | 3.940437E-17 |
| Bound Infeasibility | 0 |
| Duality Gap | 7.425058E-17 |
| Complementarity | 0 |
| x1 | x2 |
|---|---|
| 0.2381 | 0.1619 |
