Previous Page

|

Next Page

The Sequential Quadratic Programming Solver

Example 15.5 Unconstrained NLP Optimization

The SQP solver is designed mainly for constrained optimization problems, but it can also be used for solving unconstrained optimization problems. Consider the following example:

Assume the starting point 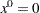. You can use the following SAS code to solve the problem:

proc optmodel;
   var x init 0;   /* starting point */
   
   minimize obj =  
      sin(x) + cos(x);
   
   solve with sqp/ printfreq = 0;
   print x;
quit;

The optimal solution is displayed in Output 15.5.1.

Output 15.5.1 Optimal Solution Using the SQP Solver

The OPTMODEL Procedure

Problem Summary
Objective Sense	Minimization
Objective Function	obj
Objective Type	Nonlinear
Number of Variables	1
Bounded Above	0
Bounded Below	0
Bounded Below and Above	0
Free	1
Fixed	0
Number of Constraints	0

Solution Summary
Solver	SQP
Objective Function	obj
Solution Status	Optimal
Objective Value	-1.414213562
Iterations	8
Infeasibility	0
Optimality Error	4.6984821E-7
Complementarity	0

x
-2.3562

You can also solve the same function by using the NLPU solver for unconstrained NLP problems. The SAS code is as follows:

proc optmodel;
   var x init 0;   /* starting point */
   
   minimize obj =  
      sin(x) + cos(x);
   
   solve;  /* the default solver is NLPU */
   print x;
quit;

The optimal solution is displayed in Output 15.5.2.

The L-BFGS method is the default technique used in the NLPU solver when a nonlinear programming problem with no variable bounds is specified. See Chapter 13, The Unconstrained Nonlinear Programming Solver, for details.

Copyright © SAS Institute, Inc. All Rights Reserved.