The Sequential Quadratic Programming Solver: Using the PENALTY= Option :: SAS/OR(R) 9.22 User's Guide: Mathematical Programming

The Sequential Quadratic Programming Solver

Example 15.4 Using the PENALTY= Option

The PENALTY= option plays an important role in ensuring a good convergence rate. Consider the following example:

$\text{[math]}$

Assume the starting point 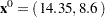$\text{[math]}$ . You can use the following SAS code to solve the problem:

proc optmodel;
   var x1 >=13 <=16, x2 >=0 <=15;
   
   minimize obj = 
      (x1-10)^3 + (x2-20)^3;
   
   con cons1:
      (x1-5)^2 + (x2-5)^2 - 100 >= 0;
   con cons2:
      82.81 - (x1-6)^2 - (x2-5)^2 >= 0;
   
   /* starting point */
   x1 = 14.35;
   x2 = 8.6;
   
   solve with sqp / printfreq = 5;
   print x1 x2;
quit;

The optimal solution is displayed in Output 15.4.1.

Output 15.4.1 Optimal Solution

The OPTMODEL Procedure

Problem Summary
Objective Sense	Minimization
Objective Function	obj
Objective Type	Nonlinear

Number of Variables	2
Bounded Above	0
Bounded Below	0
Bounded Below and Above	2
Free	0
Fixed	0

Number of Constraints	2
Linear LE (<=)	0
Linear EQ (=)	0
Linear GE (>=)	0
Linear Range	0
Nonlinear LE (<=)	0
Nonlinear EQ (=)	0
Nonlinear GE (>=)	2
Nonlinear Range	0

Solution Summary
Solver	SQP
Objective Function	obj
Solution Status	Optimal
Objective Value	-6961.815637
Iterations	46

Infeasibility	9.8124846E-7
Optimality Error	4.9473882E-7
Complementarity	9.8124846E-7

x1	x2
14.095	0.84296

The SQP solver might converge to the optimal solution more quickly if you specify PENALTY = 0.1 instead of the default value (0.75). You can specify the PENALTY= option in the SOLVE statement as follows:

   proc optmodel;
   ...
      solve with sqp / printfreq=5 penalty=0.1;
   ...
   quit;

The optimal solution is displayed in Output 15.4.2.

Output 15.4.2 Optimal Solution Using the PENALTY= Option

The OPTMODEL Procedure

Problem Summary
Objective Sense	Minimization
Objective Function	obj
Objective Type	Nonlinear

Number of Variables	2
Bounded Above	0
Bounded Below	0
Bounded Below and Above	2
Free	0
Fixed	0

Number of Constraints	2
Linear LE (<=)	0
Linear EQ (=)	0
Linear GE (>=)	0
Linear Range	0
Nonlinear LE (<=)	0
Nonlinear EQ (=)	0
Nonlinear GE (>=)	2
Nonlinear Range	0

Solution Summary
Solver	SQP
Objective Function	obj
Solution Status	Optimal
Objective Value	-6961.813512
Iterations	37

Infeasibility	0
Optimality Error	4.3943098E-6
Complementarity	2.1893472E-7

x1	x2
14.095	0.84296

The iteration log is shown in Output 15.4.3.

Output 15.4.3 Iteration Log

line

NOTE: The problem has 2 variables (0 free, 0 fixed).
NOTE: The problem has 0 linear constraints (0 LE, 0 EQ, 0 GE, 0 range).
NOTE: The problem has 2 nonlinear constraints (0 LE, 0 EQ, 2 GE, 0 range).
NOTE: The OPTMODEL presolver removed 0 variables, 0 linear constraints, and 0
nonlinear constraints.
NOTE: Using analytic derivatives for objective.
NOTE: Using analytic derivatives for nonlinear constraints.
NOTE: The SQP solver is called.
Objective Optimality
Iter Value Infeasibility Error Complementarity
0 -1399.2311250 0 0.9974417 0
5 -19631.7987648 88.0752019 0.9995422 88.0752019
10 -16744.3901937 37.9577255 0.2816822 37.9577255
15 -8732.7236696 3.3061708 0.0891951 3.3061708
20 -7951.9463937 0.8802935 0.0002608 0.8802935
25 -6825.1040194 0.3126270 0.0578253 0.9641585
30 -6998.1880026 0.0214185 0.0472124 0.8106753
35 -6962.7630171 0.0006214 0.0042324 0.0006214
37 -6961.8135125 0 0.00000439431 0.00000021893
NOTE: Converged.
NOTE: Objective = -6961.81351.

You can see from Output 15.4.2 that the SQP solver took fewer iterations to converge to the optimal solution (see Output 15.4.1).

Top of Page