| The Unconstrained Nonlinear Programming Solver |
Example 13.2 Solving the Accumulated Rosenbrock Function
Suppose you want to solve the accumulated Rosenbrock function, which contains 100 variables. For ease of understanding the formulation, define 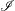 to be an ordered set of indices of the decision variables and
to be an ordered set of indices of the decision variables and 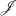 to be an ordered set of all indices in
to be an ordered set of all indices in 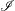 except the last one. In other words,
except the last one. In other words,
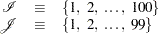 |
The mathematical formulation of the problem is as follows:
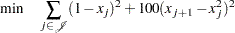 |
You can use PROC OPTMODEL to solve the problem as shown in the following statements:
proc optmodel;
set setI = {1 .. 100}; /* declare index sets */
set setJ = setI diff {100};
set elementsToPrint = {1 .. 10};
var x {setI};
minimize z = sum{j in setJ} ((1 - x[j])^2 +
100*(x[j + 1] - x[j]^2)^2);
solve with nlpu / printfreq = 0;
print {k in elementsToPrint} x[k];
quit;
The Rosenbrock function has a unique global minimizer 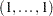 . The optimal solution is displayed in Output 13.2.1.
. The optimal solution is displayed in Output 13.2.1.
| Problem Summary | |
|---|---|
| Objective Sense | Minimization |
| Objective Function | z |
| Objective Type | Nonlinear |
| Number of Variables | 100 |
| Bounded Above | 0 |
| Bounded Below | 0 |
| Bounded Below and Above | 0 |
| Free | 100 |
| Fixed | 0 |
| Number of Constraints | 0 |
Copyright © SAS Institute, Inc. All Rights Reserved.