| The NLP Procedure |
Example 6.9 Minimize Total Delay in a Network
The following example is taken from the user’s guide of GINO (Liebman et al. 1986). A simple network of five roads (arcs) can be illustrated by the path diagram:
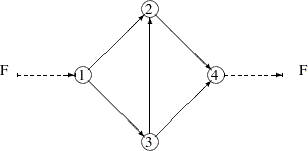
The five roads connect four intersections illustrated by numbered nodes. Each minute  vehicles enter and leave the network. Arc
vehicles enter and leave the network. Arc  refers to the road from intersection
refers to the road from intersection  to intersection
to intersection 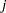 , and the parameter
, and the parameter 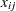 refers to the flow from
refers to the flow from 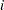 to
to 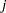 . The law that traffic flowing into each intersection
. The law that traffic flowing into each intersection 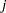 must also flow out is described by the linear equality constraint
must also flow out is described by the linear equality constraint
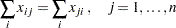 |
In general, roads also have an upper capacity, which is the number of vehicles which can be handled per minute. The upper limits 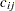 can be enforced by boundary constraints
can be enforced by boundary constraints
 |
Finding the maximum flow through a network is equivalent to solving a simple linear optimization problem, and for large problems, PROC LP or PROC NETFLOW can be used. The objective function is
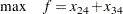 |
and the constraints are
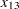 |
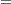 |
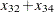 |
|||
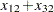 |
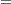 |
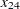 |
|||
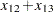 |
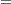 |
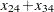 |
|||
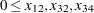 |
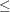 |
 |
|||
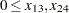 |
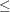 |
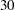 |
The three linear equality constraints are linearly dependent. One of them is deleted automatically by the PROC NLP subroutines. Even though the default technique is used for this small example, any optimization subroutine can be used.
proc nlp all initial=.5;
max y;
parms x12 x13 x32 x24 x34;
bounds x12 <= 10,
x13 <= 30,
x32 <= 10,
x24 <= 30,
x34 <= 10;
/* what flows into an intersection must flow out */
lincon x13 = x32 + x34,
x12 + x32 = x24,
x24 + x34 = x12 + x13;
y = x24 + x34 + 0*x12 + 0*x13 + 0*x32;
run;
The iteration history is given in Output 6.9.1, and the optimal solution is given in Output 6.9.2.
| Iteration | Restarts | Function Calls |
Active Constraints |
Objective Function |
Objective Function Change |
Max Abs Gradient Element |
Ridge | Ratio Between Actual and Predicted Change |
||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | * | 0 | 2 | 4 | 20.25000 | 19.2500 | 0.5774 | 0.0313 | 0.860 | |
| 2 | * | 0 | 3 | 5 | 30.00000 | 9.7500 | 0 | 0.0313 | 1.683 |
| Optimization Results | ||||
|---|---|---|---|---|
| Parameter Estimates | ||||
| N | Parameter | Estimate | Gradient Objective Function |
Active Bound Constraint |
| 1 | x12 | 10.000000 | 0 | Upper BC |
| 2 | x13 | 20.000000 | 0 | |
| 3 | x32 | 10.000000 | 0 | Upper BC |
| 4 | x24 | 20.000000 | 1.000000 | |
| 5 | x34 | 10.000000 | 1.000000 | Upper BC |
Finding a traffic pattern that minimizes the total delay to move 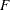 vehicles per minute from node 1 to node 4 introduces nonlinearities that, in turn, demand nonlinear optimization techniques. As traffic volume increases, speed decreases. Let
vehicles per minute from node 1 to node 4 introduces nonlinearities that, in turn, demand nonlinear optimization techniques. As traffic volume increases, speed decreases. Let 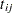 be the travel time on arc
be the travel time on arc 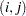 and assume that the following formulas describe the travel time as decreasing functions of the amount of traffic:
and assume that the following formulas describe the travel time as decreasing functions of the amount of traffic:
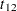 |
 |
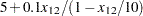 |
|||
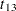 |
 |
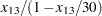 |
|||
 |
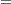 |
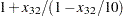 |
|||
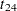 |
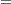 |
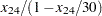 |
|||
 |
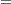 |
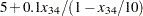 |
These formulas use the road capacities (upper bounds), assuming 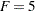 vehicles per minute have to be moved through the network. The objective function is now
vehicles per minute have to be moved through the network. The objective function is now
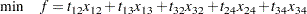 |
and the constraints are
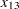 |
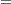 |
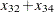 |
|||
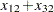 |
 |
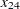 |
|||
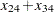 |
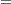 |
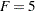 |
|||
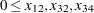 |
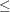 |
 |
|||
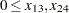 |
 |
 |
Again, the default algorithm is used:
proc nlp all initial=.5;
min y;
parms x12 x13 x32 x24 x34;
bounds x12 x13 x32 x24 x34 >= 0;
lincon x13 = x32 + x34, /* flow in = flow out */
x12 + x32 = x24,
x24 + x34 = 5; /* = f = desired flow */
t12 = 5 + .1 * x12 / (1 - x12 / 10);
t13 = x13 / (1 - x13 / 30);
t32 = 1 + x32 / (1 - x32 / 10);
t24 = x24 / (1 - x24 / 30);
t34 = 5 + .1 * x34 / (1 - x34 / 10);
y = t12*x12 + t13*x13 + t32*x32 + t24*x24 + t34*x34;
run;
The iteration history is given in Output 6.9.3, and the optimal solution is given in Output 6.9.4.
| Iteration | Restarts | Function Calls |
Active Constraints |
Objective Function |
Objective Function Change |
Max Abs Gradient Element |
Ridge | Ratio Between Actual and Predicted Change |
||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 2 | 4 | 40.30303 | 0.3433 | 4.44E-16 | 0 | 0.508 |
| Optimization Results | |||
|---|---|---|---|
| Iterations | 1 | Function Calls | 3 |
| Hessian Calls | 2 | Active Constraints | 4 |
| Objective Function | 40.303030303 | Max Abs Gradient Element | 4.440892E-16 |
| Ridge | 0 | Actual Over Pred Change | 0.5083585587 |
| Optimization Results | ||||
|---|---|---|---|---|
| Parameter Estimates | ||||
| N | Parameter | Estimate | Gradient Objective Function |
Active Bound Constraint |
| 1 | x12 | 2.500000 | 5.777778 | |
| 2 | x13 | 2.500000 | 5.702479 | |
| 3 | x32 | -2.77556E-17 | 1.000000 | Lower BC |
| 4 | x24 | 2.500000 | 5.702479 | |
| 5 | x34 | 2.500000 | 5.777778 | |
The active constraints and corresponding Lagrange multiplier estimates (costs) are given in Output 6.9.5 and Output 6.9.6, respectively.
| Linear Constraints Evaluated at Solution | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | ACT | 0 | = | 0 | + | 1.0000 | * | x13 | - | 1.0000 | * | x32 | - | 1.0000 | * | x34 |
| 2 | ACT | 4.4409E-16 | = | 0 | + | 1.0000 | * | x12 | + | 1.0000 | * | x32 | - | 1.0000 | * | x24 |
| 3 | ACT | 0 | = | -5.0000 | + | 1.0000 | * | x24 | + | 1.0000 | * | x34 | ||||
| First Order Lagrange Multipliers | ||
|---|---|---|
| Active Constraint | Lagrange Multiplier |
|
| Lower BC | x32 | 0.924702 |
| Linear EC | [1] | 5.702479 |
| Linear EC | [2] | 5.777778 |
| Linear EC | [3] | 11.480257 |
Output 6.9.7 shows that the projected gradient is very small, satisfying the first-order optimality criterion.
| Projected Gradient | |
|---|---|
| Free Dimension |
Projected Gradient |
| 1 | 4.440892E-16 |
The projected Hessian matrix (shown in Output 6.9.8) is positive definite, satisfying the second-order optimality criterion.
| Projected Hessian Matrix | |
|---|---|
| X1 | |
| X1 | 1.535309013 |
Copyright © SAS Institute, Inc. All Rights Reserved.