Previous Page | Next Page

The NLP Procedure

Example 6.6 Maximum Likelihood Weibull Estimation

Two-Parameter Weibull Estimation

The following data are taken from Lawless (1982, p. 193) and represent the number of days it took rats painted with a carcinogen to develop carcinoma. The last two observations are censored data from a group of 19 rats: 

data pike;
   input days cens @@;
   datalines;
143  0  164  0  188  0  188  0
190  0  192  0  206  0  209  0
213  0  216  0  220  0  227  0
230  0  234  0  246  0  265  0
304  0  216  1  244  1
;

Suppose that you want to show how to compute the maximum likelihood estimates of the scale parameter ( in Lawless), the shape parameter ( 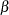in Lawless), and the location parameter 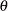( 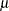in Lawless). The observed likelihood function of the three-parameter Weibull transformation (Lawless 1982, p. 191) is

     

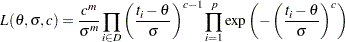and the log likelihood is

     

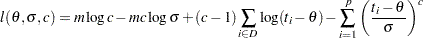The log likelihood function can be evaluated only for 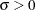, , 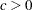and . In the estimation process, you must enforce these conditions using lower and upper boundary constraints. The three-parameter Weibull estimation can be numerically difficult, and it usually pays off to provide good initial estimates. Therefore, you first estimate and of the two-parameter Weibull distribution for constant 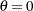. You then use the optimal parameters 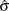and 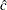as starting values for the three-parameter Weibull estimation.

Although the use of an INEST= data set is not really necessary for this simple example, it illustrates how it is used to specify starting values and lower boundary constraints: 

data par1(type=est);
   keep _type_ sig c theta;
   _type_='parms'; sig = .5;
      c = .5; theta = 0; output;
   _type_='lb'; sig = 1.0e-6;
      c = 1.0e-6; theta = .;  output;
run;

The following PROC NLP call specifies the maximization of the log likelihood function for the two-parameter Weibull estimation for constant :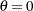 

proc nlp data=pike tech=tr inest=par1 outest=opar1
     outmodel=model cov=2 vardef=n pcov phes;
           max logf;
   parms sig c;
   profile sig c / alpha = .9 to .1 by -.1 .09 to .01 by -.01;

   x_th = days - theta;
   s    = - (x_th / sig)**c;
   if cens=0 then s + log(c) - c*log(sig) + (c-1)*log(x_th);
   logf = s;
run;

After a few iterations you obtain the solution given in Output 6.6.1.

Output 6.6.1 Optimization Results
PROC NLP: Nonlinear Maximization

Optimization Results
Parameter Estimates
N Parameter Estimate Approx
Std Err		 t Value Approx
Pr > |t|		 Gradient
Objective
Function
1 sig 234.318611 9.645908 24.292021 9.050475E-16 1.3372183E-9
2 c 6.083147 1.068229 5.694611 0.000017269 -7.859277E-9


Value of Objective Function = -88.23273515

Since the gradient has only small elements and the Hessian (shown in Output 6.6.2) is negative definite (has only negative eigenvalues), the solution defines an isolated maximum point.

Output 6.6.2 Hessian Matrix at
PROC NLP: Nonlinear Maximization

Hessian Matrix
  sig c
sig -0.011457556 0.0257527577
c 0.0257527577 -0.934221388


Determinant = 0.0100406894


Matrix has Only Negative Eigenvalues

The square roots of the diagonal elements of the approximate covariance matrix of parameter estimates are the approximate standard errors (ASE’s). The covariance matrix is given in Output 6.6.3.

Output 6.6.3 Covariance Matrix
PROC NLP: Nonlinear Maximization

Covariance Matrix 2: H = (NOBS/d)
inv(G)
  sig c
sig 93.043549863 2.5648395794
c 2.5648395794 1.141112488


Factor sigm = 1


Determinant = 99.594754608


Matrix has 2 Positive Eigenvalue(s)

The confidence limits in Output 6.6.4 correspond to the values in the PROFILE statement.

Output 6.6.4 Confidence Limits
PROC NLP: Nonlinear Maximization

Wald and PL Confidence Limits
N Parameter Estimate Alpha Profile Likelihood Confidence
Limits		 Wald Confidence Limits
1 sig 234.318611 0.900000 233.111324 235.532695 233.106494 235.530729
1 sig . 0.800000 231.886549 236.772876 231.874849 236.762374
1 sig . 0.700000 230.623280 238.063824 230.601846 238.035377
1 sig . 0.600000 229.292797 239.436639 229.260292 239.376931
1 sig . 0.500000 227.855829 240.935290 227.812545 240.824678
1 sig . 0.400000 226.251597 242.629201 226.200410 242.436813
1 sig . 0.300000 224.372260 244.643392 224.321270 244.315953
1 sig . 0.200000 221.984557 247.278423 221.956882 246.680341
1 sig . 0.100000 218.390824 251.394102 218.452504 250.184719
1 sig . 0.090000 217.884162 251.987489 217.964960 250.672263
1 sig . 0.080000 217.326988 252.645278 217.431654 251.205569
1 sig . 0.070000 216.708814 253.383546 216.841087 251.796136
1 sig . 0.060000 216.008815 254.228034 216.176649 252.460574
1 sig . 0.050000 215.199301 255.215496 215.412978 253.224245
1 sig . 0.040000 214.230116 256.411041 214.508337 254.128885
1 sig . 0.030000 213.020874 257.935686 213.386118 255.251105
1 sig . 0.020000 211.369067 260.066128 211.878873 256.758350
1 sig . 0.010000 208.671091 263.687174 209.472398 259.164825
2 c 6.083147 0.900000 5.950029 6.217752 5.948912 6.217382
2 c . 0.800000 5.815559 6.355576 5.812514 6.353780
2 c . 0.700000 5.677909 6.499187 5.671537 6.494757
2 c . 0.600000 5.534275 6.651789 5.522967 6.643327
2 c . 0.500000 5.380952 6.817880 5.362638 6.803656
2 c . 0.400000 5.212344 7.004485 5.184103 6.982191
2 c . 0.300000 5.018784 7.225733 4.975999 7.190295
2 c . 0.200000 4.776379 7.506166 4.714157 7.452137
2 c . 0.100000 4.431310 7.931669 4.326067 7.840227
2 c . 0.090000 4.382687 7.991457 4.272075 7.894220
2 c . 0.080000 4.327815 8.056628 4.213014 7.953280
2 c . 0.070000 4.270773 8.129238 4.147612 8.018682
2 c . 0.060000 4.207130 8.211221 4.074029 8.092265
2 c . 0.050000 4.134675 8.306218 3.989457 8.176837
2 c . 0.040000 4.049531 8.418782 3.889274 8.277021
2 c . 0.030000 3.945037 8.559677 3.764994 8.401300
2 c . 0.020000 3.805759 8.749130 3.598076 8.568219
2 c . 0.010000 3.588814 9.056751 3.331572 8.834722

Three-Parameter Weibull Estimation

You now prepare for the three-parameter Weibull estimation by using PROC UNIVARIATE to obtain the smallest data value for the upper boundary constraint for 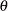. For this small problem, you can do this much more simply by just using a value slightly smaller than the minimum data value 143. 

/* Calculate upper bound for theta parameter */
proc univariate data=pike noprint;
   var days;
   output out=stats n=nobs min=minx range=range;
run;

data stats;
   set stats;
   keep _type_ theta;

   /* 1. write parms observation */
   theta = minx - .1 * range;
   if theta < 0 then theta = 0;
   _type_ = 'parms'; 
   output;

   /* 2. write ub observation */
   theta = minx * (1 - 1e-4);
   _type_ = 'ub'; 
   output;
run;

The data set PAR2 specifies the starting values and the lower and upper bounds for the three-parameter Weibull problem: 

proc sort data=opar1;
   by _type_;
run;

data par2(type=est);
   merge opar1(drop=theta) stats;
   by _type_;
   keep _type_ sig c theta;
   if _type_ in ('parms' 'lowerbd' 'ub');
run;

The following PROC NLP call uses the MODEL= input data set containing the log likelihood function that was saved during the two-parameter Weibull estimation: 

proc nlp data=pike tech=tr inest=par2 outest=opar2
      model=model cov=2 vardef=n pcov phes;
   max logf;
   parms sig c theta;
   profile sig c theta / alpha = .5 .1 .05 .01;
run;

After a few iterations, you obtain the solution given in Output 6.6.5.

Output 6.6.5 Optimization Results
PROC NLP: Nonlinear Maximization

Optimization Results
Parameter Estimates
N Parameter Estimate Approx
Std Err		 t Value Approx
Pr > |t|		 Gradient
Objective
Function
1 sig 108.382690 32.573321 3.327345 0.003540 -3.132469E-9
2 c 2.711476 1.058757 2.560998 0.019108 -0.000000487
3 theta 122.025982 28.692364 4.252908 0.000430 -6.760135E-8


Value of Objective Function = -87.32424712

From inspecting the first- and second-order derivatives at the optimal solution, you can verify that you have obtained an isolated maximum point. The Hessian matrix is shown in Output 6.6.6.

Output 6.6.6 Hessian Matrix
PROC NLP: Nonlinear Maximization

Hessian Matrix
  sig c theta
sig -0.010639963 0.045388887 -0.01003374
c 0.045388887 -4.07872453 -0.083028097
theta -0.01003374 -0.083028097 -0.014752243


Determinant = 0.0000502152


Matrix has Only Negative Eigenvalues

The square roots of the diagonal elements of the approximate covariance matrix of parameter estimates are the approximate standard errors. The covariance matrix is given in Output 6.6.7.

Output 6.6.7 Covariance Matrix
PROC NLP: Nonlinear Maximization

Covariance Matrix 2: H = (NOBS/d) inv(G)
  sig c theta
sig 1060.9795634 29.924959631 -890.0493649
c 29.924959631 1.1209334438 -26.66229938
theta -890.0493649 -26.66229938 823.21458961


Factor sigm = 1


Determinant = 19914.591664


Matrix has 3 Positive Eigenvalue(s)

The difference between the Wald and profile CLs for parameter PHI2 are remarkable, especially for the upper 95% and 99% limits, as shown in Output 6.6.8.

Output 6.6.8 Confidence Limits
PROC NLP: Nonlinear Maximization

Wald and PL Confidence Limits
N Parameter Estimate Alpha Profile Likelihood Confidence
Limits		 Wald Confidence Limits
1 sig 108.382732 0.500000 91.811562 141.564605 86.412310 130.353154
1 sig . 0.100000 76.502373 . 54.804263 161.961200
1 sig . 0.050000 72.215845 . 44.540049 172.225415
1 sig . 0.010000 64.262384 . 24.479224 192.286240
2 c 2.711477 0.500000 2.139297 3.704052 1.997355 3.425599
2 c . 0.100000 1.574162 9.250072 0.969973 4.452981
2 c . 0.050000 1.424853 19.516170 0.636347 4.786607
2 c . 0.010000 1.163096 19.540685 -0.015706 5.438660
3 theta 122.025942 0.500000 91.027144 135.095454 102.673186 141.378698
3 theta . 0.100000 . 141.833769 74.831079 142.985700
3 theta . 0.050000 . 142.512603 65.789795 142.985700
3 theta . 0.010000 . 142.967407 48.119116 142.985700

Previous Page | Next Page | Top of Page

Copyright © SAS Institute, Inc. All Rights Reserved.