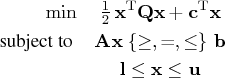The OPTQP Procedure

Overview: OPTQP Procedure

The OPTQP procedure solves quadratic programs - problems with quadratic objective function and a collection of linear constraints, including lower and/or upper bounds on the decision variables.

Mathematically, a quadratic programming (QP) problem can be stated as follows:

$\min & \frac{1}2\, \mathbf{x}^{\rm t} \mathbf{qx} + \mathbf{c}^{\rm t} \mathbf{x... ...} \;\{\ge, =, \le\}\; \mathbf{b} \ & \mathbf{l} \le \mathbf{x} \le \mathbf{u}$

where

$\mathbf{q}$	$\in\mathbb{r}^{nx n}$	is the quadratic (also known as Hessian) matrix
$\mathbf{a}$	$\in\mathbb{r}^{mx n}$	is the constraints matrix
$\mathbf{x}$	$\in\mathbb{r}^n$	is the vector of decision variables
$\mathbf{c}$	$\in\mathbb{r}^n$	is the vector of linear objective function coefficients
$\mathbf{b}$	$\in\mathbb{r}^m$	is the vector of constraints right-hand sides (RHS)
$\mathbf{l}$	$\in\mathbb{r}^n$	is the vector of lower bounds on the decision variables
$\mathbf{u}$	$\in\mathbb{r}^n$	is the vector of upper bounds on the decision variables

The quadratic matrix $\mathbf{q}$ is assumed to be symmetric; i.e.,

$q_{ij} = q_{ji}, \forall i,j = 1, ... , n$

Indeed, it is easy to show that even if $\mathbf{q} \not= \mathbf{q}^{\rm t}$ , the simple modification

$\tilde \mathbf{q} = \frac{1}2(\mathbf{q} + \mathbf{q}^{\rm t})$

produces an equivalent formulation $\mathbf{x}^{\rm t}\mathbf{qx} \equiv \mathbf{x}^{\rm t}{\tilde \mathbf{q}}\mathbf{x};$ hence symmetry is assumed. When specifying a quadratic matrix it suffices to list only lower triangular coefficients.

In addition to being symmetric, $\mathbf{q}$ is also required to be positive semidefinite:

$\mathbf{x}^{\rm t}\mathbf{qx} \ge 0, \forall \mathbf{x}\in\mathbb{r}^n$

for minimization type of models; it is required to be negative semidefinite for the maximization type of models. Convexity can come as a result of a matrix-matrix multiplication

$\mathbf{q} = \mathbf{l}\mathbf{l}^{\rm t}$

or as a consequence of physical laws, etc. See Figure 17.1 for examples of convex, concave, and nonconvex objective functions.

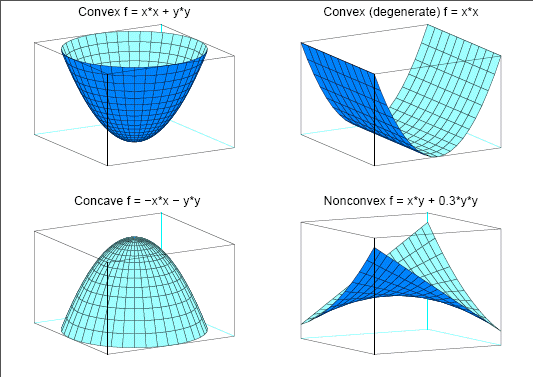
Figure 17.1: Examples of Convex, Concave, and Nonconvex Objective Functions

The order of constraints is insignificant. Some or all components of $\mathbf{l}$ or $\mathbf{u}$ (lower/upper bounds) can be omitted.

Top of Page