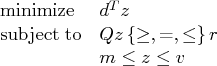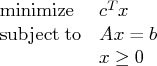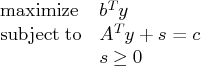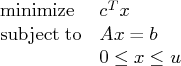| The NETFLOW Procedure |
Linear Programming Models: Interior Point Algorithm
By default, the interior point algorithm is used for problems without a network component, that is, a linear programming problem. You do not need to specify the INTPOINT option in the PROC NETFLOW statement (although you will do no harm if you do).
Data for a linear programming problem resembles the data for side constraints and nonarc variables supplied to PROC NETFLOW when solving a constrained network problem. It is also very similar to the data required by the LP procedure.
Mathematical Description of LP
If the network component of NPSC is removed, the result is the mathematical description of the linear programming problem. If an LP has-
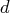 is the
is the 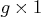 objective function coefficient vector
objective function coefficient vector
-
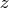 is the
is the 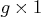 variable value vector
variable value vector
-
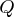 is the
is the 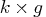 constraint coefficient matrix for
variables, where
constraint coefficient matrix for
variables, where
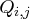 is the coefficient of variable
is the coefficient of variable 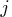 in the
in the 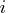 th
constraint
th
constraint
-
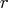 is the
is the 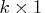 side constraint right-hand-side vector
side constraint right-hand-side vector
-
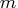 is the
is the 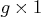 variable value lower bound
vector
variable value lower bound
vector
-
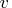 is the
is the 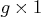 variable
value upper bound vector
variable
value upper bound vector
Interior Point Algorithmic Details
After preprocessing, the linear program to be solved isThere exists an equivalent problem, the dual problem, stated as
The interior point algorithm solves the system of equations to satisfy the Karush-Kuhn-Tucker (KKT) conditions for optimality:
These are the conditions for feasibility, with the
complementarity
condition ![]() added.
Complementarity forces the optimal objectives of the primal and dual
to be equal,
added.
Complementarity forces the optimal objectives of the primal and dual
to be equal, ![]() , as
, as
Before the optimum is reached, a solution ![]() may not satisfy the KKT conditions:
may not satisfy the KKT conditions:
- Primal constraints may be violated,
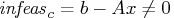 .
.
- Dual constraints may be violated,
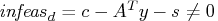 .
.
- Complementarity may not be satisfied,
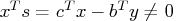 .
This is called the duality gap.
.
This is called the duality gap.
The interior point algorithm works by using Newton's method to find a
direction
to move ![]() from the current solution
from the current solution ![]() toward a better solution:
toward a better solution:
To greatly improve performance, the third equation is changed to
The effect now is to find a direction in which to move to reduce
infeasibilities and to reduce the complementarity toward zero,
but if any
![]() is too close to zero, it is "nudged out" to
is too close to zero, it is "nudged out" to ![]() ,
and any
,
and any
![]() that is larger than
that is larger than ![]() is "nudged into"
is "nudged into" ![]() .
A
.
A ![]() close to or equal to 0.0 biases a direction toward the
optimum,
and a value for
close to or equal to 0.0 biases a direction toward the
optimum,
and a value for ![]() close to or equal to 1.0 "centers" the
direction toward a point where all pairwise products
close to or equal to 1.0 "centers" the
direction toward a point where all pairwise products ![]() .
Such points make up the central path in the interior.
Although centering directions make little, if any, progress in reducing
.
Such points make up the central path in the interior.
Although centering directions make little, if any, progress in reducing
![]() and moving the solution closer to the optimum,
substantial progress toward the optimum can usually be made in
the next iteration.
and moving the solution closer to the optimum,
substantial progress toward the optimum can usually be made in
the next iteration.
The central path is crucial to why the interior point algorithm is so efficient. This path "guides" the algorithm to the optimum through the interior of feasible space. Without centering, the algorithm would find a series of solutions near each other close to the boundary of feasible space. Step lengths along the direction would be small and many more iterations would probably be required to reach the optimum.
That in a nutshell is the primal-dual interior point algorithm.
Varieties of the algorithm differ in the way ![]() and
and ![]() are chosen
and the direction adjusted during each iteration.
A wealth of information can be found in the texts by Roos, Terlaky, and Vial (1997),
Wright (1996), and Ye (1996).
are chosen
and the direction adjusted during each iteration.
A wealth of information can be found in the texts by Roos, Terlaky, and Vial (1997),
Wright (1996), and Ye (1996).
The calculation of the direction is the most time-consuming step
of the interior point algorithm.
Assume the ![]() th iteration is being performed,
so the subscript and superscript
th iteration is being performed,
so the subscript and superscript ![]() can be dropped from the algebra:
can be dropped from the algebra:
Rearranging the third equation,
Equating these two expressions for ![]() and rearranging,
and rearranging,
Substituting into the first direction equation,
The fact that the nonzeros in ![]() have a constant pattern is exploited by all
interior point algorithms, and is a major reason for their
excellent performance.
Before iterations begin,
have a constant pattern is exploited by all
interior point algorithms, and is a major reason for their
excellent performance.
Before iterations begin, ![]() is examined and its rows and
columns are permuted so that during Cholesky Factorization, the number of
fill-ins created is smaller.
A list of arithmetic operations to perform the factorization is saved
in concise computer data structures (working with
memory locations rather than actual numerical values).
This is called symbolic factorization.
During iterations, when memory has been initialized with numerical values,
the operations list is performed sequentially.
Determining how the factorization should be performed again and again
is unnecessary.
is examined and its rows and
columns are permuted so that during Cholesky Factorization, the number of
fill-ins created is smaller.
A list of arithmetic operations to perform the factorization is saved
in concise computer data structures (working with
memory locations rather than actual numerical values).
This is called symbolic factorization.
During iterations, when memory has been initialized with numerical values,
the operations list is performed sequentially.
Determining how the factorization should be performed again and again
is unnecessary.
The Primal-Dual Predictor-Corrector Interior Point Algorithm
The variant of the interior point algorithm implemented in PROC NETFLOW is a Primal-Dual Predictor-Corrector interior point algorithm. At first, Newton's method is used to find a direction to moveComplementarity ![]() is calculated at
is calculated at ![]() and compared with the complementarity at the starting point
and compared with the complementarity at the starting point
![]() , and the success of the affine step is gauged.
If the affine step was successful in reducing the complementarity
by a substantial amount, the need for centering is not great,
and the value of
, and the success of the affine step is gauged.
If the affine step was successful in reducing the complementarity
by a substantial amount, the need for centering is not great,
and the value of ![]() in the following linear system
is assigned a value close to zero.
If, however, the affine step was unsuccessful,
centering would be beneficial,
and the value of
in the following linear system
is assigned a value close to zero.
If, however, the affine step was unsuccessful,
centering would be beneficial,
and the value of ![]() in the following linear system
is assigned a value closer to 1.0.
The value of
in the following linear system
is assigned a value closer to 1.0.
The value of ![]() is therefore adaptively altered depending on the
progress made toward the optimum.
is therefore adaptively altered depending on the
progress made toward the optimum.
A second linear system is solved to determine a centering vector
![]() from
from ![]()
Although the Predictor-Corrector variant entails solving two linear
system instead of one, fewer iterations are usually required to reach
the optimum.
The additional overhead of calculating the second linear system
is small, as the factorization of the
![]() matrix has already been
performed to solve the first linear system.
matrix has already been
performed to solve the first linear system.
Stopping Criteria
There are several reasons why PROC NETFLOW stops interior point optimization. Optimization stops when- the number of iteration equals
MAXITERB=
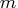
- the relative gap
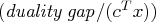 between the primal and
dual objectives is
smaller than the value
of the PDGAPTOL= option,
and both the primal and dual problems are feasible.
Duality gap is defined in the section "Interior Point Algorithmic Details".
between the primal and
dual objectives is
smaller than the value
of the PDGAPTOL= option,
and both the primal and dual problems are feasible.
Duality gap is defined in the section "Interior Point Algorithmic Details".
The reasons to stop optimization outlined in the previous paragraph will be termed the usual stopping conditions in the following explanation.
However, when solving some problems, especially if the problems are large, the usual stopping criteria are inappropriate. PROC NETFLOW might stop prematurely. If it were allowed to perform additional optimization, a better solution would be found. On other occasions, PROC NETFLOW might do too much work. A sufficiently good solution might be reached several iterations before PROC NETFLOW eventually stops.
You can see PROC NETFLOW's progress to the optimum by specifying
PRINTLEVEL2=2.
PROC NETFLOW will produce a table on the SAS log. A row of
the table is generated during each iteration and consists of values of
the affine step
complementarity,
the complementarity of the solution for the next
iteration,
the total bound infeasibility ![]() (see the
(see the
![]() array in the section "Interior Point: Upper Bounds"),
the total constraint infeasibility
array in the section "Interior Point: Upper Bounds"),
the total constraint infeasibility ![]() (see the
(see the
![]() array in the section "Interior Point Algorithmic Details"),
and the total dual infeasibility
array in the section "Interior Point Algorithmic Details"),
and the total dual infeasibility ![]() (see the
(see the
![]() array in the section "Interior Point Algorithmic Details").
As optimization progresses, the values in all columns should converge
to zero.
array in the section "Interior Point Algorithmic Details").
As optimization progresses, the values in all columns should converge
to zero.
To tailor stopping criteria to your problem, you can use two sets of parameters: the STOP_x and the KEEPGOING_x parameters. The STOP_x parameters (STOP_C, STOP_DG, STOP_IB, STOP_IC, and STOP_ID) are used to test for some condition at the beginning of each iteration and if met, to stop immediately. The KEEPGOING_x parameters (KEEPGOING_C, KEEPGOING_DG, KEEPGOING_IB, KEEPGOING_IC, and KEEPGOING_ID) are used when PROC NETFLOW would ordinarily stop but does not if some conditions are not met.
For the sake of conciseness, a set of options will be referred to as the part of the option name they have in common followed by the suffix x. For example, STOP_C, STOP_DG, STOP_IB, STOP_IC, and STOP_ID will collectively be referred to as STOP_x.
At the beginning of each iteration, PROC NETFLOW will test whether
complementarity is ![]() STOP_C (provided you have specified a STOP_C
parameter) and if it is, PROC NETFLOW will stop.
If the duality gap is
STOP_C (provided you have specified a STOP_C
parameter) and if it is, PROC NETFLOW will stop.
If the duality gap is ![]() STOP_DG
(provided you have specified a STOP_DG parameter), PROC NETFLOW will
stop immediately.
This is true as well for the other STOP_x parameters that are related
to infeasibilities, STOP_IB,
STOP_IC, and STOP_ID.
STOP_DG
(provided you have specified a STOP_DG parameter), PROC NETFLOW will
stop immediately.
This is true as well for the other STOP_x parameters that are related
to infeasibilities, STOP_IB,
STOP_IC, and STOP_ID.
For example, if you want PROC NETFLOW to stop optimizing for the usual stopping
conditions, plus the additional condition,
complementarity ![]() 100 or
duality gap
100 or
duality gap ![]() 0.001, then use
0.001, then use
proc netflow stop_c=100 stop_dg=0.001
If you want PROC NETFLOW to stop optimizing for the usual stopping
conditions, plus the additional condition, complementarity ![]() 1000 and
duality gap
1000 and
duality gap ![]() 0.001 and constraint
infeasibility
0.001 and constraint
infeasibility ![]() 0.0001, then use
0.0001, then use
proc netflow
and_stop_c=1000 and_stop_dg=0.01 and_stop_ic=0.0001
Unlike the STOP_x parameters that cause PROC NETFLOW to stop when any one of them is satisfied, the corresponding AND_STOP_x parameters (AND_STOP_C, AND_STOP_DG, AND_STOP_IB, AND_STOP_IC, and AND_STOP_ID) cause PROC NETFLOW to stop only if all (more precisely, all that are specified) options are satisfied. For example, if PROC NETFLOW should stop when
- complementarity
 100 or duality gap
100 or duality gap  0.001 or
0.001 or
- complementarity
 1000 and duality gap
1000 and duality gap  0.001
and constraint infeasibility
0.001
and constraint infeasibility  0.000
0.000
proc netflow
stop_c=100 stop_dg=0.001
and_stop_c=1000 and_stop_dg=0.01 and_stop_ic=0.0001
Just as the STOP_x parameters have AND_STOP_x partners, the KEEPGOING_x parameters have AND_KEEPGOING_x partners. The role of the KEEPGOING_x and AND_KEEPGOING_x parameters is to prevent optimization from stopping too early, even though a usual stopping criterion is met.
When PROC NETFLOW detects that it should stop for a usual stopping condition, it performs the following tests:
- It will test whether complementarity is > KEEPGOING_C (provided you have specified a KEEPGOING_C parameter), and if it is, PROC NETFLOW will perform more optimization.
- Otherwise, PROC NETFLOW will then test whether the primal-dual gap is > KEEPGOING_DG (provided you have specified a KEEPGOING_DG parameter), and if it is, PROC NETFLOW will perform more optimization.
- Otherwise, PROC NETFLOW will then test whether the
total bound infeasibility
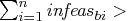 KEEPGOING_IB
(provided you have specified a KEEPGOING_IB parameter), and
if it is, PROC NETFLOW will perform more optimization.
KEEPGOING_IB
(provided you have specified a KEEPGOING_IB parameter), and
if it is, PROC NETFLOW will perform more optimization.
- Otherwise, PROC NETFLOW will then test whether the
total constraint infeasibility
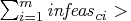 KEEPGOING_IC
(provided you have specified a KEEPGOING_IC parameter), and
if it is, PROC NETFLOW will perform more optimization.
KEEPGOING_IC
(provided you have specified a KEEPGOING_IC parameter), and
if it is, PROC NETFLOW will perform more optimization.
- Otherwise, PROC NETFLOW will then test whether the
total dual infeasibility
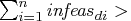 KEEPGOING_ID
(provided you have specified a KEEPGOING_ID parameter), and
if it is, PROC NETFLOW will perform more optimization.
KEEPGOING_ID
(provided you have specified a KEEPGOING_ID parameter), and
if it is, PROC NETFLOW will perform more optimization.
- Otherwise it will test whether complementarity
is > AND_KEEPGOING_C (provided
you have specified an AND_KEEPGOING_C
parameter), and
the primal-dual gap is > AND_KEEPGOING_DG
(provided you have specified an AND_KEEPGOING_DG parameter), and
the total bound infeasibility
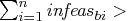 AND_KEEPGOING_IB
(provided you have specified an AND_KEEPGOING_IB parameter), and
the total constraint infeasibility
AND_KEEPGOING_IB
(provided you have specified an AND_KEEPGOING_IB parameter), and
the total constraint infeasibility 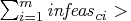 AND_KEEPGOING_IC (provided you have specified an AND_KEEPGOING_IC
parameter) and
the total dual infeasibility
AND_KEEPGOING_IC (provided you have specified an AND_KEEPGOING_IC
parameter) and
the total dual infeasibility 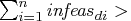 AND_KEEPGOING_ID
(provided you have specified an AND_KEEPGOING_ID parameter), and
if it is, PROC NETFLOW will perform more optimization.
AND_KEEPGOING_ID
(provided you have specified an AND_KEEPGOING_ID parameter), and
if it is, PROC NETFLOW will perform more optimization.
If all these tests to decide whether more optimization should be performed are false, optimization is stopped.
For example,
proc netflow
stop_c=1000
and_stop_c=2000 and_stop_dg=0.01
and_stop_ib=1 and_stop_ic=1 and_stop_id=1
keepgoing_c=1500
and_keepgoing_c=2500 and_keepgoing_dg=0.05
and_keepgoing_ib=1 and_keepgoing_ic=1 and_keepgoing_id=1
At the beginning of each iteration, PROC NETFLOW will stop if
- complementarity
 1000 or
1000 or
- complementarity
 2000 and
duality gap
2000 and
duality gap  0.01 and the total
bound, constraint, and dual infeasibilities are each
0.01 and the total
bound, constraint, and dual infeasibilities are each  1
1
When PROC NETFLOW determines it should stop because a usual stopping condition is met, it will stop only if
- complementarity
 1500 or
1500 or
- complementarity
 2500 and
duality gap
2500 and
duality gap  0.05 and the total bound, constraint, and dual infeasibilities are each
0.05 and the total bound, constraint, and dual infeasibilities are each  1
1
Interior Point: Upper Bounds
If the LP model had upper bounds (The primal linear program to be solved is
where ![]() is split into
is split into ![]() and
and ![]() . Let
. Let ![]() be
primal slack so that
be
primal slack so that ![]() , and associate dual variables
, and associate dual variables ![]() with these constraints.
The interior point algorithm solves the system of equations to
satisfy the Karush-Kuhn-Tucker (KKT) conditions for optimality:
with these constraints.
The interior point algorithm solves the system of equations to
satisfy the Karush-Kuhn-Tucker (KKT) conditions for optimality:
These are the conditions for feasibility, with the
complementarity
conditions ![]() and
and ![]() added.
Complementarity forces the optimal objectives of the primal and dual
to be equal,
added.
Complementarity forces the optimal objectives of the primal and dual
to be equal, ![]() , as
, as
Before the optimum is reached, a solution ![]() might not satisfy the KKT conditions:
might not satisfy the KKT conditions:
- Primal bound constraints may be violated,
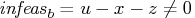 .
.
- Primal constraints may be violated,
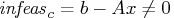 .
. - Dual constraints may be violated,
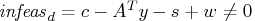 .
. - Complementarity conditions may not be satisfied,
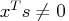 and
and 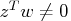 .
.
The calculations of the interior point algorithm can easily be derived in a
fashion similar to calculations for when an LP has no upper bounds.
See the paper by Lustig, Marsten, and Shanno (1992).
An important point is that upper bounds can be handled by specializing
the algorithm and not by generating the constraints ![]() and adding these to the main primal constraints
and adding these to the main primal constraints ![]() .
.
Getting Started: Linear Programming Models: Interior Point Algorithm
To solve linear programming problem using PROC NETFLOW, you save a representation of the variables and the constraints in one or two SAS data sets. These data sets are then passed to PROC NETFLOW for solution. There are various forms that a problem's data can take. You can use any one or a combination of several of these forms.The ARCDATA= data set contains information about the variables of the problem. Although this data set is called ARCDATA, it contains data for no arcs. Instead, all data in this data set are related to variables.
The ARCDATA= data set can be used to specify information about
variables, including objective function coefficients,
lower and upper value bounds, and names.
These data are the elements of the vectors
![]() ,
, ![]() , and
, and ![]() in problem (NPSC).
Data for a variable can be given in more than
one observation.
in problem (NPSC).
Data for a variable can be given in more than
one observation.
When the data for a constrained network problem is being provided, the ARCDATA= data set always contains information necessary for arcs, their tail and head nodes, and optionally the supply and demand information of these nodes. When the data for a linear programming problem is being provided, none of this information is present, as the model has no arcs. This is the way PROC NETFLOW decides which type of problem it is to solve.
PROC NETFLOW was originally designed to solve models with networks, so an ARCDATA= data set is always expected. If an ARCDATA= data set is not specified, by default the last data set created before PROC NETFLOW is invoked is assumed to be an ARCDATA= data set. However, these characteristics of PROC NETFLOW are not helpful when a linear programming problem is being solved and all data is provided in a single data set specified by the CONDATA= data set, and that data set is not the last data set created before PROC NETFLOW starts. In this case, you must specify that an ARCDATA= data set and a CONDATA= data set are both equal to the input data set. PROC NETFLOW then knows that a linear programming problem is to be solved, and the data reside in one data set.
The CONDATA= data set describes
the constraints and
their right-hand sides. These data are elements of the matrix
![]() and
the vector
and
the vector ![]() .
.
Constraint types are also specified in the CONDATA= data set. You can include in this data set variable data such as upper bound values, lower value bounds, and objective function coefficients. It is possible to give all information about some or all variables in the CONDATA= data set.
A variable is identified in this data set by its name. If you specify a variable's name in the ARCDATA= data set, then this name is used to associate data in the CONDATA= data set with that variable.
If you use the dense constraint input format, these variable names are names of SAS variables in the VAR list of the CONDATA= data set.
If you use the sparse constraint input format, these variable names are values of the COLUMN list SAS variable of CONDATA= data set.
When using the interior point algorithm, the execution of PROC NETFLOW has two stages. In the preliminary (zeroth) stage, the data are read from the ARCDATA= data set (if used) and the CONDATA= data set. Error checking is performed. In the next stage, the linear program is preprocessed, then the optimal solution to the linear program is found. The solution is saved in the CONOUT= data set. This data set is also named in the PROC NETFLOW, RESET, and SAVE statements.
See the section "Getting Started: Network Models: Interior Point Algorithm" for a fuller description of the stages of the interior point algorithm.
Introductory Example: Linear Programming Models: Interior Point Algorithm
Consider the linear programming problem in the section "An Introductory Example" in the chapter on the LP procedure.
data dcon1;
input _id_ $17.
a_light a_heavy brega naphthal naphthai
heatingo jet_1 jet_2
_type_ $ _rhs_;
datalines;
profit -175 -165 -205 0 0 0 300 300 max .
naphtha_l_conv .035 .030 .045 -1 0 0 0 0 eq 0
naphtha_i_conv .100 .075 .135 0 -1 0 0 0 eq 0
heating_o_conv .390 .300 .430 0 0 -1 0 0 eq 0
recipe_1 0 0 0 0 .3 .7 -1 0 eq 0
recipe_2 0 0 0 .2 0 .8 0 -1 eq 0
available 110 165 80 . . . . . upperbd .
;
To find the minimum cost solution and to examine all or parts of the optimum, you use PRINT statements.
- print problem/short; outputs information for all variables and all constraint coefficients. See Figure 5.19 and Figure 5.20.
- print some_variables(j:)/short; is information about a set of variables, (in this case, those with names that start with the character string preceding the colon). See Figure 5.21.
- print some_cons(recipe_1)/short; is information about a set of constraints (here, that set only has one member, the constraint called recipe_1). See Figure 5.22.
- print con_variables(_all_,brega)/short; lists the constraint information for a set of variables (here, that set only has one member, the variable called brega). See Figure 5.23.
- print con_variables(recipe:,n: jet_1)/short; coefficient information for those in a set of constraints belonging to a set of variables. See Figure 5.24.
proc netflow
condata=dcon1
conout=solutn1;
run;
print problem/short;
print some_variables(j:)/short;
print some_cons(recipe_1)/short;
print con_variables(_all_,brega)/short;
print con_variables(recipe:,n: jet_1)/short;
The following messages, which appear on the SAS log, summarize the model as read by PROC NETFLOW and note the progress toward a solution:
NOTE: Number of variables= 8 .
NOTE: Number of <= constraints= 0 .
NOTE: Number of == constraints= 5 .
NOTE: Number of >= constraints= 0 .
NOTE: Number of constraint coefficients= 18 .
NOTE: After preprocessing, number of <= constraints= 0.
NOTE: After preprocessing, number of == constraints= 0.
NOTE: After preprocessing, number of >= constraints= 0.
NOTE: The preprocessor eliminated 5 constraints from the
problem.
NOTE: The preprocessor eliminated 18 constraint
coefficients from the problem.
NOTE: After preprocessing, number of variables= 0.
NOTE: The preprocessor eliminated 8 variables from the
problem.
WARNING: Optimization is unnecessary as the problem no
longer has any variables and rows.
NOTE: Preprocessing could have caused that.
NOTE: Objective= 1544.
NOTE: The data set WORK.SOLUTN1 has 8 observations and
6 variables.
Figure 5.19: PRINT PROBLEM/SHORT;
Figure 5.20: PRINT PROBLEM/SHORT; (continued)
Figure 5.21: PRINT SOME_VARIABLES(J:)/SHORT;
Figure 5.22: PRINT SOME_CONS(RECIPE_1)/SHORT;
Figure 5.23: PRINT CON_VARIABLES(_ALL_,BREGA)/SHORT;
Figure 5.24: PRINT CON_VARIABLES(RECIPE:,N: JET_1)/SHORT;
Unlike PROC LP, which displays the solution and other information as output, PROC NETFLOW saves the optimum in output SAS data sets you specify. For this example, the solution is saved in the SOLUTN1 data set. It can be displayed with PROC PRINT as
proc print data=solutn1;
var _name_ _objfn_ _upperbd _lowerbd _value_ _fcost_;
sum _fcost_;
title3 'LP Optimum';
run;
Notice, in the CONOUT=SOLUTN1 (Figure 5.25), the optimal value
through each variable in the linear program
is given in the variable named _VALUE_, and the cost of value
for each variable is given in the variable _FCOST_.
| LP Optimum |
| Obs | _NAME_ | _OBJFN_ | _UPPERBD | _LOWERBD | _VALUE_ | _FCOST_ |
|---|---|---|---|---|---|---|
| 1 | a_heavy | -165 | 165 | 0 | 0.00 | 0 |
| 2 | a_light | -175 | 110 | 0 | 110.00 | -19250 |
| 3 | brega | -205 | 80 | 0 | 80.00 | -16400 |
| 4 | heatingo | 0 | 99999999 | 0 | 77.30 | 0 |
| 5 | jet_1 | 300 | 99999999 | 0 | 60.65 | 18195 |
| 6 | jet_2 | 300 | 99999999 | 0 | 63.33 | 18999 |
| 7 | naphthai | 0 | 99999999 | 0 | 21.80 | 0 |
| 8 | naphthal | 0 | 99999999 | 0 | 7.45 | 0 |
| 1544 |
Figure 5.25: CONOUT=SOLUTN1
The same model can be specified in the sparse format as in the following scon2 dataset. This format enables you to omit the zero coefficients.
data scon2;
format _type_ $8. _col_ $8. _row_ $16. ;
input _type_ $ _col_ $ _row_ $ _coef_;
datalines;
max . profit .
eq . napha_l_conv .
eq . napha_i_conv .
eq . heating_oil_conv .
eq . recipe_1 .
eq . recipe_2 .
upperbd . available .
. a_light profit -175
. a_light napha_l_conv .035
. a_light napha_i_conv .100
. a_light heating_oil_conv .390
. a_light available 110
. a_heavy profit -165
. a_heavy napha_l_conv .030
. a_heavy napha_i_conv .075
. a_heavy heating_oil_conv .300
. a_heavy available 165
. brega profit -205
. brega napha_l_conv .045
. brega napha_i_conv .135
. brega heating_oil_conv .430
. brega available 80
. naphthal napha_l_conv -1
. naphthal recipe_2 .2
. naphthai napha_i_conv -1
. naphthai recipe_1 .3
. heatingo heating_oil_conv -1
. heatingo recipe_1 .7
. heatingo recipe_2 .8
. jet_1 profit 300
. jet_1 recipe_1 -1
. jet_2 profit 300
. jet_2 recipe_2 -1
;
To find the minimum cost solution, invoke PROC NETFLOW (note the SPARSECONDATA option which must be specified) as follows:
proc netflow
sparsecondata
condata=scon2
conout=solutn2;
run;
A data set that is used as an ARCDATA= data set can be initialized as follows:
data vars3;
input _name_ $ profit available;
datalines;
a_heavy -165 165
a_light -175 110
brega -205 80
heatingo 0 .
jet_1 300 .
jet_2 300 .
naphthai 0 .
naphthal 0 .
;
The following CONDATA= data set is the original dense format CONDATA= dcon1 data set with the variable information removed. (You could have left some or all of that information in CONDATA as PROC NETFLOW "merges" data, but doing that and checking for consistency uses time.)
data dcon3;
input _id_ $17.
a_light a_heavy brega naphthal naphthai
heatingo jet_1 jet_2
_type_ $ _rhs_;
datalines;
naphtha_l_conv .035 .030 .045 -1 0 0 0 0 eq 0
naphtha_i_conv .100 .075 .135 0 -1 0 0 0 eq 0
heating_o_conv .390 .300 .430 0 0 -1 0 0 eq 0
recipe_1 0 0 0 0 .3 .7 -1 0 eq 0
recipe_2 0 0 0 .2 0 .8 0 -1 eq 0
;
It is important to note that it is now necessary to specify the MAXIMIZE option; otherwise, PROC NETFLOW will optimize to the minimum (which, incidently, has a total objective = -3539.25). You must indicate that the SAS variable profit in the ARCDATA=vars3 data set has values that are objective function coefficients, by specifying the OBJFN statement. The UPPERBD must be specified as the SAS variable available that has as values upper bounds.
proc netflow
maximize /* ***** necessary ***** */
arcdata=vars3
condata=dcon3
conout=solutn3;
objfn profit;
upperbd available;
run;
The ARCDATA=vars3 data set can become more concise by noting that the model variables heatingo, naphthai, and naphthal have zero objective function coefficients (the default) and default upper bounds, so those observations need not be present.
data vars4;
input _name_ $ profit available;
datalines;
a_heavy -165 165
a_light -175 110
brega -205 80
jet_1 300 .
jet_2 300 .
;
The CONDATA=dcon3 data set can become more concise by noting that all the constraints have the same type (eq) and zero (the default) rhs values. This model is a good candidate for using the DEFCONTYPE= option.
The DEFCONTYPE= option
can be useful not only when
all constraints have the same type as is the case here, but also
when most constraints have the same type, or if you prefer
to change the default type from ![]() to = or
to = or ![]() .
The essential constraint type data in
CONDATA= data set is that which overrides the
DEFCONTYPE= type you specified.
.
The essential constraint type data in
CONDATA= data set is that which overrides the
DEFCONTYPE= type you specified.
data dcon4;
input _id_ $17.
a_light a_heavy brega naphthal naphthai
heatingo jet_1 jet_2;
datalines;
naphtha_l_conv .035 .030 .045 -1 0 0 0 0
naphtha_i_conv .100 .075 .135 0 -1 0 0 0
heating_o_conv .390 .300 .430 0 0 -1 0 0
recipe_1 0 0 0 0 .3 .7 -1 0
recipe_2 0 0 0 .2 0 .8 0 -1
;
proc netflow
maximize defcontype=eq
arcdata=vars3
condata=dcon3
conout=solutn3;
objfn profit;
upperbd available;
run;
Several different ways of using an ARCDATA=
data set
and a sparse format
CONDATA= data set for this
linear program follow.
The following CONDATA= data set is the result of
removing the profit and available data from the original
sparse format CONDATA=scon2 data set.
data scon5;
format _type_ $8. _col_ $8. _row_ $16. ;
input _type_ $ _col_ $ _row_ $ _coef_;
datalines;
eq . napha_l_conv .
eq . napha_i_conv .
eq . heating_oil_conv .
eq . recipe_1 .
eq . recipe_2 .
. a_light napha_l_conv .035
. a_light napha_i_conv .100
. a_light heating_oil_conv .390
. a_heavy napha_l_conv .030
. a_heavy napha_i_conv .075
. a_heavy heating_oil_conv .300
. brega napha_l_conv .045
. brega napha_i_conv .135
. brega heating_oil_conv .430
. naphthal napha_l_conv -1
. naphthal recipe_2 .2
. naphthai napha_i_conv -1
. naphthai recipe_1 .3
. heatingo heating_oil_conv -1
. heatingo recipe_1 .7
. heatingo recipe_2 .8
. jet_1 recipe_1 -1
. jet_2 recipe_2 -1
;
proc netflow
maximize
sparsecondata
arcdata=vars3 /* or arcdata=vars4 */
condata=scon5
conout=solutn5;
objfn profit;
upperbd available;
run;
The CONDATA=scon5 data set can become more concise by noting that all the constraints have the same type (eq) and zero (the default) rhs values. Use the DEFCONTYPE= option again. Once the first 5 observations of the CONDATA=scon5 data set are removed, the _type_ SAS variable has values that are missing in the remaining observations. Therefore, this SAS variable can be removed.
data scon6;
input _col_ $ _row_&$16. _coef_;
datalines;
a_light napha_l_conv .035
a_light napha_i_conv .100
a_light heating_oil_conv .390
a_heavy napha_l_conv .030
a_heavy napha_i_conv .075
a_heavy heating_oil_conv .300
brega napha_l_conv .045
brega napha_i_conv .135
brega heating_oil_conv .430
naphthal napha_l_conv -1
naphthal recipe_2 .2
naphthai napha_i_conv -1
naphthai recipe_1 .3
heatingo heating_oil_conv -1
heatingo recipe_1 .7
heatingo recipe_2 .8
jet_1 recipe_1 -1
jet_2 recipe_2 -1
;
proc netflow
maximize
defcontype=eq
sparsecondata
arcdata=vars3 /* or arcdata=vars4 */
condata=scon6
conout=solutn6;
objfn profit;
upperbd available;
run;
Interactivity: Linear Programming Models: Interior Point algorithm
PROC NETFLOW can be used interactively. You begin by giving the PROC NETFLOW statement, and you must specify the CONDATA= data set. If necessary, specify the ARCDATA= data set.The variable lists should be given next. If you have variables in the input data sets that have special names (for example, a variable in the ARCDATA= data set named _COST_ that has objective function coefficients as values), it may not be necessary to have many or any variable lists.
The PRINT, QUIT, SAVE, SHOW, RESET, and RUN statements follow and can be listed in any order. The QUIT statements can be used only once. The others can be used as many times as needed.
The CONOPT and PIVOT are not relevant to the interior point algorithm and should not be used.
Use the RESET or SAVE statement to change the name of the output data set. There is only one output data set, the CONOUT= data set. With the RESET statement, you can also indicate the reasons why optimization should stop, (for example, you can indicate the maximum number of iterations that can be performed). PROC NETFLOW then has a chance to either execute the next statement or, if the next statement is one that PROC NETFLOW does not recognize (the next PROC or DATA step in the SAS session), do any allowed optimization and finish. If no new statement has been submitted, you are prompted for one. Some options of the RESET statement enable you to control aspects of the interior point algorithm. Specifying certain values for these options can reduce the time it takes to solve a problem. Note that any of the RESET options can be specified in the PROC NETFLOW statement.
The RUN statement starts optimization. Once the optimization has started, it runs until the optimum is reached. The RUN statement should be specified at most once.
The QUIT statement immediately stops PROC NETFLOW. The SAVE statement has options that enable you to name the output data set; information about the current solution is saved in this output data set. Use the SHOW statement if you want to examine the values of options of other statements. Information about the amount of optimization that has been done and the STATUS of the current solution can also be displayed using the SHOW statement.
The PRINT statement instructs PROC NETFLOW to display parts of the problem. The ways the PRINT statements are specified are identical whether the interior point algorithm or the simplex algorithm is used; however, there are minor differences in what is displayed for each variable or constraint coefficient.
PRINT VARIABLES produces information on all arcs. PRINT SOME_VARIABLES limits this output to a subset of variables. There are similar PRINT statements for constraints:
PRINT CONSTRAINTS; PRINT SOME_CONS;PRINT CON_VARIABLES enables you to limit constraint information that is obtained to members of a set of variables that have nonzero constraint coefficients in a set of constraints.
For example, an interactive PROC NETFLOW run might look something like this:
proc netflow
condata=data set
other options;
variable list specifications; /* if necessary */
reset options;
print options; /* look at problem */
run; /* do some optimization */
print options; /* look at the optimal solution */
save options; /* keep optimal solution */
If you are interested only in finding the optimal solution, have used SAS variables that have special names in the input data sets, and want to use default setting for everything, then the following statement is all you need:
- proc netflow condata= data set ;
Functional Summary: Linear Programming Models: Interior Point Algorithm
The following table outlines the options available for the NETFLOW procedure when the interior point algorithm is being used to solve a linear programming problem, classified by function. Table 5.8: Functional Summary, Linear Programming Models| Description | Statement | Option |
| Input Data Set Options: | ||
| arcs input data set | PROC NETFLOW | ARCDATA= |
| constraint input data set | PROC NETFLOW | CONDATA= |
| Output Data Set Option: | ||
| solution data set | PROC NETFLOW | CONOUT= |
| Data Set Read Options: | ||
| CONDATA has sparse data format | PROC NETFLOW | SPARSECONDATA |
| default constraint type | PROC NETFLOW | DEFCONTYPE= |
| special COLUMN variable value | PROC NETFLOW | TYPEOBS= |
| special COLUMN variable value | PROC NETFLOW | RHSOBS= |
| data for a constraint found once in CONDATA | PROC NETFLOW | CON_SINGLE_OBS |
| data for a coefficient found once in CONDATA | PROC NETFLOW | NON_REPLIC= |
| data is grouped, exploited during data read | PROC NETFLOW | GROUPED= |
| Problem Size Specification Options: | ||
| approximate number of variables | PROC NETFLOW | NNAS= |
| approximate number of coefficients | PROC NETFLOW | NCOEFS= |
| approximate number of constraints | PROC NETFLOW | NCONS= |
| Network Options: | ||
| default variable objective function coefficient | PROC NETFLOW | DEFCOST= |
| default variable upper bound | PROC NETFLOW | DEFCAPACITY= |
| default variable lower bound | PROC NETFLOW | DEFMINFLOW= |
| Memory Control Options: | ||
| issue memory usage messages to SAS log | PROC NETFLOW | MEMREP |
| number of bytes to use for main memory | PROC NETFLOW | BYTES= |
| proportion of memory for arrays | PROC NETFLOW | COREFACTOR= |
| maximum bytes for a single array | PROC NETFLOW | MAXARRAYBYTES= |
| Interior Point Algorithm Options: | ||
| use interior point algorithm | PROC NETFLOW | INTPOINT |
| factorization method | RESET | FACT_METHOD= |
| allowed amount of dual infeasibility | RESET | TOLDINF= |
| allowed amount of primal infeasibility | RESET | TOLPINF= |
| allowed total amount of dual infeasibility | RESET | TOLTOTDINF= |
| allowed total amount of primal infeasibility | RESET | TOLTOTPINF= |
| cut-off tolerance for Cholesky factorization | RESET | CHOLTINYTOL= |
| density threshold for Cholesky processing | RESET | DENSETHR= |
| step-length multiplier | RESET | PDSTEPMULT= |
| preprocessing type | RESET | PRSLTYPE= |
| print optimization progress on SAS log | RESET | PRINTLEVEL2= |
| write optimization time to SAS log | RESET | OPTIM_TIMER |
| Interior Point Stopping Criteria Options: | ||
| maximum number of interior point iterations | RESET | MAXITERB= |
| primal-dual (duality) gap tolerance | RESET | PDGAPTOL= |
| stop because of complementarity | RESET | STOP_C= |
| stop because of duality gap | RESET | STOP_DG= |
| stop because of | RESET | STOP_IB= |
| stop because of | RESET | STOP_IC= |
| stop because of | RESET | STOP_ID= |
| stop because of complementarity | RESET | AND_STOP_C= |
| stop because of duality gap | RESET | AND_STOP_DG= |
| stop because of | RESET | AND_STOP_IB= |
| stop because of | RESET | AND_STOP_IC= |
| stop because of | RESET | AND_STOP_ID= |
| stop because of complementarity | RESET | KEEPGOING_C= |
| stop because of duality gap | RESET | KEEPGOING_DG= |
| stop because of | RESET | KEEPGOING_IB= |
| stop because of | RESET | KEEPGOING_IC= |
| stop because of | RESET | KEEPGOING_ID= |
| stop because of complementarity | RESET | AND_KEEPGOING_C= |
| stop because of duality gap | RESET | AND_KEEPGOING_DG= |
| stop because of | RESET | AND_KEEPGOING_IB= |
| stop because of | RESET | AND_KEEPGOING_IC= |
| stop because of | RESET | AND_KEEPGOING_ID= |
| PRINT Statement Options: | ||
| display everything | PROBLEM | |
| display variable information | VARIABLES | |
| display constraint information | CONSTRAINTS | |
| display information for some variables | SOME_VARIABLES | |
| display information for some constraints | SOME_CONS | |
| display information for some constraints associated with some variables | CON_VARIABLES | |
| PRINT Statement Qualifiers: | ||
| produce a short report | / SHORT | |
| produce a long report | / LONG | |
| display arcs/variables with zero flow/value | / ZERO | |
| display arcs/variables with nonzero flow/value | / NONZERO | |
| SHOW Statement Options: | ||
| show problem, optimization status | SHOW | STATUS |
| show LP model parameters | SHOW | NETSTMT |
| show data sets that have been or will be created | SHOW | DATASETS |
| Miscellaneous Options: | ||
| infinity value | PROC NETFLOW | INFINITY= |
| scale constraint row, variable column coefficients, or both | PROC NETFLOW | SCALE= |
| maximization instead of minimization | PROC NETFLOW | MAXIMIZE |
Dictionary of Options: Linear Programming Models, Interior Point Algorithm
| AND_KEEPGOING_C= | AND_KEEPGOING_DG= | AND_KEEPGOING_IB= |
| AND_KEEPGOING_IC= | AND_KEEPGOING_ID= | AND_STOP_C= |
| AND_STOP_DG= | AND_STOP_IB= | AND_STOP_IC= |
| AND_STOP_ID= | BYTES= | CAPACITY Statement |
| CHOLTINYTOL= | COEF Statement | COLUMN Statement |
| CONDATA= | CONOUT= | CONSTRAINTS |
| CON_VARIABLES | COREFACTOR= | COST Statement |
| DEFCAPACITY= | DEFCONTYPE= | DEFCOST= |
| DEFMINFLOW= | DENSETHR= | ID Statement |
| INFINITY= | INTPOINT | KEEPGOING_C= |
| KEEPGOING_DG= | KEEPGOING_IB= | KEEPGOING_IC= |
| KEEPGOING_ID= | LO Statement | MAXARRAYBYTES= |
| MAXIMIZE | MAXITERB= | MEMREP |
| NAME Statement | NCOEFS= | NCONS= |
| NNAS= | PDGAPTOL= | PDSTEPMULT= |
| PRINT Statement | PRINTLEVEL2= | PROBLEM |
| PRSLTYPE= | QUIT Statement | RESET Statement |
| RHS Statement | RHSOBS= | ROW Statement |
| RUN Statement | SAVE Statement | SCALE= |
| SHOW Statement | SOME_CONS | SOME_VARIABLES |
| SPARSECONDATA | STOP_C= | STOP_DG= |
| STOP_IB= | STOP_IC= | STOP_ID= |
| TOLDINF= | TOLPINF= | TOLTOTDINF= |
| TOLTOTPINF= | TYPE Statement | TYPEOBS= |
| VAR Statement | VARIABLES | VERBOSE= |
Copyright © 2008 by SAS Institute Inc., Cary, NC, USA. All rights reserved.