The Mixed Integer Linear Programming Solver: Controlling the Branch-and-Bound Algorithm :: SAS/OR(R) 9.2 User's Guide: Mathematical Programming

The Mixed Integer Linear Programming Solver

Controlling the Branch-and-Bound Algorithm

There are numerous strategies that can be used to control the branch-and-bound search (see Linderoth and Savelsbergh 1998, Achterberg, Koch, and Martin 2005). The MILP solver in PROC OPTMODEL implements the most widely used strategies and provides several options that enable you to direct the choice of the next active node and of the branching variable. In the discussion that follows, let ( ${lp}^k$ ) be the linear programming relaxation of subproblem ( ${milp}^k$ ). Also, let

$f_i(k)= \bar{x}^k_i-\lfloor \bar{x}^k_i \rfloor$

where $\bar{x}^k$ is the optimal solution to the relaxation problem ( ${lp}^k$ ) solved at node

Node Selection

The NODESEL= option specifies the strategy used to select the next active node. The valid keywords for this option are AUTOMATIC, BESTBOUND, BESTESTIMATE, and DEPTH. The following list describes the strategy associated with each keyword.

AUTOMATIC: enables the MILP solver to choose the best node selection strategy based on problem characteristics and search progress. This is the default setting.
BESTBOUND: chooses the node with the smallest (or largest, in the case of a maximization problem) relaxed objective value. The best-bound strategy tends to reduce the number of nodes to be processed and can improve lower bounds quickly. If there is no good upper bound, however, the number of active nodes can be large. This can result in the solver running out of memory.
BESTESTIMATE: chooses the node with the smallest (or largest, in the case of a maximization problem) objective value of the estimated integer solution. Besides improving lower bounds, the best-estimate strategy also attempts to process nodes that can yield good feasible solutions.
DEPTH: chooses the node that is deepest in the search tree. Depth-first search is effective in locating feasible solutions, since such solutions are usually deep in the search tree. Compared to the costs of the best-bound and best-estimate strategies, the cost of solving LP relaxations is less in the depth-first strategy. The number of active nodes is generally small, but it is possible that the depth-first search will remain in a portion of the search tree with no good integer solutions. This occurrence is computationally expensive.

Variable Selection

The VARSEL= option specifies the strategy used to select the next branching variable. The valid keywords for this option are AUTOMATIC, MAXINFEAS, MININFEAS, PSEUDO, and STRONG. The following list describes the action taken in each case when $\bar{x}^k$ , a relaxed optimal solution of ( ${milp}^k$ ), is used to define two active subproblems. In the following list, "INTTOL" refers to the value assigned using the INTTOL= option. For details about the INTTOL= option, see the section "Control Options".

AUTOMATIC

enables the MILP solver to choose the best variable selection strategy based on problem characteristics and search progress. This is the default setting.

MAXINFEAS

chooses as the branching variable the variable

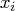such that

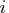maximizes

$\{\min \{f_i(k), 1 - f_i(k)\} | i\in {\cal s} {\rmand}$

${inttol} \leq f_i(k) \leq 1- {inttol} \}$

MININFEAS

chooses as the branching variable the variable

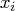such that

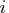minimizes

$\{\min \{f_i(k), 1 - f_i(k)\} | i\in {\cal s} {\rmand}$

${inttol} \leq f_i(k) \leq 1- {inttol} \}$

PSEUDO

chooses as the branching variable the variable

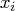such that

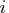maximizes the weighted up and down pseudocosts. Pseudocost branching attempts to branch on significant variables first, quickly improving lower bounds. Pseudocost branching estimates significance based on historical information; however, this approach might not be accurate for future search.

STRONG

chooses as the branching variable the variable

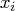such that

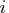maximizes the estimated improvement in the objective value. Strong branching first generates a list of candidates, then branches on each candidate and records the improvement in the objective value. The candidate with the largest improvement is chosen as the branching variable. Strong branching can be effective for combinatorial problems, but it is usually computationally expensive.

Branching Priorities

In some cases, it is possible to speed up the branch-and-bound algorithm by branching on variables in a specific order. You can accomplish this in PROC OPTMODEL by attaching branching priorities to the integer variables in your model by using the .priority suffix. More information about this suffix is available in the section "Integer Variable Suffixes" in Chapter 6. For an example in which branching priorities are used, see Example 9.3.

Top of Page