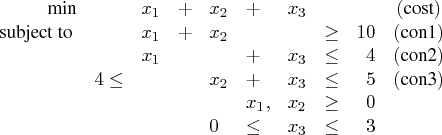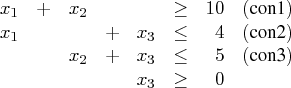The Linear Programming Solver

Example 8.4: Finding an Irreducible Infeasible Set

This example demonstrates the use of the experimental IIS= option to locate an irreducible infeasible set. Suppose you want to solve a linear program that has the following simple formulation:

It is easy to verify that the following three constraints (or rows) and one variable (or column) bound form an IIS for this problem:

You can formulate the problem and call the LP solver by using the following statements:

    proc optmodel presolver=none;
       /* declare variables */
       var x{1..3} >=0;
       
       /* upper bound on variable x[3] */
       x[3].ub = 3;
       
       /* objective function */
       min obj = x[1] + x[2] + x[3];
       
       /* constraints */
       con c1: x[1] + x[2] >= 10;
       con c2: x[1] + x[3] <= 4;
       con c3: 4 <= x[2] + x[3] <= 5;
       
       solve with lp / iis = on;
       
       print x.status;
       print c1.status c2.status c3.status;
 

The notes printed in the log appear in Output 8.4.1.

Output 8.4.1: Finding an IIS: Log

NOTE: The problem has 3 variables (0 free, 0 fixed). NOTE: The problem has 3 linear constraints (1 LE, 0 EQ, 1 GE, 1 range). NOTE: The problem has 6 linear constraint coefficients. NOTE: The problem has 0 nonlinear constraints (0 LE, 0 EQ, 0 GE, 0 range). NOTE: The IIS option is called. NOTE: Objective Phase Iteration Value 1 1 5.000000 1 2 1.000000 NOTE: Processing rows. 1 3 0 1 4 0 1 6 1.000000 NOTE: Processing columns. 1 7 0 NOTE: The IIS option found an IIS set with 3 rows and 1 columns.

The output of the PRINT statements appears in Output 8.4.2. The value of the .status suffix for the variables x[1] and x[2] is "I," which indicates an infeasible problem. The value I is not one of those assigned by the IIS= option to members of the IIS, however, so the variable bounds for x[1] and x[2] are not in the IIS.

Output 8.4.2: Solution Summary,Variable Status,and Constraint Status

Solution Summary Solver Dual Simplex Objective Function obj Solution Status Infeasible Objective Value . Iterations 7 [1] x.STATUS 1   2   3 I_L c1.STATUS c2.STATUS c3.STATUS I_L I_U I_U

The value of c3.status is I_U, which indicates that is an element of the IIS. The original constraint is c3, a range constraint with a lower bound of 4. If you choose to remove the constraint , you can change the value of c3.ub to the largest positive number representable in your operating environment. You can specify this number by using the MIN aggregation expression in the OPTMODEL procedure. See "MIN Aggregation Expression" for details.

The modified LP problem is specified and solved by adding the following lines to the original PROC OPTMODEL call.

       /* relax upper bound on constraint c3 */
       c3.ub = min{{}}0;
       
       solve with lp / iis = on;
       
       /* print solution */
       print x;
 

Because one element of the IIS has been removed, the modified LP problem should no longer contain the infeasible set. Due to the size of this problem, there should be no additional irreducible infeasible sets.

The notes shown in Output 8.4.3 are printed to the log.

Output 8.4.3: Infeasibility Removed: Log

NOTE: The problem has 3 variables (0 free, 0 fixed). NOTE: The problem has 3 linear constraints (1 LE, 0 EQ, 2 GE, 0 range). NOTE: The problem has 6 linear constraint coefficients. NOTE: The problem has 0 nonlinear constraints (0 LE, 0 EQ, 0 GE, 0 range). NOTE: The IIS option is called. NOTE: Objective Phase Iteration Value 1 2 0 NOTE: The IIS option found this problem to be feasible. NOTE: The OPTLP presolver value AUTOMATIC is applied. NOTE: The OPTLP presolver removed 0 variables and 0 constraints. NOTE: The OPTLP presolver removed 0 constraint coefficients. NOTE: The presolved problem has 3 variables, 3 constraints, and 6 constraint coefficients. NOTE: The DUAL SIMPLEX solver is called. NOTE: Objective Phase Iteration Value 2 1 10.000000 NOTE: Optimal. NOTE: Objective = 10.

The solution summary and primal solution are displayed in Output 8.4.4.

Output 8.4.4: Infeasibility Removed: Solution

Solution Summary Solver Dual Simplex Objective Function obj Solution Status Optimal Objective Value 10 Iterations 1     Primal Infeasibility 0 Dual Infeasibility 0 Bound Infeasibility 0 [1] x 1 0 2 10 3 0