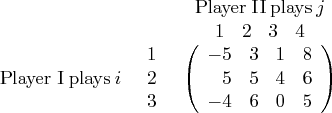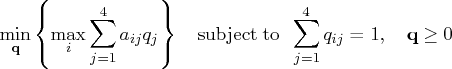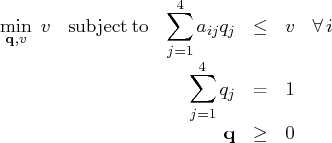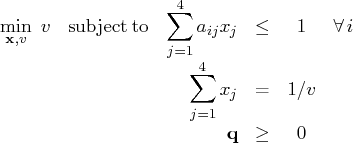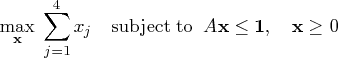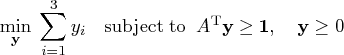The Linear Programming Solver: Example 8.3: Two-Person Zero-Sum Game :: SAS/OR(R) 9.2 User's Guide: Mathematical Programming

The Linear Programming Solver

Example 8.3: Two-Person Zero-Sum Game

Consider a two-person zero-sum game (where one person wins what the other person loses). The players make moves simultaneously, and each has a choice of actions. There is a payoff matrix that indicates the amount one player gives to the other under each combination of actions:

$& & {\rm player ii plays}\, j \ & &1 & 2 & 3 & 4 \ {\rm player i plays}\, i &1\2\3&( -5 & 3 & 1 & 8\ 5 & 5 & 4 & 6 \ -4 & 6 & 0 & 5 )$

If player I makes move and player II makes move , then player I wins (and player II loses) $a_{ij}$ . What is the best strategy for the two players to adopt? This example is simple enough to be analyzed from observation. Suppose player I plays 1 or 3; the best response of player II is to play 1. In both cases, player I loses and player II wins. So the best action for player I is to play 2. In this case, the best response for player II is to play 3, which minimizes the loss. In this case, (2, 3) is a pure-strategy Nash equilibrium in this game.

For illustration, consider the following mixed strategy case. Assume that player I selects with probability $p_i,\, i = 1, 2, 3$ , and player II selects with probability $q_j,\, j = 1, 2, 3, 4$ . Consider player II's problem of minimizing the maximum expected payout:

$\displaystyle\mathop{\min}_{\mathbf{q}}\{ \displaystyle\mathop{\max}_{i} \sum_{j... ...ij}q_j \} {\rm subject to} \;\; \sum_{j = 1}^4 q_{ij} = 1, \mathbf{q} \geq 0$

This is equivalent to

$\displaystyle\mathop{\min}_{\mathbf{q}, v}\; v & {\rm subject to} & \displaystyl... ...displaystyle\mathop\sum_{j=1}^4 q_j & = & 1 & \ & & \mathbf{q} & \geq & 0 &$

We can transform the problem into a more standard format by making a simple change of variables: . The preceding LP formulation now becomes

$\displaystyle\mathop{\min}_{\mathbf{x}, v}\; v & {\rm subject to} & \displaystyl... ...splaystyle\mathop\sum_{j=1}^4 x_j & = & 1/v & \ & & \mathbf{q} & \geq & 0 &$

which is equivalent to

$\displaystyle\mathop{\max}_{\mathbf{x}}\; \sum_{j = 1}^4 x_j {\rm subject to} \;\; a\mathbf{x} \leq \mathbf{1}, \mathbf{x} \geq 0$

where

is the payoff matrix and $\mathbf{1}$ is a vector of 1's. It turns out that the corresponding optimization problem from player I's perspective can be obtained by solving the dual problem, which can be written as

$\displaystyle\mathop{\min}_{\mathbf{y}}\; \sum_{i = 1}^3 y_i {\rm subject to} \;\; a^{\rm t}\mathbf{y} \geq \mathbf{1}, \mathbf{y} \geq 0$

You can model the problem and solve it by using PROC OPTMODEL as follows:

    proc optmodel;
       num a{1..3, 1..4}=[-5 3 1 8
                           5 5 4 6
                          -4 6 0 5];
       var x{1..4} >= 0;
       max f = sum{i in 1..4}x[i];
       con c{i in 1..3}: sum{j in 1..4}a[i,j]*x[j] <= 1;
       solve with lp / solver = ps presolver = none printfreq = 1;
       print x;
       print c.dual;
    quit;

The optimal solution is displayed in Output 8.3.1.

Output 8.3.1: Optimal Solutions to the Two-Person Zero-Sum Game

The OPTMODEL Procedure

Solution Summary
Solver	Primal Simplex
Objective Function	f
Solution Status	Optimal
Objective Value	0.25
Iterations	1

Primal Infeasibility	0
Dual Infeasibility	0
Bound Infeasibility	0

[1]	x
1	0.00
2	0.00
3	0.25
4	0.00

[1]	c.DUAL
1	0.00
2	0.25
3	0.00

The optimal solution $\mathbf{x}^* = (0, 0, 0.25, 0)$ with an optimal value of 0.25. Therefore the optimal strategy for player II is $\mathbf{q}^* = \mathbf{x}^*/0.25 = (0, 0, 1, 0)$ . You can check the optimal solution of the dual problem by using the constraint suffix ".dual". So $\mathbf{y}^* = (0, 0.25, 0)$ and player I's optimal strategy is (0, 1, 0). The solution is consistent with our intuition from observation.

Top of Page