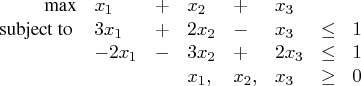The Linear Programming Solver

Getting Started

The following example illustrates how you can use the OPTMODEL procedure to solve linear programs. Suppose you want to solve the following problem:

${max} & x_1 & + & x_2 & + & x_3 & & \ { subject to } & 3 x_1 & + & 2x_2 & - & x... ...2x_1 & - & 3 x_2 & + & 2x_3 & \leq & 1 \ & & & x_1, & x_2, & x_3 & \geq & 0 \$

You can use the following statement to call the OPTMODEL procedure for solving linear programs:

    proc optmodel;
      var x{i in 1..3} >= 0;
 
      max f = x[1] + x[2] + x[3] ;
 
      con c1: 3*x[1] + 2*x[2]  - x[3]       <= 1;
      con c2: -2*x[1]  - 3*x[2]  +  2*x[3]  <= 1;
 
      solve with lp / solver = ps presolver = none printfreq = 1;
      print x;
    quit;

The optimal solution and the optimal objective value are displayed in Figure 8.1.

The OPTMODEL Procedure

Problem Summary
Objective Sense	Maximization
Objective Function	f
Objective Type	Linear

Number of Variables	3
Bounded Above	0
Bounded Below	3
Bounded Below and Above	0
Free	0
Fixed	0

Number of Constraints	2
Linear LE (<=)	2
Linear EQ (=)	0
Linear GE (>=)	0
Linear Range	0

The OPTMODEL Procedure

Solution Summary
Solver	Primal Simplex
Objective Function	f
Solution Status	Optimal
Objective Value	8
Iterations	2

Primal Infeasibility	0
Dual Infeasibility	0
Bound Infeasibility	0

[1]	x
1	0
2	3
3	5

Figure 8.1: Solution Summary

The iteration log displaying problem statistics, progress of the solution, and the optimal objective value is shown in Output 8.2.


NOTE: The problem has 3 variables (0 free, 0 fixed).
NOTE: The problem has 2 linear constraints (2 LE, 0 EQ, 0 GE, 0 range).
NOTE: The problem has 6 linear constraint coefficients.
NOTE: The problem has 0 nonlinear constraints (0 LE, 0 EQ, 0 GE, 0 range).
NOTE: The OPTLP presolver value NONE is applied.
NOTE: The PRIMAL SIMPLEX solver is called.
NOTE: Objective Entering Leaving
Phase Iteration Value Variable Variable
2 1 0.500000 x[3] c2 (S)
2 2 8.000000 x[2] c1 (S)
NOTE: Optimal.
NOTE: Objective = 8.

Figure 8.2: Log

Top of Page