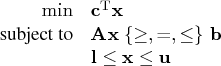The Linear Programming Solver

Overview

The OPTMODEL procedure provides a framework for specifying and solving linear programs (LPs). A standard linear program has the following formulation:

$\displaystyle\mathop{\min} & \mathbf{c}^{\rm t} \mathbf{x} \ {subject to} & \m... ...x}\;\{\ge, =, \le\}\; \mathbf{b} \ & \mathbf{l} \le \mathbf{x} \le \mathbf{u}$

where

$\mathbf{x}$	$\in$	$\mathbb{r}^n$	is the vector of decision variables
$\mathbf{a}$	$\in$	$\mathbb{r}^{m x n}$	is the matrix of constraints
$\mathbf{c}$	$\in$	$\mathbb{r}^n$	is the vector of objective function coefficients
$\mathbf{b}$	$\in$	$\mathbb{r}^m$	is the vector of constraints right-hand sides (RHS)
$\mathbf{l}$	$\in$	$\mathbb{r}^n$	is the vector of lower bounds on variables
$\mathbf{u}$	$\in$	$\mathbb{r}^n$	is the vector of upper bounds on variables

The following LP solvers are available in the OPTMODEL procedure:

primal simplex solver
dual simplex solver
interior point solver (experimental)

The simplex solvers implement the two-phase simplex method. In phase I, the solver tries to find a feasible solution. If no feasible solution is found, the LP is infeasible; otherwise, the solver enters phase II to solve the original LP. The interior point solver implements a primal-dual predictor-corrector interior point algorithm. If any of the decision variables are constrained to be integer-valued, then the relaxed version of the problem is solved.

Top of Page