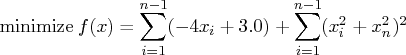Previous Page

|

Next Page

Example 7.2: Solving Unconstrained Optimization Problems

Although the IPNLP solver is suited for solving constrained NLP problems, it can solve efficiently unconstrained problems too. We demonstrate its ability by considering the following relatively large unconstrained NLP problem:

where . To solve this problem, you can write the following SAS code:

    proc optmodel;
       number N=5000;
       var x{1..N} init 1.0;
       
       minimize obj = sum {i in 1..N - 1} ( - 4 * x[i] + 3.0)  + 
                    sum {i in 1..N - 1} (x[i]^2 + x[N]^2)^2;
 
       solve with ipnlp;
    quit;
 

The problem and solution summaries are shown in Output 7.2.1.