PROC CLP: Constraint Data Set :: SAS/OR(R) 9.2 User's Guide: Constraint Programming

The CLP Procedure

The Constraint data set defines linear constraints, variable types, and bounds on variable domains. You can use a Constraint data set in lieu of, or in combination with, a LINCON and/or a VAR statement in order to define linear constraints, variable types, and variable bounds. The Constraint data set is similar to the problem data set input to the LP procedure in SAS/OR software and is specified using the CONDATA= option in the PROC CLP statement.

The Constraint data set must be in dense input format. In this format, a model’s columns appear as variables in the input data set and the data set must contain the _TYPE_ variable, the _RHS_ variable, and at least one numeric variable. In the absence of this requirement, the CLP procedure terminates. The _TYPE_ variable is a character variable that tells the CLP procedure how to interpret each observation. The CLP procedure recognizes the following keywords as valid values for the _TYPE_ variable: EQ, LE, GE, NE, LT, GT, LOWERBD, UPPERBD, BINARY, and FIXED. An optional character variable, _ID_, can be used to name each row in the Constraint data set.

Linear Constraints

For the _TYPE_ values EQ, LE, GE, NE, LT, GT, the corresponding observation is interpreted as a linear constraint. The _RHS_ variable is a numeric variable that contains the right-hand-side coefficient of the linear constraint. Any numeric variable other than _RHS_ that appears in a VAR statement is interpreted as a structural variable for the linear constraint.

EQ (=)

defines a linear equality

$\text{[math]}$

LE (<=)

defines a linear inequality of the form

$\text{[math]}$

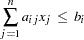
GE (>=)

defines a linear inequality of the form

$\text{[math]}$

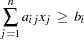
NE (<>)

defines a linear disequation of the form

$\text{[math]}$

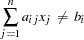
LT (<)

defines a linear inequality of the form

$\text{[math]}$

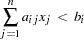
GT (>)

defines a linear inequality of the form

$\text{[math]}$

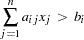
Domain Bounds

The values LOWERBD and UPPERBD specify additional lower bounds and upper bounds on the variable domains, respectively. In an observation where the _TYPE_ variable is equal to LOWERBD, a nonmissing value for a decision variable is considered a lower bound for that variable. Similarly, in an observation where the _TYPE_ variable is equal to UPPERBD, a nonmissing value for a decision variable is considered an upper bound for that variable. Note that lower and upper bounds as previously defined will be overridden by lower and upper bounds defined using a VAR statement.

Variable Types

The keywords BINARY and FIXED are interpreted as specifying numeric types. If the value of _TYPE_ is BINARY for an observation, then any decision variable with a nonmissing entry for the observation is interpreted as being a binary variable with domain {0,1}. If the value of _TYPE_ is FIXED for an observation, then any decision variable with a nonmissing entry for the observation is interpreted as being assigned to that nonmissing value. In other words, if the value of the variable X is $\text{[math]}$ in an observation for which _TYPE_ is FIXED, then the domain of X is considered to be the singleton { $\text{[math]}$ }. It is important to note that the value $\text{[math]}$ should belong to the domain of X, or the problem is deemed infeasible.

Variables in the CONDATA= Data Set

Table 1.2 lists all the variables associated with the Constraint data set and their interpretations by the CLP procedure. The table also lists for each variable its type (C for character, N for numeric), the possible values it can assume, and its default value.

Table 1.2 Constraint Data Set Variables
Name	Type	Description	Allowed Values	Default
_TYPE_	C	observation type	EQ, LE, GE, NE, LT, GT, LOWERBD, UPPERBD, BINARY, FIXED
_RHS_	N	right-hand-side coefficient		0
_ID_	C	observation name (optional)
Any numeric variable other than _RHS_	N	structural variable

Note: This procedure is experimental.

Top of Page