Time Series Analysis and Examples
Example 14.4 VAR Estimation and Variance Decomposition
In this example, a VAR(3) model is estimated and forecast. The data are investment, durable consumption, and consumption expenditures from Lütkepohl (1993). These data were previously analyzed in the section Minimum AIC Model Selection.
The stationary VAR(3) process is specified as
![\[ \mb{y}_ t = \bA _0 + \bA _1\mb{y}_{t-1} + \bA _2\mb{y}_{t-2} + \bA _3\mb{y}_{t-3} + \epsilon _ t \]](images/imlug_timeseriesexpls0452.png)
Output 14.4.1 shows that the matrix VARCOEF contains the AR coefficients (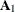 ,
,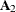 , and
, and 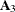 ). An intercept vector
). An intercept vector 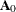 is included in the first row of the matrix VARCOEF if OPT[1]=1 is specified.
is included in the first row of the matrix VARCOEF if OPT[1]=1 is specified.
proc iml;
use var3;
read all var{invest income consum} into y;
close var3;
mdel = 1; maice = 0; misw = 0;
call tsmulmar(varCoef,ev,nar,aic) data=y maxlag=3
opt=(mdel || maice || misw) print=1;
print varCoef[c={"invest" "income" "consum"}];
Output 14.4.1: VAR Estimates
| varCoef | ||
|---|---|---|
| invest | income | consum |
| 4.8245814 | 5.3559216 | 17.066894 |
| 0.8855926 | 0.3401741 | -0.014398 |
| 0.1684523 | 1.0502619 | 0.107064 |
| 0.0891034 | 0.4591573 | 0.4473672 |
| -0.059195 | -0.298777 | 0.1629818 |
| 0.1128625 | -0.044039 | -0.088186 |
| 0.1684932 | -0.025847 | -0.025671 |
| 0.0637227 | -0.196504 | 0.0695746 |
| -0.226559 | 0.0532467 | -0.099808 |
| -0.303697 | -0.139022 | 0.2576405 |
To obtain the unit triangular matrix 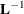 and diagonal matrix
and diagonal matrix 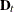 , you need to estimate the instantaneous response model. When you specify the OPT[3]=1 option, the first row of the output
matrix EV contains error variances of the instantaneous response model, while the unit triangular matrix is in the second
through fourth rows, as shown in Output 14.4.3.
, you need to estimate the instantaneous response model. When you specify the OPT[3]=1 option, the first row of the output
matrix EV contains error variances of the instantaneous response model, while the unit triangular matrix is in the second
through fourth rows, as shown in Output 14.4.3.
misw = 1; /*-- instantaneous model --*/
call tsmulmar(instCoef,ev,nar,aic) data=y maxlag=3
opt=(mdel || maice || misw) print=1;
print instCoef[c={"invest" "income" "consum"}], ev;
Output 14.4.2: Instantaneous Response Model Estimates
| instCoef | ||
|---|---|---|
| invest | income | consum |
| 4.8245814 | 5.2478984 | 13.147895 |
| 0.8855926 | 0.3401741 | -0.014398 |
| 0.1486237 | 1.0426454 | 0.1073864 |
| -0.222272 | -0.154018 | 0.3974399 |
| -0.059195 | -0.298777 | 0.1629818 |
| 0.1141878 | -0.037349 | -0.091835 |
| 0.1271453 | 0.0727963 | -0.023287 |
| 0.0637227 | -0.196504 | 0.0695746 |
| -0.227986 | 0.0576464 | -0.101366 |
| -0.20657 | -0.115316 | 0.2897901 |
Output 14.4.3: Error Variance and Unit Triangular Matrix
There is a relationship between the instantaneous response model and the VAR model. The VAR coefficients are computed as 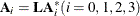 , where
, where 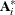 is a coefficient matrix of the instantaneous model. For example, you can verify this result by using the first lag coefficient
matrix
is a coefficient matrix of the instantaneous model. For example, you can verify this result by using the first lag coefficient
matrix 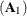 in Output 14.4.4.
in Output 14.4.4.
![\[ \left[\begin{array}{ccr} 0.886 & 0.340 & -0.014 \\ 0.168 & 1.050 & 0.107 \\ 0.089 & 0.459 & 0.447 \end{array}\right] = \left[\begin{array}{rcc} 1.000 & 0 & 0 \\ -0.022 & 1.000 & 0 \\ -0.256 & -0.501 & 1.000 \end{array}\right]^{-1} \left[\begin{array}{rrr} 0.886 & 0.340 & -0.014 \\ 0.149 & 1.043 & 0.107 \\ -0.222 & -0.154 & 0.397 \end{array}\right] \]](images/imlug_timeseriesexpls0462.png)
When the VAR estimates are available, you can forecast the future values by using the TSPRED call. As a default, the one-step
predictions are produced until the START= point is reached. The NPRED=h option specifies how far you want to predict. The prediction error covariance matrix MSE contains h mean square error matrices. The output matrix IMPULSE contains the estimate of the coefficients 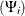 of the infinite MA process. The following SAS/IML statements estimate the VAR(3) model and perform a 10-step-ahead prediction.
Output 14.4.4 displays the first few rows of the matrix IMPULSE.
of the infinite MA process. The following SAS/IML statements estimate the VAR(3) model and perform a 10-step-ahead prediction.
Output 14.4.4 displays the first few rows of the matrix IMPULSE.
mdel = 1; maice = 0; misw = 0;
call tsmulmar(arcoef,ev,nar,aic) data=y maxlag=3
opt=(mdel || maice || misw);
call tspred(forecast,impulse,mse,y,arcoef,nar,0,ev)
npred=10 start=nrow(y) constant=mdel;
imp = impulse[1:12,]; /* 0,1,2,3 */
lag = colvec(char(T(0:3),1) || repeat(' ',4,2)); /* labels */
print imp[r=lag f=6.4];
Output 14.4.4: Moving-Average Coefficients: MA(0) MA(3)
MA(3)
The lagged effects of a unit increase in the error disturbances are included in the matrix IMPULSE. For example:
![\[ \frac{\partial \mb{y}_{t+2}}{\partial \epsilon ^{\prime }_ t} = \left[\begin{array}{ccc} 0.7811 & 0.3531 & 0.1802 \\ 0.4485 & 1.1655 & 0.0697 \\ 0.3646 & 0.6921 & 0.2223 \end{array}\right] \]](images/imlug_timeseriesexpls0465.png)
In addition, you can compute the lagged response on the one-unit increase in the orthogonalized disturbances 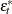 .
.
![\[ \frac{\partial \mb{y}_{t+m}}{\partial \epsilon _{jt}^*} = \frac{\partial \mr{E}(\mb{y}_{t+m}|y_{jt},y_{j-1,t},\ldots ,\bX _ t)}{\partial y_{jt}} = \Psi _ m \bL _ j \]](images/imlug_timeseriesexpls0298.png)
When the error matrix EV is obtained from the instantaneous response model, you need to convert the matrix IMPULSE. The first
few rows of the matrix ORTH_IMP are shown in Output 14.4.5. Note that the matrix constructed from the last three rows of EV become the matrix 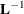 . The following statements compute the matrix ORTH_IMP:
. The following statements compute the matrix ORTH_IMP:
call tsmulmar(arcoef,ev,nar,aic) data=y maxlag=3 opt={1 0 1};
lmtx = inv(ev[2:nrow(ev),]);
orth_impulse = impulse * lmtx;
orth_imp = orth_impulse[1:12,];
print orth_imp[r=lag f=6.4];
Output 14.4.5: Transformed Moving-Average Coefficients
You can verify the result for the case of
![\[ \frac{\partial \mb{y}_{t+2}}{\partial \epsilon _{2t}^*} = \frac{\partial \mr{E}(\mb{y}_{t+2}|y_{2t},y_{1t},\ldots ,\bX _ t)}{\partial y_{2t}} = \Psi _2 \bL _2 \]](images/imlug_timeseriesexpls0466.png)
by using the simple computation
![\[ \left[\begin{array}{c} 0.4434 \\ 1.2004 \\ 0.8035 \end{array}\right] = \left[\begin{array}{ccc} 0.7811 & 0.3531 & 0.1802 \\ 0.4485 & 1.1655 & 0.0697 \\ 0.3646 & 0.6921 & 0.2223 \end{array}\right] \left[\begin{array}{c} 0.0000 \\ 1.0000 \\ 0.5008 \end{array}\right] \]](images/imlug_timeseriesexpls0467.png)
The contribution of the ith orthogonalized innovation to the mean square error matrix of the 10-step forecast is computed by using the formula
![\[ d_{ii}[\bL _ i \bL ^{\prime }_ i + \Psi _1 \bL _ i \bL ^{\prime }_ i \Psi ^{\prime }_1 + \cdots + \Psi _9 \bL _ i \bL ^{\prime }_ i \Psi ^{\prime }_9] \]](images/imlug_timeseriesexpls0468.png)
In Output 14.4.6, diagonal elements of each decomposed MSE matrix are displayed as the matrix CONTRIB as well as those of the MSE matrix (VAR). The following statements compute the matrices:
contrib = j(3,3);
do j = 1 to 3; /* for each variable */
mse_j = j(3,3,0); /* initial value for sum */
do i = 1 to 10; /* accumulate 10 steps */
/* accumulate matrix sum */
psi = impulse[(i-1)*3+1:3*i,];
mse_j = mse_j + psi*lmtx[,j]*lmtx[,j]`*psi`;
end;
mse_j = ev[1,j] # mse_j;
contrib[,j] = vecdiag(mse_j);
end;
var = vecdiag(mse[28:30,]);
print contrib var;
Output 14.4.6: Orthogonal Innovation Contribution
The investment innovation contribution to its own variable is 1879.3774, and the income innovation contribution to the consumption expenditure is 1916.1676. It is easy to understand the contribution of innovations in the ith variable to MSE when you compute the innovation account. In Output 14.4.7, innovations in the first variable (investment) explain 20.45% of the error variance of the second variable (income), while the innovations in the second variable explain 79.5% of its own error variance. It is straightforward to construct the general multistep forecast error variance decomposition, as follows:
account = 100 * contrib / var; print account;
Output 14.4.7: Innovation Account