Language Reference
NLPCG Call
CALL NLPCG (rc, xr, "fun", x0 <*>, opt <*>, blc <*>, tc <*>, par <*>, "ptit" <*>, "grd" );
The NLPCG subroutine uses the conjugate gradient method to solve a nonlinear optimization problem.
See the section Nonlinear Optimization and Related Subroutines for a listing of all NLP subroutines. See Chapter 15 for a description of the arguments of NLP subroutines.
The NLPCG subroutine requires function and gradient calls; it does not need second-order derivatives. The gradient vector
contains the first derivatives of the objective function f with respect to the parameters 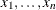 , as follows:
, as follows:
![\[ g(x) = \nabla f(x) = \left( \frac{\partial f}{\partial x_ j} \right) \]](images/imlug_langref0797.png)
If you do not specify a module with the "grd" argument, the first-order derivatives are approximated by finite difference formulas by using only function calls. The NLPCG algorithm can require many function and gradient calls, but it requires less memory than other subroutines for unconstrained optimization. In general, many iterations are needed to obtain a precise solution, but each iteration is computationally inexpensive. You can specify one of four update formulas for generating the conjugate directions with the fourth element of the opt input argument.
|
Value of opt[4] |
Update Method |
|---|---|
|
1 |
|
|
This is the default. |
|
|
2 |
Fletcher-Reeves update (Fletcher 1987) |
|
3 |
Polak-Ribiere update (Fletcher 1987) |
|
4 |
Conjugate-descent update of Fletcher (1987) |
The NLPCG subroutine is useful for optimization problems with large n. For the unconstrained or boundary-constrained case, the NLPCG method requires less memory than other optimization methods.
(The NLPCG method allocates memory proportional to n, whereas other methods allocate memory proportional to 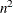 .) During n successive iterations, uninterrupted by restarts or changes in the working set, the conjugate gradient algorithm computes
a cycle of n conjugate search directions. In each iteration, a line search is done along the search direction to find an approximate optimum
of the objective function. The default line-search method uses quadratic interpolation and cubic extrapolation to obtain a
step size
.) During n successive iterations, uninterrupted by restarts or changes in the working set, the conjugate gradient algorithm computes
a cycle of n conjugate search directions. In each iteration, a line search is done along the search direction to find an approximate optimum
of the objective function. The default line-search method uses quadratic interpolation and cubic extrapolation to obtain a
step size  that satisfies the Goldstein conditions. One of the Goldstein conditions can be violated if the feasible region defines an
upper limit for the step size. You can specify other line-search algorithms with the fifth element of the opt argument.
that satisfies the Goldstein conditions. One of the Goldstein conditions can be violated if the feasible region defines an
upper limit for the step size. You can specify other line-search algorithms with the fifth element of the opt argument.
For an example of the NLPCG subroutine, see the section Constrained Betts Function.