Language Reference

Abramowitz, M., and Stegun, I. A., eds. (1972). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. 10th printing. New York: Dover.

Aiken, R. C. (1985). Stiff Computation. New York: Oxford University Press.

Al-Baali, M., and Fletcher, R. (1985). “Variational Methods for Nonlinear Least Squares.” Journal of the Operations Research Society 36:405–421.

Al-Baali, M., and Fletcher, R. (1986). “An Efficient Line Search for Nonlinear Least Squares.” Journal of Optimization Theory and Applications 48:359–377.

Ansley, C. F. (1979). “An Algorithm for the Exact Likelihood of a Mixed Autoregressive–Moving Average Process.” Biometrika 66:59–65.

Ansley, C. F. (1980). “Computation of the Theoretical Autocovariance Function for a Vector ARMA Process.” Journal of Statistical Computation and Simulation 12:15–24.

Ansley, C. F., and Kohn, R. (1986). “A Note on Reparameterizing a Vector Autoregressive Moving Average Model to Enforce Stationary.” Journal of Statistical Computation and Simulation 24:99–106.

Barnett, V., and Lewis, T. (1978). Outliers in Statistical Data. New York: John Wiley & Sons.

Barreto, H., and Maharry, D. (2006). “Least Median of Squares and Regression through the Origin.” Computational Statistics and Data Analysis 50:1391–1397.

Barrodale, I., and Roberts, F. D. K. (1974). “Algorithm 478: Solution of an Overdetermined System of Equations in the 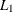-Norm.” Communications of the ACM 17:319–320.

Bates, D. M., Lindstrom, M. J., Wahba, G., and Yandell, B. S. (1987). “GCVPACK-Routines for Generalized Cross Validation.” Communications in Statistics—Simulation and Computation 16:263–297.

Beale, E. M. L. (1972). “A Derivation of Conjugate Gradients.” In Numerical Methods for Nonlinear Optimization, edited by F. A. Lootsma, 39–43. London: Academic Press.

Beaton, A. E. (1964). The Use of Special Matrix Operations in Statistical Calculus. Princeton, NJ: Educational Testing Service.

Bickart, T. A., and Picel, Z. (1973). “High Order Stiffly Stable Composite Multistep Methods for Numerical Integration of Stiff Differential Equations.” BIT 13:272–286.

Bishop, Y. M. M., Fienberg, S. E., and Holland, P. W. (1975). Discrete Multivariate Analysis: Theory and Practice. Cambridge, MA: MIT Press.

Box, G. E. P., and Jenkins, G. M. (1976). Time Series Analysis: Forecasting and Control. Rev. ed. San Francisco: Holden-Day.

Breiman, L. (1995). “Better Subset Regression Using the Nonnegative Garrote.” Technometrics 37:373–384.

Brent, R. P. (1973). Algorithms for Minimization without Derivatives. Englewood Cliffs, NJ: Prentice-Hall. Chapter 5.

Brewer, C. A. (2013). “ColorBrewer 2.0: Color Advice for Cartography.” Accessed June 4, 2013. http://colorbrewer.org/.

Brockwell, P. J., and Davis, R. A. (1991). Time Series: Theory and Methods. 2nd ed. New York: Springer-Verlag.

Brownlee, K. A. (1965). Statistical Theory and Methodology in Science and Engineering. New York: John Wiley & Sons.

Charnes, A., Frome, E. L., and Yu, P. L. (1976). “The Equivalence of Generalized Least Squares and Maximum Likelihood Estimation in the Exponential Family.” Journal of the American Statistical Association 71:169–171.

Christensen, R. (1997). Log-Linear Models and Logistic Regression. 2nd ed. New York: Springer-Verlag.

Chung, C. F. (1996). “A Generalized Fractionally Integrated ARMA Process.” Journal of Time Series Analysis 2:111–140.

Cox, D. R., and Hinkley, D. V. (1974). Theoretical Statistics. London: Chapman & Hall.

Daubechies, I. (1992). Ten Lectures on Wavelets. Vol. 61 of CBMS-NSF Regional Conference Series in Applied Mathematics. Philadelphia: Society for Industrial and Applied Mathematics.

Davies, L. (1992). “The Asymptotics of Rousseeuw’s Minimum Volume Ellipsoid Estimator.” Annals of Statistics 20:1828–1843.

De Boor, C. (1978). A Practical Guide to Splines. New York: Springer-Verlag.

De Jong, P. (1991). “Stable Algorithms for the State Space Model.” Journal of Time Series Analysis 12:143–157.

Dennis, J. E., Gay, D. M., and Welsch, R. E. (1981). “An Adaptive Nonlinear Least-Squares Algorithm.” ACM Transactions on Mathematical Software 7:348–368.

Dennis, J. E., and Mei, H. H. W. (1979). “Two New Unconstrained Optimization Algorithms Which Use Function and Gradient Values.” Journal of Optimization Theory and Applications 28:453–482.

Devroye, L. (1986). Non-uniform Random Variate Generation. New York: Springer-Verlag. http://luc.devroye.org/rnbookindex.html.

Donelson, J., and Hansen, E. (1971). “Cyclic Composite Predictor-Corrector Methods.” SIAM Journal on Numerical Analysis 8:137–157.

Donoho, D. L., and Johnstone, I. M. (1994). “Ideal Spatial Adaptation via Wavelet Shrinkage.” Biometrika 81:425–455.

Donoho, D. L., and Johnstone, I. M. (1995). “Adapting to Unknown Smoothness via Wavelet Shrinkage.” Journal of the American Statistical Association 90:1200–1224.

Duchon, J. (1976). “Fonctions-spline et espérances conditionnelles de champs gaussiens.” Annales scientifiques de l’Université de Clermont-Ferrand 2, Série Mathématique 14:19–27.

Emerson, P. L. (1968). “Numerical Construction of Orthogonal Polynomials from a General Recurrence Formula.” Biometrics 24:695–701.

Eskow, E., and Schnabel, R. B. (1991). “Algorithm 695: Software for a New Modified Cholesky Factorization.” ACM Transactions on Mathematical Software 17:306–312.

Fishman, G. S. (1996). Monte Carlo: Concepts, Algorithms, and Applications. New York: John Wiley & Sons.

Fletcher, R. (1987). Practical Methods of Optimization. 2nd ed. Chichester, UK: John Wiley & Sons.

Fletcher, R., and Xu, C. (1987). “Hybrid Methods for Nonlinear Least Squares.” Journal of Numerical Analysis 7:371–389.

Forsythe, G. E., Malcom, M. A., and Moler, C. B. (1967). Computer Solution of Linear Algebraic Systems. Chapter 17. Englewood Cliffs, NJ: Prentice-Hall.

Furnival, G. M., and Wilson, R. W. (1974). “Regression by Leaps and Bounds.” Technometrics 16:499–511.

Gaffney, P. W. (1984). “A Performance Evaluation of Some FORTRAN Subroutines for the Solution of Stiff Oscillatory Ordinary Differential Equations.” ACM Transactions on Mathematical Software 10:58–72.

Gay, D. M. (1983). “Subroutines for Unconstrained Minimization.” ACM Transactions on Mathematical Software 9:503–524.

Gentle, J. E. (2003). Random Number Generation and Monte Carlo Methods. 2nd ed. Berlin: Springer-Verlag.

Gentleman, W. M., and Sande, G. (1966). “Fast Fourier Transforms for Fun and Profit.” AFIPS Proceedings of the Fall Joint Computer Conference 19:563–578.

George, J. A., and Liu, J. W. (1981). Computer Solutions of Large Sparse Positive Definite Systems. Englewood Cliffs, NJ: Prentice-Hall.

Geweke, J., and Porter-Hudak, S. (1983). “The Estimation and Application of Long Memory Time Series Models.” Journal of Time Series Analysis 4:221–238.

Gill, P. E., Murray, W., Saunders, M. A., and Wright, M. H. (1984). “Procedures for Optimization Problems with a Mixture of Bounds and General Linear Constraints.” ACM Transactions on Mathematical Software 10:282–298.

Golub, G. H. (1969). “Matrix Decompositions and Statistical Calculations.” In Statistical Computation, edited by R. C. Milton, and J. A. Nelder, 365–397. New York: Academic Press.

Golub, G. H., and Van Loan, C. F. (1989). Matrix Computations. 2nd ed. Baltimore: Johns Hopkins University Press.

Gonin, R., and Money, A. H. (1989). Nonlinear 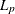-Norm Estimation. New York: Marcel Dekker.

Goodnight, J. H. (1979). “A Tutorial on the Sweep Operator.” American Statistician 33:149–158.

Graybill, F. A. (1969). Introduction to Matrices with Applications in Statistics. Belmont, CA: Wadsworth.

Grizzle, J. E., Starmer, C. F., and Koch, G. G. (1969). “Analysis of Categorical Data by Linear Models.” Biometrics 25:489–504.

Hadley, G. (1962). Linear Programming. Reading, MA: Addison-Wesley.

Harvey, A. C. (1989). Forecasting, Structural Time Series Models, and the Kalman Filter. Cambridge: Cambridge University Press.

Harville, D. A. (1997). Matrix Algebra from a Statistician’s Perspective. New York: Springer-Verlag.

Hocking, R. R. (1985). The Analysis of Linear Models. Monterey, CA: Brooks/Cole.

Jenkins, M. A., and Traub, J. F. (1970). “A Three-Stage Algorithm for Real Polynomials Using Quadratic Iteration.” SIAM Journal on Numerical Analysis 7:545–566.

Jennrich, R. I., and Moore, R. H. (1975). “Maximum Likelihood Estimation by Means of Nonlinear Least Squares.” American Statistical Association, 1975 Proceedings of the Statistical Computing Section 57–65.

Johnson, M. E. (1987). Multivariate Statistical Simulation. New York: John Wiley & Sons.

Kaiser, H. F., and Caffrey, J. (1965). “Alpha Factor Analysis.” Psychometrika 30:1–14.

Kastenbaum, M. A., and Lamphiear, D. E. (1959). “Calculation of Chi-Square to Test the No Three-Factor Interaction Hypothesis.” Biometrics 15:107–122.

Kohn, R., and Ansley, C. F. (1982). “A Note on Obtaining the Theoretical Autocovariances of an ARMA Process.” Journal of Statistical Computation and Simulation 15:273–283.

Korff, F. A., Taback, M. A. M., and Beard, J. H. (1952). “A Coordinated Investigation of a Food Poisoning Outbreak.” Public Health Reports 67:909–913.

Kotz, S., Balakrishnan, N., and Johnson, N. L. (2000). Continuous Multivariate Distributions. 2nd ed. New York: Wiley-Interscience.

Kotz, S., and Nadarajah, S. (2004). Multivariate t Distributions and Their Applications. Cambridge: Cambridge University Press.

Kruskal, J. B. (1964). “Multidimensional Scaling by Optimizing Goodness of Fit to a Nonmetric Hypothesis.” Psychometrika 29:1–27.

Lee, W., and Gentle, J. E. (1986). “The LAV Procedure.” In SUGI Supplemental Library User’s Guide, 257–260. Cary, NC: SAS Institute Inc.

Lewart, C. R. (1973). “Algorithm 463: Algorithms SCALE1, SCALE2, and SCALE3 for Determination of Scales on Computer Generated Plots.” Communications of the ACM 16:639–640. http://doi.acm.org/10.1145/362375.362417.

Lindström, P., and Wedin, P. A. (1984). “A New Line-Search Algorithm for Nonlinear Least-Squares Problems.” Mathematical Programming 29:268–296.

Madsen, K., and Nielsen, H. B. (1993). “A Finite Smoothing Algorithm for Linear 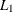Estimation.” SIAM Journal on Optimization 3:223–235.

Mallat, S. (1989). “Multiresolution Approximation and Wavelets.” Transactions of the American Mathematical Society 315:69–88.

Matsumoto, M., and Nishimura, T. (1998). “Mersenne Twister: A 623-Dimensionally Equidistributed Uniform Pseudo-random Number Generator.” ACM Transactions on Modeling and Computer Simulation 8:3–30.

Matsumoto, M., and Nishimura, T. (2002). “Mersenne Twister with Improved Initialization.” Accessed April 10, 2015. http://www.math.sci.hiroshima-u.ac.jp/~m-mat/MT/MT2002/emt19937ar.html.

McKean, J. W., and Schrader, R. M. (1987). “Least Absolute Errors Analysis of Variance.” In Statistical Data Analysis Based on 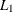Norm and Related Methods, edited by Y. Dodge, 297–305. Amsterdam: North-Holland.

McLeod, A. I. (1975). “Derivation of the Theoretical Autocovariance Function of Autoregressive–Moving Average Time Series.” Journal of the Royal Statistical Society, Series C 24:255–256.

Mittnik, S. (1990). “Computation of Theoretical Autocovariance Matrices of Multivariate Autoregressive Moving Average Time Series.” Journal of the Royal Statistical Society, Series B 52:151–155.

Moler, C. B. (2004). Numerical Computing with MATLAB. Natick, MA: MathWorks. http://www.mathworks.com/moler.

Moler, C. B. (2011). Experiments with MATLAB. Natick, MA: MathWorks. Available as e-book only. http://www.mathworks.com/moler/exm/chapters.html.

Monro, D. M., and Branch, J. L. (1977). “Algorithm AS 117: The Chirp Discrete Fourier Transform of General Length.” Journal of the Royal Statistical Society, Series C 26:351–361.

Moré, J. J. (1978). “The Levenberg-Marquardt Algorithm: Implementation and Theory.” In Lecture Notes in Mathematics, vol. 30, edited by G. A. Watson, 105–116. Berlin: Springer-Verlag.

Moré, J. J., and Sorensen, D. C. (1983). “Computing a Trust-Region Step.” SIAM Journal on Scientific and Statistical Computing 4:553–572.

Nelder, J. A., and Wedderburn, R. W. M. (1972). “Generalized Linear Models.” Journal of the Royal Statistical Society, Series A 135:370–384.

Nijenhuis, A., and Wilf, H. S. (1978). Combinatorial Algorithms. New York: Academic Press.

Nussbaumer, H. J. (1982). Fast Fourier Transform and Convolution Algorithms. 2nd ed. New York: Springer-Verlag.

Ogden, R. T. (1997). Essential Wavelets for Statistical Applications and Data Analysis. Boston: Birkhäuser.

Osborne, M. R. (1985). Finite Algorithms in Optimization and Data Analysis. New York: John Wiley & Sons.

Pizer, S. M. (1975). Numerical Computing and Mathematical Analysis. Chicago: Science Research Associates.

Pocock, S. J. (1977). “Group Sequential Methods in the Design and Analysis of Clinical Trials.” Biometrika 64:191–199.

Pocock, S. J. (1982). “Interim Analyses for Randomized Clinical Trials: The Group Sequential Approach.” Biometrics 38:153–162.

Powell, M. J. D. (1977). “Restart Procedures for the Conjugate Gradient Method.” Mathematical Programming 12:241–254.

Powell, M. J. D. (1978). “A Fast Algorithm for Nonlinearly Constrained Optimization Calculations.” In Lecture Notes in Mathematics, vol. 630, edited by G. A. Watson, 144–175. Berlin: Springer-Verlag.

Powell, M. J. D. (1982). VMCWD: A Fortran Subroutine for Constrained Optimization. Technical Report DAMTP 1982/NA4, Department of Applied Mathematics and Theoretical Physics, University of Cambridge.

Powell, M. J. D. (1992). A Direct Search Optimization Method That Models the Objective and Constraint Functions by Linear Interpolation. Technical Report DAMTP 1992/NA5, Department of Applied Mathematics and Theoretical Physics, University of Cambridge.

Ralston, A., and Rabinowitz, P. (1978). A First Course in Numerical Analysis. New York: McGraw-Hill.

Rao, C. R., and Mitra, S. K. (1971). Generalized Inverse of Matrices and Its Applications. New York: John Wiley & Sons.

Reinsch, C. H. (1967). “Smoothing by Spline Functions.” Numerische Mathematik 10:177–183.

Reinsel, G. C. (1997). Elements of Multivariate Time Series Analysis. 2nd ed. New York: Springer-Verlag.

Rice, S. O. (1973). “Efficient Evaluation of Integrals of Analytic Functions by the Trapezoidal Rule.” Bell System Technical Journal 52:707–722.

Rousseeuw, P. J. (1984). “Least Median of Squares Regression.” Journal of the American Statistical Association 79:871–880.

Rousseeuw, P. J. (1985). “Multivariate Estimation with High Breakdown Point.” In Mathematical Statistics and Applications, edited by W. Grossmann, G. Pflug, I. Vincze, and W. Wertz, 283–297. Dordrecht, Netherlands: D. Reidel Publishing.

Rousseeuw, P. J., and Croux, C. (1993). “Alternatives to the Median Absolute Deviation.” Journal of the American Statistical Association 88:1273–1283.

Rousseeuw, P. J., and Hubert, M. (1996). “Recent Development in PROGRESS.” Computational Statistics and Data Analysis 21:67–85.

Rousseeuw, P. J., and Hubert, M. (1997). “Recent Developments in PROGRESS.” 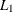-Statistical Procedures and Related Topics .

Rousseeuw, P. J., and Leroy, A. M. (1987). Robust Regression and Outlier Detection. New York: John Wiley & Sons.

Rousseeuw, P. J., and Van Driessen, K. (1998). Computing LTS Regression for Large Data Sets. Technical report, University of Antwerp.

Rousseeuw, P. J., and Van Driessen, K. (1999). “A Fast Algorithm for the Minimum Covariance Determinant Estimator.” Technometrics 41:212–223.

Rousseeuw, P. J., and Van Zomeren, B. C. (1990). “Unmasking Multivariate Outliers and Leverage Points.” Journal of the American Statistical Association 85:633–639.

Schatzoff, M., Tsao, R., and Fienberg, S. (1968). “Efficient Calculation of All Possible Regressions.” Technometrics 10:769–779.

Shampine, L. (1978). “Stability Properties of Adams Codes.” ACM Transactions on Mathematical Software 4:323–329.

Sikorsky, K. (1982). “Optimal Quadrature Algorithms in Spaces.” Numerische Mathematik 39:405–410.

Sikorsky, K., and Stenger, F. (1984). “Optimal Quadratures in Spaces.” ACM Transactions on Mathematical Software 3:140–151.

Singleton, R. C. (1969). “An Algorithm for Computing the Mixed Radix Fast Fourier Transform.” IEEE Transactions on Audio and Electroacoustics 17:93–103.

Sowell, F. (1992). “Maximum Likelihood Estimation of Stationary Univariate Fractionally Integrated Time Series Models.” Journal of Econometrics 53:165–188.

Squire, W. (1987). “Comparison of Gauss-Hermite and Midpoint Quadrature with Application to the Voigt Function.” In Numerical Integration: Recent Developments, edited by P. Keast, and G. Fairweather, 111–112. Dordrecht, Netherlands: D. Reidel Publishing.

Stenger, F. (1973a). “Integration Formulas Based on the Trapezoidal Formula.” Journal of the Institute of Mathematics and Its Applications 12:103–114.

Stenger, F. (1973b). “Remarks on Integration Formulas Based on the Trapezoidal Formula.” Journal of the Institute of Mathematics and Its Applications 19:145–147.

Stenger, F. (1978). “Optimal Convergence of Minimum Norm Approximations in .” Numerische Mathematik 29:345–362.

Stoer, J., and Bulirsch, R. (1980). Introduction to Numerical Analysis. New York: Springer-Verlag.

Thisted, R. A. (1988). Elements of Statistical Computing: Numerical Computation. London: Chapman & Hall.

Trotter, H. F. (1962). “Algorithm 115: PERM.” Communications of the ACM 5:434–435.

Wahba, G. (1990). Spline Models for Observational Data. Philadelphia: Society for Industrial and Applied Mathematics.

Wang, S. K., and Tsiatis, A. A. (1987). “Approximately Optimal One Parameter Boundaries for Group Sequential Trials.” Biometrics 43:193–199.

Wilkinson, J. H., and Reinsch, C. (1971). Handbook for Automatic Computation: Linear Algebra. Vol. 2. New York: Springer-Verlag.

Woodfield, T. J. (1988). “Simulating Stationary Gaussian ARMA Time Series.” In Computing Science and Statistics: Proceedings of the Twentieth Symposium on the Interface (Fairfax, VA), edited by E. J. Wegman, D. T. Gantz, and J. J. Miller, 612–617. Alexandria, VA: American Statistical Association.

Young, F. W. (1981). “Quantitative Analysis of Qualitative Data.” Psychometrika 46:357–388.