Nonlinear Optimization Examples
Constrained Betts Function
The linearly constrained Betts function (Hock and Schittkowski 1981) is defined as
![\[ f(x) = 0.01 x_1^2 + x_2^2 - 100 \]](images/imlug_nonlinearoptexpls0016.png)
The boundary constraints are
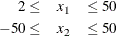
The linear constraint is
![\[ 10x_1 - x_2 \geq 10 \]](images/imlug_nonlinearoptexpls0018.png)
The following code calls the NLPCG subroutine to solve the optimization problem. The infeasible initial point 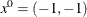 is specified, and a portion of the output is shown in Figure 15.3.
is specified, and a portion of the output is shown in Figure 15.3.
proc iml;
start F_BETTS(x);
f = .01 * x[1] * x[1] + x[2] * x[2] - 100.;
return(f);
finish F_BETTS;
con = { 2. -50. . .,
50. 50. . .,
10. -1. 1. 10.};
x = {-1. -1.};
optn = {0 2};
ods select ParameterEstimates LinCon ProblemDescription
IterStart IterHist IterStop LinConSol;
call nlpcg(rc,xres,"F_BETTS",x,optn,con);
quit;
The NLPCG subroutine performs conjugate gradient optimization. It requires only function and gradient calls. The F_BETTS module represents the Betts function, and since no module is defined to specify the gradient, first-order derivatives are computed by finite-difference approximations. For more information about the NLPCG subroutine, see the section NLPCG Call. For details about the constraint matrix, which is represented by the CON matrix in the preceding code, see the section Parameter Constraints.
Figure 15.3: NLPCG Solution to Betts Problem
Since the initial point 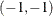 is infeasible, the subroutine first computes a feasible starting point. Convergence is achieved after three iterations, and
the optimal point is given to be
is infeasible, the subroutine first computes a feasible starting point. Convergence is achieved after three iterations, and
the optimal point is given to be 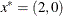 with an optimal function value of
with an optimal function value of 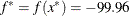 . For more information about the printed output, see the section Printing the Optimization History.
. For more information about the printed output, see the section Printing the Optimization History.