Language Reference
ARMACOV Call
CALL ARMACOV (auto, cross, convol, phi, theta, num);
The ARMACOV subroutine computes an autocovariance sequence for an autoregressive moving average (ARMA) model. The input arguments to the ARMACOV subroutine are as follows:
- phi
-
refers to a
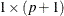 matrix that contains the autoregressive parameters. The first element is assumed to have the value 1.
matrix that contains the autoregressive parameters. The first element is assumed to have the value 1.
- theta
-
refers to a
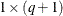 matrix that contains the moving average parameters. The first element is assumed to have the value 1.
matrix that contains the moving average parameters. The first element is assumed to have the value 1.
- num
-
refers to a scalar that contains n, the number of autocovariances to be computed, which must be a positive number.
The ARMACOV subroutine returns the following values:
- auto
-
specifies a variable to contain the returned
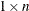 matrix that contains the autocovariances of the specified ARMA model, assuming unit variance for the innovation sequence.
matrix that contains the autocovariances of the specified ARMA model, assuming unit variance for the innovation sequence.
- cross
-
specifies a variable to contain the returned
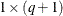 matrix that contains the covariances of the moving-average term with lagged values of the process.
matrix that contains the covariances of the moving-average term with lagged values of the process.
- convol
-
specifies a variable to contain the returned
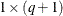 matrix that contains the autocovariance sequence of the moving-average term.
matrix that contains the autocovariance sequence of the moving-average term.
The ARMACOV subroutine computes the autocovariance sequence that corresponds to a given autoregressive moving-average (ARMA) time series model. An arbitrary number of terms in the sequence can be requested. Two related covariance sequences are also returned.
The model notation for the ARMACOV subroutine is the same as for the ARMALIK subroutine
. The ARMA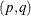 model is denoted
model is denoted
![\[ \sum _{j=0}^ p \phi _ j y_{t-j} = \sum _{i=0}^ q \theta _ i \epsilon _{t-i} \]](images/imlug_langref0061.png)
with 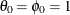 . The notation is the same as that of Box and Jenkins (1976) except that the model parameters are opposite in sign. The innovations
. The notation is the same as that of Box and Jenkins (1976) except that the model parameters are opposite in sign. The innovations 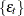 satisfy
satisfy 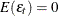 and
and 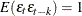 if k = 0, and are zero otherwise. The formula for the kth element of the convol argument is
if k = 0, and are zero otherwise. The formula for the kth element of the convol argument is
![\[ \sum _{i=k-1}^ q \theta _ i \theta _{i-k+1} \]](images/imlug_langref0066.png)
for 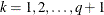 . The formula for the kth element of the cross argument is
. The formula for the kth element of the cross argument is
![\[ \sum _{i=k-1}^ q \theta _ i \psi _{i-k+1} \]](images/imlug_langref0068.png)
for 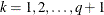 , where
, where 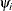 is the ith impulse response value. The
is the ith impulse response value. The 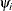 sequence, if desired, can be computed with the RATIO function
. It can be shown that
sequence, if desired, can be computed with the RATIO function
. It can be shown that 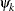 is the same as
is the same as 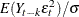 , which is used by Box and Jenkins (1976) in their formulation of the autocovariances. The kth autocovariance, denoted
, which is used by Box and Jenkins (1976) in their formulation of the autocovariances. The kth autocovariance, denoted 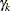 and returned as the
and returned as the 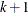 element of the auto argument
element of the auto argument 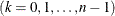 , is defined implicitly for
, is defined implicitly for 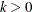 by
by
![\[ \sum _{i=0}^ p \gamma _{k-i} \phi _ i = \eta _ k \]](images/imlug_langref0076.png)
where 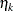 is the kth element of the cross argument. See Box and Jenkins (1976) or McLeod (1975) for more information.
is the kth element of the cross argument. See Box and Jenkins (1976) or McLeod (1975) for more information.
Consider the model
![\[ y_ t= 0.5y_{t-1} + e_ t + 0.8e_{t-1} \]](images/imlug_langref0078.png)
To compute the autocovariance function at lags zero through four for this model, use the following statements:
/* an ARMA(1,1) model */
phi = {1 -0.5};
theta = {1 0.8};
call armacov(auto, cross, convol, phi, theta, 5);
print auto, cross convol;
The result is show in Figure 25.46.
Figure 25.46: Result of the ARMACOV Subroutine