Language Reference
RATIO Function
RATIO (ar, ma, terms <, dim> );
The RATIO function divides matrix polynomials.
The arguments to the RATIO function are as follows:
- ar
-
is an
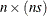 matrix that represents a matrix polynomial generating function,
matrix that represents a matrix polynomial generating function, 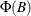 , in the variable B. The first
, in the variable B. The first 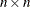 submatrix represents the constant term and must be nonsingular, the second
submatrix represents the constant term and must be nonsingular, the second 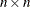 submatrix represents the first-order coefficients, and so on.
submatrix represents the first-order coefficients, and so on.
- ma
-
is an
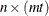 matrix that represents a matrix polynomial generating function,
matrix that represents a matrix polynomial generating function, 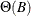 , in the variable B. The first
, in the variable B. The first 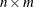 submatrix represents the constant term, the second
submatrix represents the constant term, the second 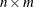 submatrix represents the first-order term, and so on.
submatrix represents the first-order term, and so on.
- terms
-
is a scalar that contains the number of terms to be computed, denoted by r in the following discussion. This value must be positive.
- dim
-
is a scalar that contains the value of m, a dimension of the matrix ma. The default value is 1.
The RATIO function multiplies a matrix of polynomials by the inverse of another matrix of polynomials. It is useful for expressing univariate and multivariate ARMA models in pure moving average or pure autoregressive forms.
The value returned is an 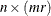 matrix that contains the terms of
matrix that contains the terms of 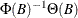 considered as a matrix of rational functions in B that have been expanded as power series.
considered as a matrix of rational functions in B that have been expanded as power series.
The RATIO function can be used to consolidate the matrix operators that are used in a multivariate time series model of the form
![\[ \Phi (B) \bY _ t = \Theta (B) \epsilon _ t \]](images/imlug_langref1173.png)
where 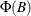 and
and 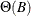 are matrix polynomial operators whose first matrix coefficients are identity matrices. The RATIO function can be used to
compute a truncated form of
are matrix polynomial operators whose first matrix coefficients are identity matrices. The RATIO function can be used to
compute a truncated form of 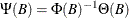 for the equivalent infinite-order model
for the equivalent infinite-order model
![\[ \bY _ t = \Psi (B) \epsilon _ t \]](images/imlug_langref1175.png)
The RATIO function can also be used for simple scalar polynomial division, giving a truncated form of 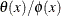 for two scalar polynomials
for two scalar polynomials 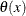 and
and 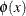 .
.
The cumulative sum of the elements of a column vector x can be obtained by using the following statement:
ratio({ 1 -1}, x, ncol(x));
The following example defines polynomial coefficients that are used in a multivariate ARMA(1,1) model and computes the ratio of the polynomials:
ar = {1 0 -0.5 2,
0 1 3 -0.8};
ma = {1 0 0.9 0.7,
0 1 2 -0.4};
psi = ratio(ar, ma, 4, 2);
print psi;
Figure 25.322: The Ratio of Polynomials