Wavelet Analysis
| Reconstructing the Signal from the Wavelet Decomposition |
You can use the WAVIFT subroutine to invert a wavelet transformation computed with the WAVFT subroutine. If no thresholding is specified, then up to numerical rounding error this inversion is exact. The following statements provide an illustration of this:
call wavift(reconstructedAbsorbance,decomp);
errorSS=ssq(absorbance-reconstructedAbsorbance);
print "The reconstruction error sum of squares = " errorSS;
The output is shown in Figure 19.15.
| errorSS | |
|---|---|
| The reconstruction error sum of squares = | 1.288E-16 |
Usually you use the WAVIFT subroutine with thresholding specified. This yields a smoothed reconstruction of the input data. You can use the following statements to create a smoothed reconstruction of absorbance and add this variable to the QuartzInfraredSpectrum data set.
call wavift(smoothedAbsorbance,decomp,&SureShrink);
create temp from smoothedAbsorbance[colname='smoothedAbsorbance'];
append from smoothedAbsorbance;
close temp;
quit;
data quartzInfraredSpectrum;
set quartzInfraredSpectrum;
set temp;
run;
The following statements produce the line plot of the smoothed absorbance data shown in Figure 19.16:
symbol1 c=black i=join v=none;
proc gplot data=quartzInfraredSpectrum;
plot smoothedAbsorbance*WaveNumber/
hminor = 0 vminor = 0
vaxis = axis1
hreverse frame;
axis1 label = ( r=0 a=90 );
run;
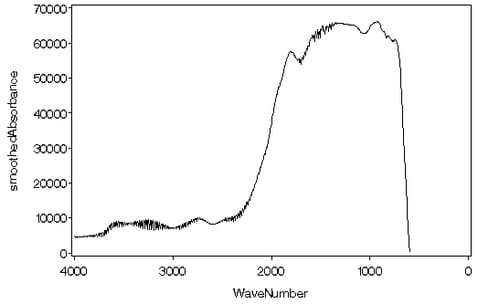
You can see by comparing Figure 19.1 with Figure 19.16 that the wavelet smooth of the absorbance data has preserved all the essential features of these data.
