| EIGEN Call |
The EIGEN subroutine computes eigenvalues and eigenvectors an arbitrary square numeric matrix.
The A argument is the input argument to the EIGEN subroutine. The EIGEN call returns the following values:
- evals
names a matrix to contain the eigenvalues of A.
- evecs
names a matrix to contain the right eigenvectors of A.
- vl
is an optional
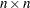matrix that contains the left eigenvectors of A in the same manner that evecs contains the right eigenvectors.
The EIGEN subroutine computes evals, a matrix that contains the eigenvalues of A. If A is symmetric, evals is the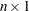 
vector that contains the 
real eigenvalues of A. If A is not symmetric (as determined by the criteria in the symmetry test described later), evals is an 
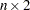matrix. The first column of evals contains the real parts, 
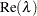, and the second column contains the imaginary parts, 
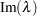. Each row represents one eigenvalue, 
.
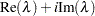If A is symmetric, the eigenvalues are arranged in descending order. Otherwise, the eigenvalues are sorted first by their real parts, then by the magnitude of their imaginary parts. Complex conjugate eigenvalues,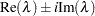 
, are stored in standard order; that is, the eigenvalue of the pair with a positive imaginary part is followed by the eigenvalue of the pair with the negative imaginary part.
The EIGEN subroutine also computes evecs, a matrix that contains the orthonormal column eigenvectors that correspond to evals. If A is symmetric, then the first column of evecs is the eigenvector that corresponds to the largest eigenvalue, and so forth. If A is not symmetric, then evecs is an 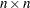matrix that contains the right eigenvectors of A. If the eigenvalue in row 
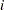of evals is real, then column 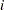of evecs contains the corresponding real eigenvector. If rows 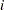and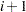 
of evals contain complex conjugate eigenvalues 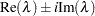, then columns 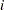and 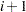of evecs contain the real part, 
, and imaginary part, 
, of the two corresponding eigenvectors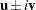 
.
The following paragraphs present some properties of eigenvalues and eigenvectors. Let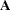 
be a general 
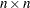matrix. The eigenvalues of 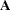are the roots of the characteristic polynomial, which is defined as 
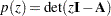. The spectrum, denoted by 
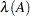, is the set of eigenvalues of the matrix 
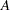. If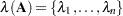 
, then 
.
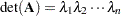The trace of 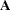is defined by
 |
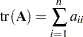and tr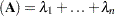
.
An eigenvector is a nonzero vector, 
, that satisfies 
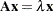for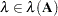 
. Right eigenvectors satisfy 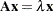, and left eigenvectors satisfy 
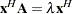, where 
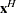is the complex conjugate transpose of 
. Taking the conjugate transpose of both sides shows that left eigenvectors also satisfy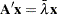 
.
The following are properties of the unsymmetric real eigenvalue problem, in which the real matrix 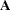is square but not necessarily symmetric:
The eigenvalues of an unsymmetric matrix
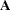can be complex. If 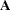has a complex eigenvalue, 
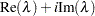, then the conjugate complex value 
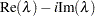is also an eigenvalue of 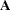. The right and left eigenvectors that correspond to a real eigenvalue of
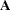are real. The right and left eigenvectors that correspond to conjugate complex eigenvalues of 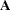are also conjugate complex. The left eigenvectors of
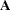are the same as the complex conjugate right eigenvectors of 
.
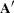The three routines, EIGEN, EIGVAL, and EIGVEC, use the following test of symmetry for a square argument matrix :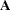
-
Select the entry of
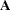with the largest magnitude: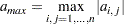 
Multiply the value of
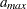by the square root of the machine precision, 
. The value of is the largest value stored in double precision that, when added to 1 in double precision, still results in 1. -
The matrix
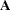is considered unsymmetric if there exists at least one pair of symmetric entries that differs in more than 
: 
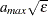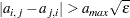
If 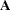is a symmetric matrix and 
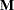and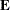 
are the eigenvalues and eigenvectors, respectively, of 
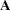, then the matrices have the following properties:
 |
 |
 |
|||
 |
|
 |
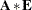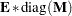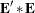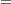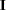These properties imply the following:
 |
 |
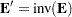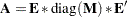The QL method is used to compute the eigenvalues (Wilkinson and Reinsch; 1971).
In statistical applications, nonsymmetric matrices for which eigenvalues are desired are usually of the form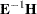 
, where 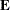and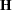 
are symmetric. The eigenvalues 
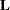and eigenvectors 
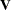of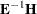 
can be obtained by using the GENEIG subroutine, or by using the following statements:
F = root(einv); A = F*H*F`; call eigen(L, W, A); V = F`*W;
The computation can be checked by forming the residuals, r, as shown in the following statement:
r = einv*H*V - V*diag(L);
The values in r should be of the order of rounding error.
The following statements compute the eigenvalues and left and right eigenvectors of a nonsymmetric matrix with four real and four complex eigenvalues:
A = {-1 2 0 0 0 0 0 0,
-2 -1 0 0 0 0 0 0,
0 0 0.2379 0.5145 0.1201 0.1275 0 0,
0 0 0.1943 0.4954 0.1230 0.1873 0 0,
0 0 0.1827 0.4955 0.1350 0.1868 0 0,
0 0 0.1084 0.4218 0.1045 0.3653 0 0,
0 0 0 0 0 0 2 2,
0 0 0 0 0 0 -2 0 };
call eigen(val, rvec, A) vecl="lvec";
print val;
The sorted eigenvalues of the A matrix are shown in Figure 23.100.
| val | |
|---|---|
| 1 | 1.7320508 |
| 1 | -1.732051 |
| 1 | 0 |
| 0.2087788 | 0 |
| 0.0222025 | 0 |
| 0.0026187 | 0 |
| -1 | 2 |
| -1 | -2 |
You can verify the correctness of the left and right eigenvector computation by using the following statements:
/* verify that the right eigenvectors are correct */
vec = rvec;
do j = 1 to ncol(vec);
/* if eigenvalue is real */
if val[j,2] = 0. then do;
v = A * vec[,j] - val[j,1] * vec[,j];
if any( abs(v) > 1e-12 ) then
badVectors = badVectors || j;
end;
/* if eigenvalue is complex with positive imaginary part */
else if val[j,2] > 0. then do;
/* the real part */
rp = val[j,1] * vec[,j] - val[j,2] * vec[,j+1];
v = A * vec[,j] - rp;
/* the imaginary part */
ip = val[j,1] * vec[,j+1] + val[j,2] * vec[,j];
u = A * vec[,j+1] - ip;
if any( abs(u) > 1e-12 ) | any( abs(v) > 1e-12 ) then
badVectors = badVectors || j || j+1;
end;
end;
if ncol( badVectors ) > 0 then
print "Incorrect right eigenvectors:" badVectors;
else print "All right eigenvectors are correct";
Similar statements can be written to verify the left eigenvectors. The statements use the fact that the left eigenvectors of 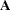are the same as the complex conjugate right eigenvectors of :
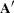/* verify that the left eigenvectors are correct */
vec = lvec;
do j = 1 to ncol(vec);
/* if eigenvalue is real */
if val[j,2] = 0. then do;
v = A` * vec[,j] - val[j,1] * vec[,j];
if any( abs(v) > 1e-12 ) then
badVectors = badVectors || j;
end;
/* if eigenvalue is complex with positive imaginary part */
else if val[j,2] > 0. then do;
/* Note the use of complex conjugation */
/* the real part */
rp = val[j,1] * vec[,j] + val[j,2] * vec[,j+1];
v = A` * vec[,j] - rp;
/* the imaginary part */
ip = val[j,1] * vec[,j+1] - val[j,2] * vec[,j];
u = A` * vec[,j+1] - ip;
if any( abs(u) > 1e-12 ) | any( abs(v) > 1e-12 ) then
badVectors = badVectors || j || j+1;
end;
end;
if ncol( badVectors ) > 0 then
print "Incorrect left eigenvectors:" badVectors;
else print "All left eigenvectors are correct";
The EIGEN call performs most of its computations in the memory allocated for returning the eigenvectors.