| GENEIG Call |
The GENEIG subroutine computes eigenvalues and eigenvectors of a generalized eigenproblem.
The input arguments to the GENEIG subroutine are as follows:
- sym-matrix1
is a symmetric numeric matrix.
- sym-matrix2
is a positive definite symmetric matrix.
The subroutine returns the following output arguments:
- evals
names a vector in which the eigenvalues are returned.
- evecs
names a matrix in which the corresponding eigenvectors are returned.
The GENEIG subroutine computes eigenvalues and eigenvectors of the generalized eigenproblem. If 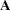 and
and 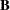 are symmetric and
are symmetric and 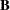 is positive definite, then the vector
is positive definite, then the vector 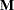 and the matrix
and the matrix 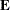 solve the generalized eigenproblem provided that
solve the generalized eigenproblem provided that
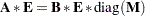 |
The vector 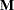 contains the eigenvalues arranged in descending order, and the matrix
contains the eigenvalues arranged in descending order, and the matrix 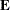 contains the corresponding eigenvectors in the columns.
contains the corresponding eigenvectors in the columns.
The following example is from Wilkinson and Reinsch (1971):
A = {10 2 3 1 1,
2 12 1 2 1,
3 1 11 1 -1,
1 2 1 9 1,
1 1 -1 1 15};
B = {12 1 -1 2 1,
1 14 1 -1 1,
-1 1 16 -1 1,
2 -1 -1 12 -1,
1 1 1 -1 11};
call geneig(M, E, A, B);
print M, E;
| M |
|---|
| 1.4923532 |
| 1.1092845 |
| 0.943859 |
| 0.6636627 |
| 0.4327872 |
| E | ||||
|---|---|---|---|---|
| -0.076387 | 0.142012 | 0.19171 | -0.08292 | -0.134591 |
| 0.017098 | 0.14242 | -0.158991 | -0.153148 | 0.0612947 |
| -0.066665 | 0.1209976 | 0.0748391 | 0.1186037 | 0.1579026 |
| 0.086048 | 0.125531 | -0.137469 | 0.182813 | -0.109466 |
| 0.2894334 | 0.0076922 | 0.0889779 | -0.003562 | 0.041473 |