| Robust Regression Examples |
Example 9.4: Brainlog Data
The following data, consisting of the body weights
(in kilograms) and brain weights (in grams) of 
animals, are reported by Jerison (1973) and can be
found also in Rousseeuw and Leroy (1987, p. 57).
Instead of the original data, the following example uses the
logarithms of the measurements of the two variables.
title "*** Brainlog Data: Do MCD, MVE ***";
aa={ 1.303338E-001 9.084851E-001 ,
2.6674530 2.6263400 ,
1.5602650 2.0773680 ,
1.4418520 2.0606980 ,
1.703332E-002 7.403627E-001 ,
4.0681860 1.6989700 ,
3.4060290 3.6630410 ,
2.2720740 2.6222140 ,
2.7168380 2.8162410 ,
1.0000000 2.0606980 ,
5.185139E-001 1.4082400 ,
2.7234560 2.8325090 ,
2.3159700 2.6085260 ,
1.7923920 3.1205740 ,
3.8230830 3.7567880 ,
3.9731280 1.8450980 ,
8.325089E-001 2.2528530 ,
1.5440680 1.7481880 ,
-9.208187E-001 .0000000 ,
-1.6382720 -3.979400E-001 ,
3.979400E-001 1.0827850 ,
1.7442930 2.2430380 ,
2.0000000 2.1959000 ,
1.7173380 2.6434530 ,
4.9395190 2.1889280 ,
-5.528420E-001 2.787536E-001 ,
-9.136401E-001 4.771213E-001 ,
2.2833010 2.2552720 };
By default, the MVE subroutine uses
only 1500 randomly selected subsets rather than all subsets.
The following specification of the options
vector requires that all 3276 subsets of 3 cases
out of 28 cases are generated and evaluated:
title2 "***MVE for BrainLog Data***";
title3 "*** Use All Subsets***";
optn = j(9,1,.);
optn[1]= 3; /* ipri */
optn[2]= 1; /* pcov: print COV */
optn[3]= 1; /* pcor: print CORR */
optn[5]= -1; /* nrep: all subsets */
call mve(sc,xmve,dist,optn,aa);
Specifying OPTN[1]=3, OPTN[2]=1, and OPTN[3]=1 requests that all output be printed. Output 9.4.1 shows the classical scatter and correlation matrix.
Output 9.4.1: Some Simple StatisticsOutput 9.4.2 shows the results of the combinatoric optimization (complete subset sampling).
Output 9.4.2: Iteration History for MVE|
|
| Subset | Singular | Best Criterion |
Percent |
| 819 | 0 | 0.439709 | 25 |
| 1638 | 0 | 0.439709 | 50 |
| 2457 | 0 | 0.439709 | 75 |
| 3276 | 0 | 0.439709 | 100 |
| Observations of Best Subset | ||
| 1 | 22 | 28 |
| Initial MVE Location Estimates |
|
| VAR1 | 1.3859759333 |
| VAR2 | 1.8022650333 |
| Initial MVE Scatter Matrix | ||
| VAR1 | VAR2 | |
| VAR1 | 4.9018525125 | 3.2937139101 |
| VAR2 | 3.2937139101 | 2.3400650932 |
Output 9.4.3 shows the optimization results after local improvement.
Output 9.4.3: Table of MVE Results|
|
| Robust MVE Location Estimates | |
| VAR1 | 1.29528238 |
| VAR2 | 1.8733722792 |
| Robust MVE Scatter Matrix | ||
| VAR1 | VAR2 | |
| VAR1 | 2.0566592937 | 1.5290250167 |
| VAR2 | 1.5290250167 | 1.2041353589 |
| Eigenvalues of Robust Scatter Matrix |
|
| VAR1 | 3.2177274012 |
| VAR2 | 0.0430672514 |
| Robust Correlation Matrix | ||
| VAR1 | VAR2 | |
| VAR1 | 1 | 0.9716184659 |
| VAR2 | 0.9716184659 | 1 |
Output 9.4.4 presents a table containing the classical Mahalanobis distances, the robust distances, and the weights identifying the outlier observations.
Output 9.4.4: Mahalanobis and Robust Distances|
|
| Classical Distances and Robust (Rousseeuw) Distances | |||
| Unsquared Mahalanobis Distance and | |||
| Unsquared Rousseeuw Distance of Each Observation | |||
| N | Mahalanobis Distances | Robust Distances | Weight |
| 1 | 1.006591 | 0.897076 | 1.000000 |
| 2 | 0.695261 | 1.405302 | 1.000000 |
| 3 | 0.300831 | 0.186726 | 1.000000 |
| 4 | 0.380817 | 0.318701 | 1.000000 |
| 5 | 1.146485 | 1.135697 | 1.000000 |
| 6 | 2.644176 | 8.828036 | 0 |
| 7 | 1.708334 | 1.699233 | 1.000000 |
| 8 | 0.706522 | 0.686680 | 1.000000 |
| 9 | 0.858404 | 1.084163 | 1.000000 |
| 10 | 0.798698 | 1.580835 | 1.000000 |
| 11 | 0.686485 | 0.693346 | 1.000000 |
| 12 | 0.874349 | 1.071492 | 1.000000 |
| 13 | 0.677791 | 0.717545 | 1.000000 |
| 14 | 1.721526 | 3.398698 | 0 |
| 15 | 1.761947 | 1.762703 | 1.000000 |
| 16 | 2.369473 | 7.999472 | 0 |
| 17 | 1.222253 | 2.805954 | 0 |
| 18 | 0.203178 | 1.207332 | 1.000000 |
| 19 | 1.855201 | 1.773317 | 1.000000 |
| 20 | 2.266268 | 2.074971 | 1.000000 |
| 21 | 0.831416 | 0.785954 | 1.000000 |
| 22 | 0.416158 | 0.342200 | 1.000000 |
| 23 | 0.264182 | 0.918383 | 1.000000 |
| 24 | 1.046120 | 1.782334 | 1.000000 |
| 25 | 2.911101 | 9.565443 | 0 |
| 26 | 1.586458 | 1.543748 | 1.000000 |
| 27 | 1.582124 | 1.808423 | 1.000000 |
| 28 | 0.394664 | 1.523235 | 1.000000 |
Again, you can call the subroutine SCATMVE(), which is included in the sample library in the file robustmc.sas, to plot the classical and robust confidence ellipsoids, as follows:
optn = j(9,1,.); optn[5]= -1;
vnam = { "Log Body Wgt","Log Brain Wgt" };
filn = "brlmve";
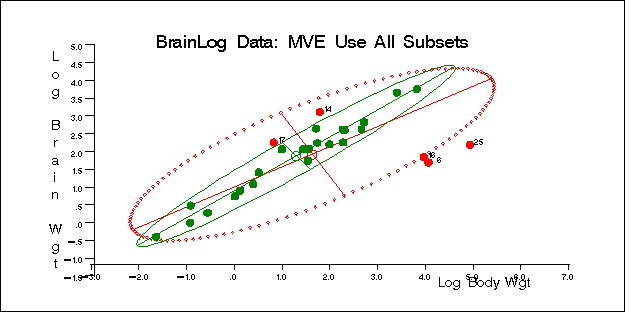
titl = "BrainLog Data: MVE Use All Subsets";
call scatmve(2,optn,.9,aa,vnam,titl,1,filn);
The plot is shown in Figure 9.4.5.
Output 9.4.5: BrainLog Data: Classical and Robust Ellipsoid(MVE)
|
MCD is another subroutine that can be used to compute the
robust location and the robust covariance of multivariate data sets.
Here is the code:
title2 "***MCD for BrainLog Data***";
title3 "*** Use 500 Random Subsets***";
optn = j(9,1,.);
optn[1]= 3; /* ipri */
optn[2]= 1; /* pcov: print COV */
optn[3]= 1; /* pcor: print CORR */
call mcd(sc,xmve,dist,optn,aa);
Similarly, specifying OPTN[1]=3, OPTN[2]=1, and OPTN[3]=1 requests that all output be printed.
Output 9.4.6 shows the results of the optimization.
Output 9.4.6: Results of the Optimization
| |||||||||||||||||||||||||||||||||
Output 9.4.7 shows the reweighted results after removing outliers.
Output 9.4.7: Final Reweighted MCD Results
| ||||||||||||||||||||||||||||||||||||
Output 9.4.8 presents a table containing the classical Mahalanobis distances, the robust distances, and the weights identifying the outlier observations.
Output 9.4.8: Mahalanobis and Robust Distances (MCD)
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
You can call the subroutine SCATMCD(), which is included in the sample library in file robustmc.sas, to plot the classical and robust confidence ellipsoids. Here is the code:
optn = j(9,1,.); optn[5]= -1;
vnam = { "Log Body Wgt","Log Brain Wgt" };
filn = "brlmcd";
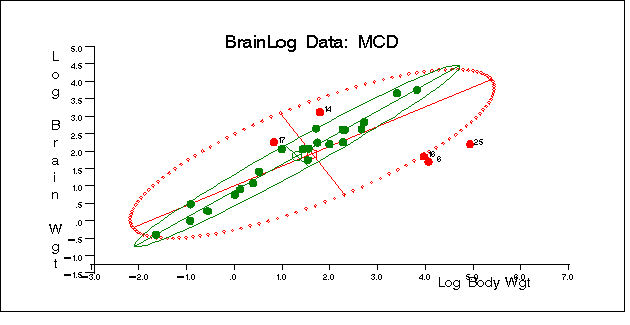
titl = "BrainLog Data: MCD";
call scatmcd(2,optn,.9,aa,vnam,titl,1,filn);
The plot is shown in Figure 9.4.9.
Output 9.4.9: BrainLog Data: Classical and Robust Ellipsoid (MCD)
|
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.