| Robust Regression Examples |
Example 9.2: Comparison of LMS, V7 LTS, and FAST-LTS
The following example presents comparisons of LMS, V7 LTS, and FAST-LTS.
The data analyzed are the stackloss data of Brownlee (1965), which are also
used for documenting the L1 regression module.
The three explanatory variables correspond to measurements for
a plant oxidizing ammonia to nitric acid on 21 consecutive days:
-
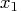 air flow to the plant
air flow to the plant
-
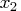 cooling water inlet temperature
cooling water inlet temperature
-
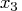 acid concentration
acid concentration
The response variable
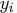
gives the
permillage of ammonia lost (stackloss).
The following data are also given in Rousseeuw and
Leroy (1987, p. 76) and Osborne (1985, p. 267):
print "Stackloss Data";
aa = { 1 80 27 89 42,
1 80 27 88 37,
1 75 25 90 37,
1 62 24 87 28,
1 62 22 87 18,
1 62 23 87 18,
1 62 24 93 19,
1 62 24 93 20,
1 58 23 87 15,
1 58 18 80 14,
1 58 18 89 14,
1 58 17 88 13,
1 58 18 82 11,
1 58 19 93 12,
1 50 18 89 8,
1 50 18 86 7,
1 50 19 72 8,
1 50 19 79 8,
1 50 20 80 9,
1 56 20 82 15,
1 70 20 91 15 };
Rousseeuw and Leroy (1987, p. 76) cite a large number
of papers in which the preceding data set was analyzed.
They state that most researchers ``concluded that
observations 1, 3, 4, and 21 were outliers'' and that
some people also reported observation 2 as an outlier.
Consider 2,000 Random Subsets for LMS
For
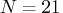
and
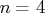
(three explanatory variables
including intercept), you obtain a total of 5985
different subsets of 4 observations out of 21.
If you do not specify OPTN[5], the LMS
algorithms draw
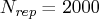
random sample subsets.
Since there is a large number of subsets with singular
linear systems that you do not want to print, you can
choose OPTN[2]=2 for reduced printed output, as in
the following:
title2 "***Use 2000 Random Subsets for LMS***";
a = aa[,2:4]; b = aa[,5];
optn = j(9,1,.);
optn[2]= 2; /* ipri */
optn[3]= 3; /* ilsq */
optn[8]= 3; /* icov */
call lms(sc,coef,wgt,optn,b,a);
Summary statistics are shown in Output 9.2.1.
Output 9.2.1: Some Simple Statistics
| Median
and Mean |
| |
Median |
Mean |
| VAR1 |
58 |
60.428571429 |
| VAR2 |
20 |
21.095238095 |
| VAR3 |
87 |
86.285714286 |
| Intercep |
1 |
1 |
| Response |
15 |
17.523809524 |
| Dispersion
and Standard Deviation |
| |
Dispersion |
StdDev |
| VAR1 |
5.930408874 |
9.1682682584 |
| VAR2 |
2.965204437 |
3.160771455 |
| VAR3 |
4.4478066555 |
5.3585712381 |
| Intercep |
0 |
0 |
| Response |
5.930408874 |
10.171622524 |
Output 9.2.2 displays the results of LS regression.
Output 9.2.2: Table of Unweighted LS Regression
| Unweighted
Least-Squares Estimation |
| LS
Parameter Estimates |
| Variable |
Estimate |
Approx
Std
Err |
t
Value |
Pr
> |t| |
Lower
WCI |
Upper
WCI |
| VAR1 |
0.7156402 |
0.13485819 |
5.31 |
<.0001 |
0.45132301 |
0.97995739 |
| VAR2 |
1.29528612 |
0.36802427 |
3.52 |
0.0026 |
0.57397182 |
2.01660043 |
| VAR3 |
-0.1521225 |
0.15629404 |
-0.97 |
0.3440 |
-0.4584532 |
0.15420818 |
| Intercep |
-39.919674 |
11.8959969 |
-3.36 |
0.0038 |
-63.2354 |
-16.603949 |
| Sum
of Squares = 178.8299616 |
| LS
Scale Estimate = 3.2433639182 |
| Cov
Matrix of Parameter Estimates |
| |
VAR1 |
VAR2 |
VAR3 |
Intercep |
| VAR1 |
0.0181867302 |
-0.036510675 |
-0.007143521 |
0.2875871057 |
| VAR2 |
-0.036510675 |
0.1354418598 |
0.0000104768 |
-0.651794369 |
| VAR3 |
-0.007143521 |
0.0000104768 |
0.024427828 |
-1.676320797 |
| Intercep |
0.2875871057 |
-0.651794369 |
-1.676320797 |
141.51474107 |
| F(3,17)
Statistic = 59.9022259 |
| Probability
= 3.0163272E-9 |
|
Output 9.2.3 displays the LMS results for the 2000 random subsets.
Output 9.2.3: Iteration History and Optimization Results
| Random Subsampling for LMS |
| Subset |
Singular |
Best
Criterion |
Percent |
| 500 |
23 |
0.163262 |
25 |
| 1000 |
55 |
0.140519 |
50 |
| 1500 |
79 |
0.140519 |
75 |
| 2000 |
103 |
0.126467 |
100 |
| Minimum Criterion= 0.1264668282 |
| Least Median of Squares (LMS) Method |
| Minimizing 13th Ordered Squared Residual. |
| Highest Possible Breakdown Value = 42.86 % |
| Random Selection of 2103 Subsets |
| Among 2103 subsets 103 are singular. |
| Observations of Best Subset |
| 15 |
11 |
19 |
10 |
| Estimated Coefficients |
| VAR1 |
VAR2 |
VAR3 |
Intercep |
| 0.75 |
0.5 |
0 |
-39.25 |
| LMS Objective Function = 0.75 |
| Preliminary LMS Scale = 1.0478510755 |
| Robust R Squared = 0.96484375 |
| Final LMS Scale = 1.2076147288 |
|
For LMS, observations 1, 3, 4, and 21 have
scaled residuals larger than 2.5 (output not
shown), and they are considered outliers.
Output 9.2.4 displays the corresponding WLS results.
Output 9.2.4: Table of Weighted LS Regression
| Weighted
Least-Squares Estimation |
| RLS
Parameter Estimates Based on LMS |
| Variable |
Estimate |
Approx
Std
Err |
t
Value |
Pr
> |t| |
Lower
WCI |
Upper
WCI |
| VAR1 |
0.79768556 |
0.06743906 |
11.83 |
<.0001 |
0.66550742 |
0.9298637 |
| VAR2 |
0.57734046 |
0.16596894 |
3.48 |
0.0041 |
0.25204731 |
0.9026336 |
| VAR3 |
-0.0670602 |
0.06160314 |
-1.09 |
0.2961 |
-0.1878001 |
0.05367975 |
| Intercep |
-37.652459 |
4.73205086 |
-7.96 |
<.0001 |
-46.927108 |
-28.37781 |
| Weighted
Sum of Squares = 20.400800254 |
| RLS
Scale Estimate = 1.2527139846 |
| Cov
Matrix of Parameter Estimates |
| |
VAR1 |
VAR2 |
VAR3 |
Intercep |
| VAR1 |
0.0045480273 |
-0.007921409 |
-0.001198689 |
0.0015681747 |
| VAR2 |
-0.007921409 |
0.0275456893 |
-0.00046339 |
-0.065017508 |
| VAR3 |
-0.001198689 |
-0.00046339 |
0.0037949466 |
-0.246102248 |
| Intercep |
0.0015681747 |
-0.065017508 |
-0.246102248 |
22.392305355 |
| Weighted
R-squared = 0.9750062263 |
| F(3,13)
Statistic = 169.04317954 |
| Probability
= 1.158521E-10 |
| There
are 17 points with nonzero weight. |
| Average
Weight = 0.8095238095 |
|
The subroutine PRILMTS(), which is in the
robustmc.sas file
that is contained in the sample library,
can be called to print the output summary. Here is
the statement:
call prilmts(3,sc,coef,wgt);
Output 9.2.5, Output 9.2.6, and Output 9.2.7 are the
three parts of the output.
Output 9.2.5: First Part of Output Generated by PRILMTS()
|
| Results of the Least Median Squares Estimation |
| Quantile: 13 |
| Number of Subsets: 2103 |
| Number of Singular Subsets: 103 |
| Number of Nonzero Weights: 17 |
| Objective Function: 0.75 |
| Preliminary Scale Estimate: 1.0478511 |
| Final Scale Estimate: 1.2076147 |
| Robust R-Squared: 0.9648438 |
| Asymptotic Consistency Factor: 1.1413664 |
| RLS Scale Estimate: 1.252714 |
| Weighted Sum of Squares: 20.4008 |
| Weighted R-Squared: 0.9750062 |
| F Statistic: 169.04318 |
|
Output 9.2.6: Second Part of Output Generated by PRILMTS()
Estimated
LMS Coefficients
0.75
0.5 0 -39.25
|
Indices
of Best Sample
15
11 19 10
|
Estimated
WLS Coefficients
0.7976856
0.5773405 -0.06706 -37.65246
|
Standard
Errors
0.0674391
0.1659689 0.0616031 4.7320509
|
T
Values
11.828242
3.4786054 -1.088584 -7.956901
|
Probabilities
2.4838E-8
0.004078 0.2961071 2.3723E-6
|
Lower
Wald CI
0.6655074
0.2520473 -0.1878 -46.92711
|
Upper
Wald CI
0.9298637
0.9026336 0.0536798 -28.37781
|
|
|
|
|
|
|
Output 9.2.7: Third Part of Output Generated by PRILMTS()
| LMS
Residuals |
|
6.4176097 2.2772163
6.21059 7.2456884
-0.20702 -0.621059 |
|
-0.20702
0.621059 -0.621059
0.621059
0.621059 0.2070197 |
|
-1.863177 -1.449138
0.621059 -0.20702
0.2070197 0.2070197 |
|
0.621059 1.863177
-6.831649 |
| Diagnostics |
|
10.448052 7.9317507
10 11.666667
2.7297297 3.4864865 |
|
4.7297297 4.2432432
3.6486486 3.7598351
4.6057675 4.9251688 |
|
3.8888889 4.5864209
5.2970297 4.009901
6.679576 4.3053404 |
|
4.0199755
3
11 |
| WLS
Residuals |
|
4.9634454 0.9185794
5.1312163 6.5250478 -0.535877
-0.996749 |
|
-0.338162 0.4601047 -0.844485
0.286883 0.7686702
0.377432 |
|
-2.000854 -1.074607
1.0731966 0.1143341
-0.297718 0.0770058 |
|
0.4679328 1.544008 -6.888934 |
|
Consider 2,000 Random Subsets for V7 LTS
The V7 LTS algorithm is similar to the LMS algorithm.
Here is the code:
title2 "***Use 2000 Random Subsets for LTS***";
a = aa[,2:4]; b = aa[,5];
optn = j(9,1,.);
optn[2]= 2; /* ipri */
optn[3]= 3; /* ilsq */
optn[8]= 3; /* icov */
optn[9]= 1; /* V7 LTS */
call lts(sc,coef,wgt,optn,b,a);
Output 9.2.8 displays the iteration history and optimization results
of V7 LTS.
Output 9.2.8: Iteration History and Optimization Results
| Random
Subsampling for LTS |
| Subset |
Singular |
Best
Criterion |
Percent |
| 500 |
23 |
0.099507 |
25 |
| 1000 |
55 |
0.087814 |
50 |
| 1500 |
79 |
0.084061 |
75 |
| 2000 |
103 |
0.084061 |
100 |
| Minimum
Criterion= 0.0840614072 |
| Least
Trimmed Squares (LTS) Method |
| Minimizing
Sum of 13 Smallest Squared Residuals. |
| Highest
Possible Breakdown Value = 42.86 % |
| Random
Selection of 2103 Subsets |
| Among
2103 subsets 103 are singular. |
| Observations
of Best Subset |
| 10 |
11 |
7 |
15 |
| Estimated
Coefficients |
| VAR1 |
VAR2 |
VAR3 |
Intercep |
| 0.75 |
0.3333333333 |
0 |
-35.70512821 |
| LTS
Objective Function = 0.4985185153 |
| Preliminary
LTS Scale = 1.0379336739 |
| Robust
R Squared = 0.9719626168 |
| Final
LTS Scale = 1.0407755737 |
|
In addition to observations 1, 3, 4, and 21, which
were considered outliers in LMS, observations 2 and 13 for
LTS have absolute scaled residuals that are larger
(but not as significantly as observations 1, 3, 4, and 21)
than 2.5 (output not shown).
Therefore, the WLS results based on LTS
are different from those based on LMS.
Output 9.2.9 displays the results for the weighted LS regression.
Output 9.2.9: Table of Weighted LS Regression
| Weighted Least-Squares Estimation |
| RLS Paramet
er Estimates Based on LTS |
| Variable |
Estimate |
Approx
Std Err |
t Value |
Pr > |t| |
Lower WCI |
Upper WCI |
| VAR1 |
0.75694055 |
0.07860766 |
9.63 |
<.0001 |
0.60287236 |
0.91100874 |
| VAR2 |
0.45353029 |
0.13605033 |
3.33 |
0.0067 |
0.18687654 |
0.72018405 |
| VAR3 |
-0.05211 |
0.05463722 |
-0.95 |
0.3607 |
-0.159197 |
0.054977 |
| Intercep |
-34.05751 |
3.82881873 |
-8.90 |
<.0001 |
-41.561857 |
-26.553163 |
| Weighted Sum of Squares = 10.273044977 |
| RLS Scale Estimate = 0.9663918355 |
| Cov Matrix of Parameter Estimates |
| |
VAR1 |
VAR2 |
VAR3 |
Intercep |
| VAR1 |
0.0061791648 |
-0.005776855 |
-0.002300587 |
-0.034290068 |
| VAR2 |
-0.005776855 |
0.0185096933 |
0.0002582502 |
-0.069740883 |
| VAR3 |
-0.002300587 |
0.0002582502 |
0.0029852254 |
-0.131487406 |
| Intercep |
-0.034290068 |
-0.069740883 |
-0.131487406 |
14.659852903 |
| Weighted R-squared = 0.9622869127 |
| F(3,11) Statistic = 93.558645037 |
| Probability = 4.1136826E-8 |
| There are 15 points with nonzero weight. |
| Average Weight = 0.7142857143 |
|
Consider 500 Random Subsets for FAST-LTS
The FAST-LTS algorithm uses only 500 random subsets
and gets better optimization results. Here is the code:
title2 "***Use 500 Random Subsets for FAST-LTS***";
a = aa[,2:4]; b = aa[,5];
optn = j(9,1,.);
optn[2]= 2; /* ipri */
optn[3]= 3; /* ilsq */
optn[8]= 3; /* icov */
optn[9]= 0; /* FAST-LTS */
call lts(sc,coef,wgt,optn,b,a);
For this example, the two LTS algorithms identify the same
outliers; however, the FAST-LTS algorithm uses only 500
random subsets and gets a smaller objective function,
as seen in Output 9.2.10. For
large data sets, the advantages of the FAST-LTS algorithm
are more obvious.
Output 9.2.10: Optimization Results for FAST-LTS
| LTS: The sum of the 13 smallest squared residuals will be minimized. |
| Unweighted Least-Squares Estimation |
| Sum of Squares = 178.8299616 |
| LS Scale Estimate = 3.2433639182 |
| F(3,17) Statistic = 59.9022259 |
| Probability = 3.0163272E-9 |
| Distribution of Residuals |
| Least Trimmed Squares (LTS) Method |
| Least Trimmed Squares (LTS) Method |
| Minimizing Sum of 13 Smallest Squared Residuals. |
| Highest Possible Breakdown Value = 42.86 % |
| Random Selection of 517 Subsets |
| Among 517 subsets 17 is/are singular. |
| The best half of the entire data set obtained after full iteration consists of the cases: |
| 5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
15 |
16 |
17 |
18 |
19 |
| Estimated Coefficients |
| VAR1 |
VAR2 |
VAR3 |
Intercep |
| 0.7409210642 |
0.3915267228 |
0.0111345398 |
-37.32332647 |
| LTS Objective Function = 0.474940583 |
| Preliminary LTS Scale = 0.9888435617 |
| Robust R Squared = 0.9745520119 |
| Final LTS Scale = 1.0360272594 |
| Distribution of Residuals |
| Weighted Least-Squares Estimation |
| Weighted Sum of Squares = 10.273044977 |
| RLS Scale Estimate = 0.9663918355 |
| Weighted R-squared = 0.9622869127 |
| F(3,11) Statistic = 93.558645037 |
| Probability = 4.1136826E-8 |
| There are 15 points with nonzero weight. |
| Average Weight = 0.7142857143 |
| Distribution of Residuals |
| The run has been executed successfully. |
|
Consider All 5,985 Subsets
You now report the results of LMS for all different subsets.
Here is the code:
title2 "*** Use All 5985 Subsets***";
a = aa[,2:4]; b = aa[,5];
optn = j(9,1,.);
optn[2]= 2; /* ipri */
optn[3]= 3; /* ilsq */
optn[5]= -1; /* nrep: all 5985 subsets */
optn[8]= 3; /* icov */
call lms(sc,coef,wgt,optn,b,a);
Output 9.2.11 displays the results for LMS.
Output 9.2.11: Iteration History and Optimization Results for LMS
| Complete Enumeration for LMS |
| Subset |
Singular |
Best
Criterion |
Percent |
| 1497 |
36 |
0.185899 |
25 |
| 2993 |
87 |
0.158268 |
50 |
| 4489 |
149 |
0.140519 |
75 |
| 5985 |
266 |
0.126467 |
100 |
| Minimum Criterion= 0.1264668282 |
| Least Median of Squares (LMS) Method |
| Minimizing 13th Ordered Squared Residual. |
| Highest Possible Breakdown Value = 42.86 % |
| Selection of All 5985 Subsets of 4 Cases Out of 21 |
| Among 5985 subsets 266 are singular. |
| Observations of Best Subset |
| 8 |
10 |
15 |
19 |
| Estimated Coefficients |
| VAR1 |
VAR2 |
VAR3 |
Intercep |
| 0.75 |
0.5 |
1.29526E-16 |
-39.25 |
| LMS Objective Function = 0.75 |
| Preliminary LMS Scale = 1.0478510755 |
| Robust R Squared = 0.96484375 |
| Final LMS Scale = 1.2076147288 |
|
Next, report the results of LTS for all different subsets, as follows:
title2 "*** Use All 5985 Subsets***";
a = aa[,2:4]; b = aa[,5];
optn = j(9,1,.);
optn[2]= 2; /* ipri */
optn[3]= 3; /* ilsq */
optn[5]= -1; /* nrep: all 5985 subsets */
optn[8]= 3; /* icov */
optn[9]= 1; /* V7 LTS */
call lts(sc,coef,wgt,optn,b,a);
Output 9.2.12 displays the results for LTS.
Output 9.2.12: Iteration History and Optimization Results for LTS
| Complete Enumeration for LTS |
| Subset |
Singular |
Best
Criterion |
Percent |
| 1497 |
36 |
0.135449 |
25 |
| 2993 |
87 |
0.107084 |
50 |
| 4489 |
149 |
0.081536 |
75 |
| 5985 |
266 |
0.081536 |
100 |
| Minimum Criterion= 0.0815355299 |
| Least Trimmed Squares (LTS) Method |
| Minimizing Sum of 13 Smallest Squared Residuals. |
| Highest Possible Breakdown Value = 42.86 % |
| Selection of All 5985 Subsets of 4 Cases Out of 21 |
| Among 5985 subsets 266 are singular. |
| Observations of Best Subset |
| 5 |
12 |
17 |
18 |
| Estimated Coefficients |
| VAR1 |
VAR2 |
VAR3 |
Intercep |
| 0.7291666667 |
0.4166666667 |
2.220446E-16 |
-36.22115385 |
| LTS Objective Function = 0.4835390299 |
| Preliminary LTS Scale = 1.0067458407 |
| Robust R Squared = 0.9736222371 |
| Final LTS Scale = 1.009470149 |
|
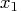 air flow to the plant
air flow to the plant
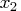 cooling water inlet temperature
cooling water inlet temperature
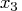 acid concentration
acid concentration