| Module Library |
RANDDIRICHLET Function
generates a random sample from a Dirichlet distribution
- RANDDIRICHLET( N, Shape )
The inputs are as follows:
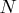
- is the number of desired observations sampled from the distribution.
- Shape
- is a
 vector of shape parameters for
the distribution,
vector of shape parameters for
the distribution, ![{shape}[i]\gt](images/modlib_modlibeq24.gif) .
.
The Dirichlet distribution is a multivariate generalization of the beta distribution. The RANDDIRICHLET function returns an
If
- the probability density function for
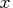 is
is
- if
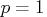 , the probability distribution is a beta distribution.
, the probability distribution is a beta distribution.
- if
 , then
, then
- the expected value of
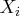 is
is  .
. - the variance of
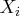 is
is  .
. - the covariance of
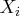 and
and 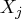 is
is  .
.
- the expected value of
The following example generates 1000 samples from a two-dimensional Dirichlet distribution. Each row of the returned matrix x is a row vector sampled from the Dirichlet distribution. The example then computes the sample mean and covariance and compares them with the expected values. Here are the code and the output:
call randseed(1);
n = 1000;
Shape = {2, 1, 1};
x = RANDDIRICHLET(n,Shape);
Shape0 = sum(Shape);
d = nrow(Shape)-1;
s = Shape[1:d];
ExpectedValue = s`/Shape0;
Cov = -s*s` / (Shape0##2*(Shape0+1));
/* replace diagonal elements with variance */
Variance = s#(Shape0-s) / (Shape0##2*(Shape0+1));
do i = 1 to d;
Cov[i,i] = Variance[i];
end;
SampleMean = x[:,];
n = nrow(x);
y = x - repeat( SampleMean, n );
SampleCov = y`*y / (n-1);
print SampleMean ExpectedValue, SampleCov Cov;
SampleMean ExpectedValue
0.4992449 0.2485677 0.5 0.25
SampleCov Cov
0.0502652 -0.026085 0.05 -0.025
-0.026085 0.0393922 -0.025 0.0375
For further details about sampling from the Dirichlet distribution, see Kotz, Balakrishnan, and Johnson (2000, p. 448); Gentle (2003, p. 205); or Devroye (1986, p. 593).
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.
