Language Reference

FFT Function

performs the finite Fourier transform

FFT( )

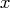where is a or numeric vector.

The FFT function returns the cosine and sine coefficients for the expansion of a vector into a sum of cosine and sine functions.

The argument of the FFT function, , is a or vector. The value returned is the resulting transform, an matrix, where

The elements of the first column of the returned matrix are the cosine coefficients; that is, the th element of the first column is

for , where the elements of are denoted as . The elements of the second column of the returned matrix are the sine coefficients; that is, the th element of the second column is

for .

Note: For most efficient use of the FFT function, should be a power of 2. If is a power of 2, a fast Fourier transform is used (Singleton 1969); otherwise, a Chirp-Z algorithm is used (Monro and Branch 1976).

The FFT function can be used to compute the periodogram of a time series. In conjunction with the inverse finite Fourier transform routine IFFT, the FFT function can be used to efficiently compute convolutions of large vectors (Gentleman and Sande 1966; Nussbaumer 1982).

As an example, suppose you measure a signal at constant time intervals. You believe the signal consists of a small number of Fourier components (that is, sines and cosines) corrupted by noise. The following code uses the FFT function to transform the signal into the frequency domain. The code then prints the frequencies with the largest amplitudes in the signal. According to this analysis, the signal is primarily composed of a constant signal, a signal with frequency 4 (for example, ), a signal with frequency one, and a signal with frequency 3. The amplitudes of the remaining Fourier components, are all substantially smaller.

  
    Signal = { 
     1.96  1.45  0.86  0.46  0.39  0.54 -1.65  0.60  0.43  0.20 
    -1.15  1.10  0.42  3.22  2.02  3.41  3.46  3.51  4.33  4.38 
     3.92  4.35  2.60  3.95  4.72  4.84  1.62  0.97  0.96  1.10 
     2.53  1.09  2.84  2.51  2.38  2.40  2.76  3.42  3.78  4.08 
     3.84  5.62  4.33  6.66  5.27  3.14  3.82  5.74  3.45  1.07 
     0.31  2.07  0.49 -1.85  0.61  0.35 -0.89 -0.92  0.33  2.31 
     1.13  2.28  3.73  3.78  2.63  4.15  5.27  3.62  5.99  3.79 
     4.00  3.18  3.03  3.52  2.08  1.70 -1.50 -1.35 -0.34 -1.52 
    -2.37 -2.84 -1.68 -2.22 -2.49 -3.28 -2.12 -0.81  0.84  1.91 
     2.10  2.24  1.24  3.24  2.89  3.14  4.21  2.65  4.67  3.87 
     }`; 
  
    z = fft(Signal); 
    Amplitude = z[,1]##2 + z[,2]##2; 
  
    /* find index into Amplitude so that idx[1] is the largest 
       value, idx[2] is the second largest value, etc. */ 
    call sortndx(idx,Amplitude,1,1); 
  
    /* print the 10 most dominant frequencies */ 
    Amplitude = Amplitude[idx[1:10],]; 
    print (idx[1:10]-1)[label="Freqs"] Amplitude[format=10.2]; 
  
  
                           Freqs  Amplitude 
  
                               0   38757.80 
                               4   13678.28 
                               1    4077.99 
                               3    2726.76 
                              26     324.23 
                              44     269.48 
                              12     224.09 
                              20     217.35 
                              11     202.30 
                              23     201.05
 

Based on these results, you might choose to filter the signal to keep only the most dominant Fourier components. One way to accomplish this is to eliminate any frequencies with small amplitudes. When the truncated frequencies are transformed back by using IFFT, you obtain a filtered version of the original signal. The following code performs these tasks:

  
    /* based on amplitudes, keep only first few dominant frequencies */ 
    NumFreqs = 4; 
    FreqsToDrop = idx[(NumFreqs+1):nrow(idx)]; 
    z[FreqsToDrop,] = 0; 
  
    FilteredSignal = ifft(z) / nrow(Signal);