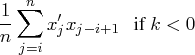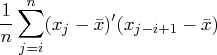Language Reference: COVLAG Function :: SAS/IML(R) 9.2 User's Guide

Language Reference

COVLAG Function

computes autocovariance estimates for a vector time series

COVLAG( , )

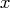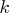The inputs to the COVLAG function are as follows:

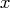
: is an 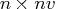matrix of time series values; 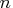is the number of observations, and 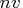is the dimension of the random vector.
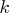
: is a scalar, the absolute value of which specifies the number of lags desired. If 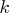is positive, a mean correction is made. If 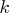is negative, no mean correction is made.

The COVLAG function computes a sequence of lagged crossproduct matrices. This function is useful for computing sample autocovariance sequences for scalar or vector time series.

The value returned by the COVLAG function is an

matrix. The

block of the matrix is the sum

$\frac{1}n \sum_{j=i}^n x_j^' x_{j-i+1} {if } k\lt$

where

is the

th row of

. If

> 0, then the

block of the matrix is

$\frac{1}n \sum_{j=i}^n (x_j-\bar{x})^'(x_{j-i+1}-\bar{x})$

where $\bar{x}$ is a row vector of the column means of

. For example, the following statements produce the matrix

, as shown:

  
    x={-9,-7,-5,-3,-1,1,3,5,7,9}; 
    cov=covlag(x,4);

  
               COV           1 row       4 cols    (numeric) 
  
                         33      23.1      13.6       4.9

Top of Page