Language Reference: CONVEXIT Function :: SAS/IML(R) 9.2 User's Guide

Language Reference

CONVEXIT Function

calculates and returns a scalar containing the convexity of a noncontingent cash flow

CONVEXIT( times,flows,ytm)

The CONVEXIT function calculates and returns a scalar containing the convexity of a noncontingent cash flow.

times: is an 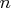-dimensional column vector of times. Elements should be nonnegative.
flows: is an 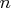-dimensional column vector of cash flows.
ytm: is the per-period yield-to-maturity of the cash-flow stream. This is a scalar and should be positive.

Convexity is essentially a measure of how duration, the sensitivity of price to yield, changes as interest rates change:

$c = \frac{1}p \frac{ d^2 p}{ dy^2 }$

With cash flows that are not yield sensitive, and the assumption of parallel shifts to a flat term structure, convexity is given by

$c= \frac{ \sum_{k=1}^k t_k (t_k+1) \frac{ c(k) } { (1+y)^{t_k} } } { p (1+y)^2 }$

where

is the present value,

is the effective per-period yield-to-maturity,

is the number of cash flows, and the

th cash flow is

periods from the present.

Consider the following statements:

  
    timesn=T(do(1,100,1)); 
    flows=repeat(10,100); 
    ytm=0.1; 
    convexit=convexit(timesn,flows,ytm); 
    print convexit;

These statements result in the following output:

  
    CONVEXIT 
    199.26229