| Language Reference |
BSPLINE Function
computes a B-spline basis
- BSPLINE(
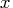 ,
, 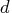 ,
, 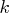
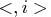 )
)
The inputs to the BSPLINE function are as follows:
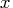
- is an
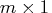 or
or 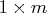 numeric vector.
numeric vector.
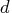
- is a nonnegative numeric scalar value that specifies the degree of the
B-spline. Note that the order of a B-spline is one greater than the
degree.
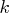
- is a numeric vector of size
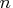 that contains the B-spline
knots or a scalar that denotes the number of interior knots.
When
that contains the B-spline
knots or a scalar that denotes the number of interior knots.
When 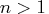 , the elements of the knot vector must be nondecreasing,
, the elements of the knot vector must be nondecreasing,
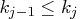 for
for 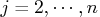 .
. 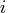
- is an optional argument that specifies the number of interior knots
when
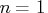 and
and 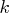 contains a missing value. In this case the
BSPLINE function constructs a vector of knots as follows. If
contains a missing value. In this case the
BSPLINE function constructs a vector of knots as follows. If 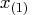 and
and 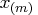 are the smallest and largest value in the
are the smallest and largest value in the 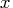 vector,
then interior knots are placed at
vector,
then interior knots are placed at
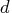 exterior knots are placed under
exterior knots are placed under 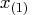 and
max(
and
max(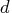 ,1) exterior knots are placed over
,1) exterior knots are placed over 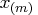 . The exterior
knots are evenly spaced and start at
. The exterior
knots are evenly spaced and start at 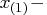 1E-12 and
1E-12 and 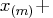 1E-12. In this case the BSPLINE function returns a matrix with
1E-12. In this case the BSPLINE function returns a matrix with 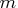 rows
and
rows
and 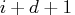 columns.
columns.
The BSPLINE function computes B-splines of degree
Note that de Boor (2001) expresses B-splines in terms of order rather
than degree; in his notation ![]() . B-splines have
many interesting properties. For example:
. B-splines have
many interesting properties. For example:
-
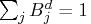
- The sequence
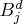 is positive on
is positive on 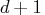 knots and zero
elsewhere.
knots and zero
elsewhere.
- The B-spline
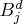 is a piecewise polynomial of at most
is a piecewise polynomial of at most
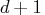 pieces.
pieces.
- If
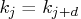 , then
, then 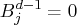 .
.
A typical knot vector for calculating B-splines consists of ![]() exterior knots smaller than the smallest data value, and
exterior knots smaller than the smallest data value, and ![]() exterior knots larger than the largest data value. The remaining knots
are the interior knots.
exterior knots larger than the largest data value. The remaining knots
are the interior knots.
For example, consider the following statements and the output they produce:
x = {2.5 3 4.5 5.1};
knots = {0 1 2 3 4 5 6 7 8};
bsp = bspline(x,3,knots);
print bsp[format=best7.];
0.02083 0.47917 0.47917 0.02083 0 0 0
0 0.16667 0.66667 0.16667 0 0 0
0 0 0.02083 0.47917 0.47917 0.02083 0
0 0 0 0.1215 0.65717 0.22117 0.00017
In this example there are
n = 20;
x = ranuni(J(n,1,45));
bsp = bspline(x,2,.,4);
print bsp[format=8.3];
The resulting matrix is as follows:
0.000 0.104 0.748 0.147 0.000 0.000 0.000
0.000 0.000 0.000 0.286 0.684 0.030 0.000
0.000 0.000 0.000 0.000 0.000 0.517 0.483
0.000 0.000 0.000 0.217 0.725 0.058 0.000
0.000 0.000 0.239 0.713 0.048 0.000 0.000
0.000 0.000 0.000 0.446 0.553 0.002 0.000
0.000 0.000 0.394 0.600 0.006 0.000 0.000
0.000 0.000 0.000 0.000 0.064 0.729 0.207
0.000 0.389 0.604 0.007 0.000 0.000 0.000
0.000 0.000 0.000 0.000 0.000 0.500 0.500
0.000 0.000 0.000 0.000 0.210 0.728 0.062
0.000 0.000 0.014 0.639 0.347 0.000 0.000
0.000 0.001 0.546 0.453 0.000 0.000 0.000
0.500 0.500 0.000 0.000 0.000 0.000 0.000
0.304 0.672 0.024 0.000 0.000 0.000 0.000
0.000 0.020 0.659 0.322 0.000 0.000 0.000
0.000 0.277 0.690 0.033 0.000 0.000 0.000
0.386 0.606 0.007 0.000 0.000 0.000 0.000
0.000 0.000 0.000 0.000 0.022 0.667 0.311
0.008 0.612 0.380 0.000 0.000 0.000 0.000
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.