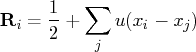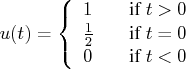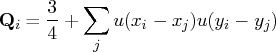Language Reference

BRANKS Function

computes bivariate ranks

BRANKS( matrix)

where matrix is an numeric matrix.

The BRANKS function calculates the tied ranks and the bivariate ranks for an matrix and returns an matrix of these ranks. The tied ranks of the first column of matrix are contained in the first column of the result matrix; the tied ranks of the second column of matrix are contained in the second column of the result matrix; and the bivariate ranks of matrix are contained in the third column of the result matrix.

The tied rank of an element of a vector is defined as

where

The bivariate rank of a pair is defined as

For example, consider the following statements and the output they produce:

  
    x={1 0, 
       4 2, 
       3 4, 
       5 3, 
       6 3}; 
    f=branks(x); 
  
               F             5 rows      3 cols    (numeric) 
  
                               1         1         1 
                               3         2         2 
                               2         5         2 
                               4       3.5         3 
                               5       3.5       3.5