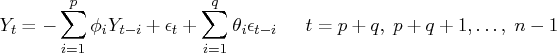Language Reference: ARMASIM Function :: SAS/IML(R) 9.2 User's Guide

Language Reference

ARMASIM Function

simulates a univariate ARMA series

ARMASIM( phi, theta, mu, sigma, 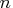, <seed>)

The inputs to the ARMASIM function are as follows:

phi: is a 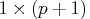matrix containing the autoregressive parameters. The first element is assumed to have the value 1.
theta: is a 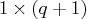matrix containing the moving-average parameters. The first element is assumed to have the value 1.
mu: is a scalar containing the overall mean of the series.
sigma: is a scalar containing the standard deviation of the innovation series.
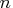
: is a scalar containing 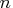, the length of the series. The value of 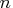must be greater than 0.
seed: is a scalar containing the random number seed. At the first execution of the function, the seed variable is used as follows:

If seed > 0, the input seed is used for generating the series.

If seed = 0, the system clock is used to generate the seed.

If seed < 0, the value (-1)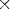(seed) is used for generating the series.

If the seed is not supplied, the system clock is used to generate the seed.

On subsequent calls of the function in the DO loop - like environment, the seed variable is used as follows: If seed > 0, the seed remains unchanged. In other cases, after each execution of the function, the current seed is updated internally.

The ARMASIM function generates a series of length

from a given autoregressive moving-average (ARMA) time series model and returns the series in an

matrix. The notational conventions for the ARMASIM function are the same as those used by the ARMACOV subroutine. See the description of the ARMACOV call for the model employed. The ARMASIM function uses an exact simulation algorithm as described in Woodfield (1988). A sequence $y_0,y_1, ... ,y_{p+q-1}$ of starting values is produced by using an expanded covariance matrix, and then the remaining values are generated by using the following recursion form of the model:

$y_t = -\sum_{i=1}^p \phi_i y_{t-i} + \epsilon_t + \sum_{i=1}^q \theta_i \epsilon_{t-i} t = p+q, p+q+1, ... , n-1$

The random number generator RANNOR is used to generate the noise component of the model. Note that the following statement returns

standard normal pseudo-random deviates:

armasim(1,1,0,1,n,seed);

For example, consider the following model:

$y_t= 0.5y_{t-1} + e_t + 0.8e_{t-1}$

To generate a time series of length 10 from this model, use the following code to produce the result shown:

  
    phi={1 -0.5}; 
    theta={1 0.8}; 
    y=armasim(phi, theta, 0, 1, 10, -1234321); 
    print y;

Top of Page