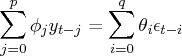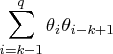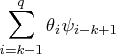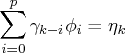Language Reference: ARMACOV Call :: SAS/IML(R) 9.2 User's Guide

Language Reference

ARMACOV Call

computes an autocovariance sequence for an ARMA model

CALL ARMACOV( auto, cross, convol, phi, theta, num);

The inputs to the ARMACOV subroutine are as follows:

phi: refers to a 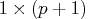matrix containing the autoregressive parameters. The first element is assumed to have the value 1.
theta: refers to a 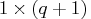matrix containing the moving-average parameters. The first element is assumed to have the value 1.
num: refers to a scalar containing 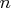, the number of autocovariances to be computed, which must be a positive number.

The ARMACOV subroutine returns the following values:

auto: specifies a variable to contain the returned 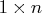matrix containing the autocovariances of the specified ARMA model, assuming unit variance for the innovation sequence.
cross: specifies a variable to contain the returned 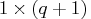matrix containing the covariances of the moving-average term with lagged values of the process.
convol: specifies a variable to contain the returned 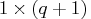matrix containing the autocovariance sequence of the moving-average term.

The ARMACOV subroutine computes the autocovariance sequence that corresponds to a given autoregressive moving-average (ARMA) time series model. An arbitrary number of terms in the sequence can be requested. Two related covariance sequences are also returned.

The model notation for the ARMACOV and ARMALIK subroutines is the same. The ARMA

model is denoted

$\sum_{j=0}^p \phi_j y_{t-j} = \sum_{i=0}^q \theta_i \epsilon_{t-i}$

with $\theta_0 = \phi_0 = 1$ . The notation is the same as that of Box and Jenkins (1976) except that the model parameters are opposite in sign. The innovations $\{\epsilon_t\}$ satisfy $e(\epsilon_t)=0$ and $e(\epsilon_t \epsilon_{t-k})=1$ if

= 0, and are zero otherwise. The formula for the

th element of the convol argument is

$\sum_{i=k-1}^q \theta_i \theta_{i-k+1}$

for

. The formula for the

th element of the cross argument is

$\sum_{i=k-1}^q \theta_i \psi_{i-k+1}$

for

, where $\psi_i$ is the

th impulse response value. The $\psi_i$ sequence, if desired, can be computed with the RATIO function. It can be shown that $\psi_k$ is the same as $e(y_{t-k} \epsilon^2_t)/\sigma$ , which is used by Box and Jenkins (1976, p. 75) in their formulation of the autocovariances. The

th autocovariance, denoted $\gamma_k$ and returned as the

element of the auto argument

, is defined implicitly for $k\gt$ by

$\sum_{i=0}^p \gamma_{k-i} \phi_i = \eta_k$

where $\eta_k$ is the

th element of the cross argument. See Box and Jenkins (1976) or McLeod (1975) for more information.

Consider the model

$y_t= 0.5y_{t-1} + e_t + 0.8e_{t-1}$

To compute the autocovariance function at lags zero through four for this model, use the following statements:

  
       /* an arma(1,1) model */ 
       phi  ={1 -0.5}; 
       theta={1 0.8}; 
       call armacov(auto,cross,convol,phi,theta,5); 
       print auto,,cross convol;

The result is as follows:

  
                AUTO 
           3.2533333 2.4266667 1.2133333 0.6066667 0.3033333 
  
  
                     CROSS              CONVOL 
                      2.04       0.8      1.64       0.8

Top of Page