Language Reference

WAVFT Call

computes fast wavelet transform

CALL WAVFT( decomp, data, opt <, levels> );

The fast wavelet transform (WAVFT) subroutine computes a specified discrete wavelet transform of the input data by using the algorithm of Mallat (1989). This transform decomposes the input data into sets of detail and scaling coefficients defined at a number of scales or "levels."

The input data are used as scaling coefficients at the top level in the decomposition. The fast wavelet transform then recursively computes a set of detail and a set of scaling coefficients at the next lower level by respectively applying "low pass" and "high pass" conjugate mirror filters to the scaling coefficients at the current level. The number of coefficients in each of these new sets is approximately half the number of scaling coefficients at the level above them. Depending on the filters being used, a number of additional scaling coefficients, known as boundary coefficients, can be involved. These boundary coefficients are obtained by extending the sequence of interior scaling coefficients using a specified method.

Details of the discrete wavelet transform and the fast wavelet transformation algorithm are available in many references, including Mallat (1989), Daubechies (1992), and Ogden (1997).

The inputs to the WAVFT subroutine are as follows:

data

specifies the data to transform. These data must be in either a row or column vector.

opt

refers to an options vector with the following components:

opt[1]

specifies the boundary handling used in computing the wavelet transform. At each level of the wavelet decomposition, necessary boundary scaling coefficients are obtained by extending the interior scaling coefficients at that level as follows:

opt[1]=0

specifies extension by zero.

opt[1]=1

specifies periodic extension.

opt[1]=2

specifies polynomial extension.

opt[1]=3

specifies extension by reflection.

opt[1]=4

specifies extension by anti-symmetric reflection.

opt[2]

specifies the polynomial degree that is used for polynomial extension. The value of opt[2] is ignored if opt[1].

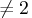opt[2]=0

specifies constant extension.

opt[2]=1

specifies linear extension.

opt[2]=2

specifies quadratic extension.

opt[3]

specifies the wavelet family.

opt[3]=1

specifies the Daubechies Extremal phase family (Daubechies, 1992).

opt[3]=2

specifies the Daubechies Least Asymmetric family (also known as the Symmlet family) (Daubechies, 1992).

opt[4]

specifies the wavelet family member. Valid values are

opt[4]=1 through 10,

if opt[3]=1

opt[4]=4 through 10,

if opt[3]=2

Some examples of wavelet specifications are

opt={1 . 1 1};

specifies the first member (more commonly known as the Haar system) of the Daubechies extremal phase family with periodic boundary handling.

opt={2 1 2 5};

specifies the fifth member of the Symmlet family with linear extension boundary handling.

levels

is an optional scalar argument that specifies the number of levels from the top level to be computed in the decomposition. If you do not specify this argument, then the decomposition terminates at level 0. Usually, you do not need to specify this optional argument. You use this option to avoid unneeded computations in situations where you are interested in only the higher level detail and scaling coefficients.

The WAVFT subroutine returns

decomp

a row vector that encapsulates the specified wavelet transform. The information that is encoded in this vector includes:

• the options specified for computing the transform
• the number of detail coefficients at each level of the decomposition
• all detail coefficients
• the scaling coefficients at the bottom level of the decomposition
• boundary scaling coefficients at all levels of the decomposition

Note: decomp is a private representation of the specified wavelet transform and is not intended to be interpreted in its raw form. Rather, you should use this vector as an input argument to the WAVIFT, WAVPRINT, WAVGET, and WAVTHRSH subroutines

The following program shows an example that uses wavelet calls to estimate and reconstruct a piecewise constant function:

  
    /* define a piecewise constant step function */ 
    start blocky(t); 
       /* positions (p) and magnitudes (h) of jumps */ 
       p = {0.1 0.13 0.15 0.23 0.25 0.4 0.44 0.65 0.76 0.78 0.81}; 
       h  = {4 -5 3 -4 5 -4.2 2.1 4.3 -3.1 2.1 -4.2}; 
  
       y=j(1, ncol(t), 0); 
       do i=1 to ncol(p); 
          diff=( (t-p[i])>=0 ); 
          y=y+h[i]*diff; 
       end; 
       return (y); 
    finish blocky; 
  
    n=2##8; 
    x=1:n; 
    x=(x-1)/n; 
    y=blocky(x); 
  
    optn = { 2, /* polynomial extension at boundary */ 
             1, /* using linear polynominal */ 
             1, /* Daubechies Extremal phase */ 
             3  /* family member 3 */ 
             }; 
  
    call wavft(decomp, y, optn); 
    call wavprint(decomp,1); /* print summary information */
 

  
    /* perform permanent thresholding */ 
    threshOpt = { 2, /* soft thresholding */ 
                  2, /* global threshold */ 
                  ., /* ignored */ 
                 -1  /* apply to all levels */ 
                  }; 
    call wavthrsh(decomp, threshOpt ); 
  
    /* request detail coefficients at level 4 */ 
    call wavget(detail4,decomp,2,4); 
  
    /* reconstruct function by using wavelets */ 
    call wavift(estimate,decomp); 
  
    errorSS=ssq(y-estimate); 
    print errorSS; 
  
                      Decomposition Summary 
  
       Decomposition Name                           DECOMP 
       Wavelet Family            Daubechies Extremal Phase 
       Family Member                                     3 
       Boundary Treatment       Recursive Linear Extension 
       Number of Data Points                           256 
       Start Level                                       0 
  
  
                             ERRORSS 
  
                            1.746E-25